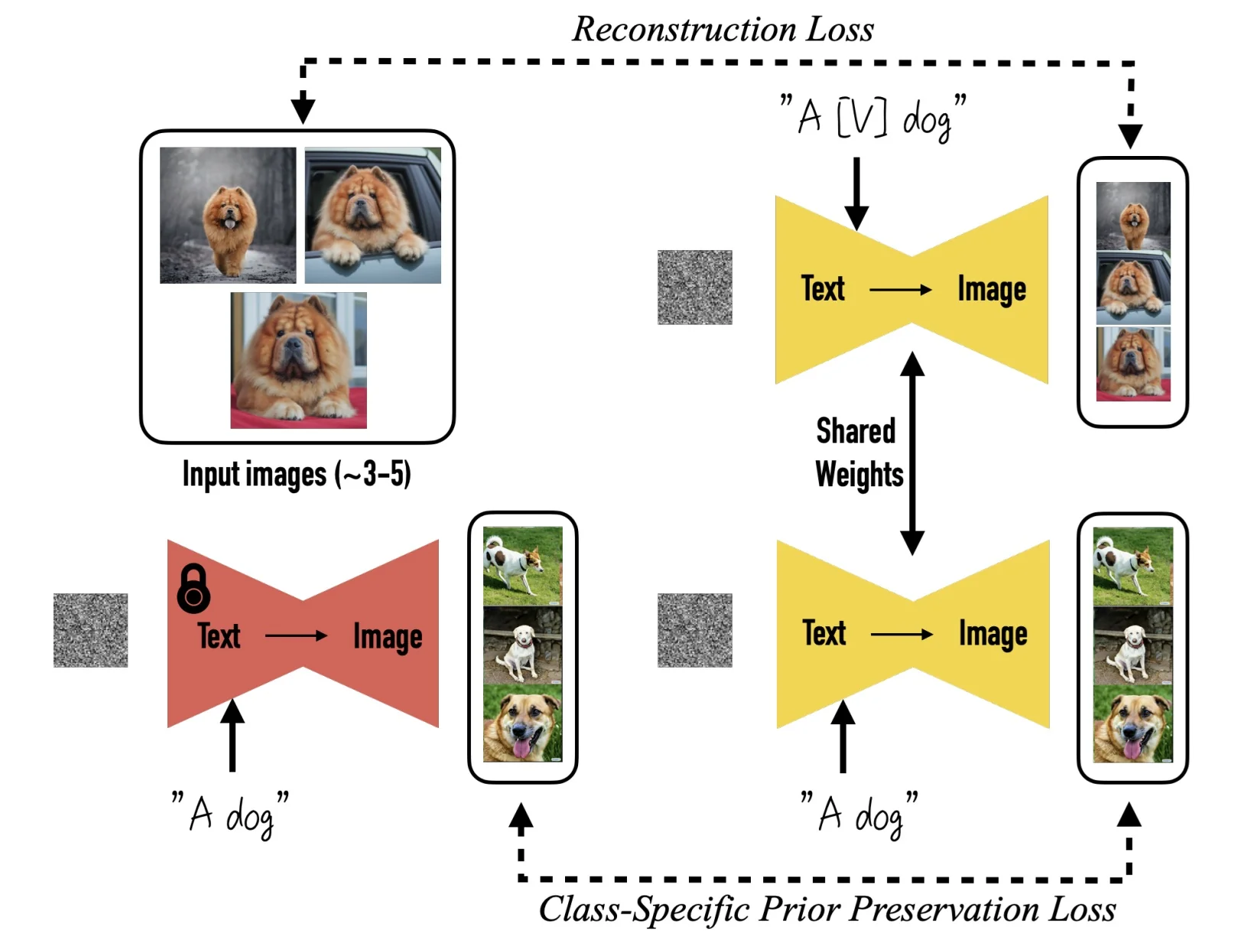
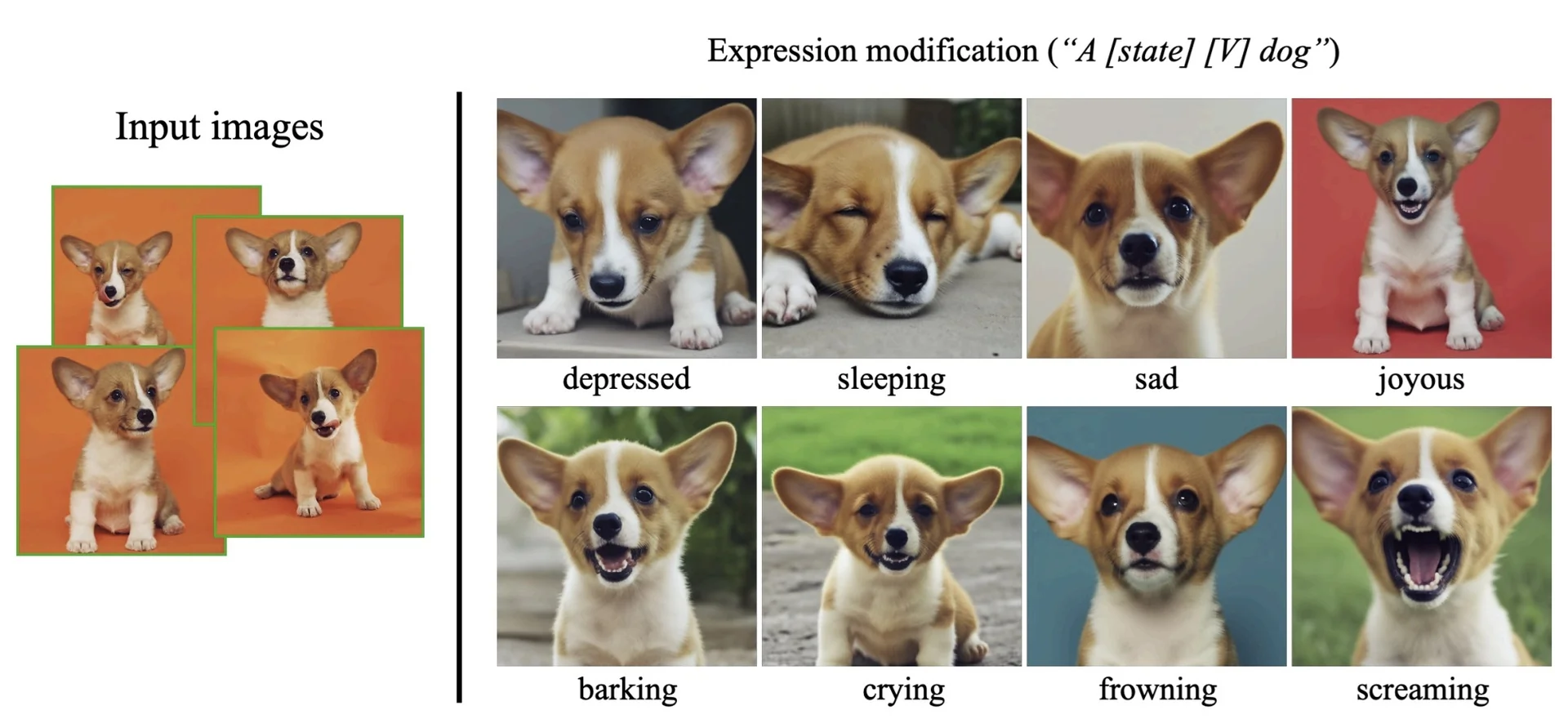
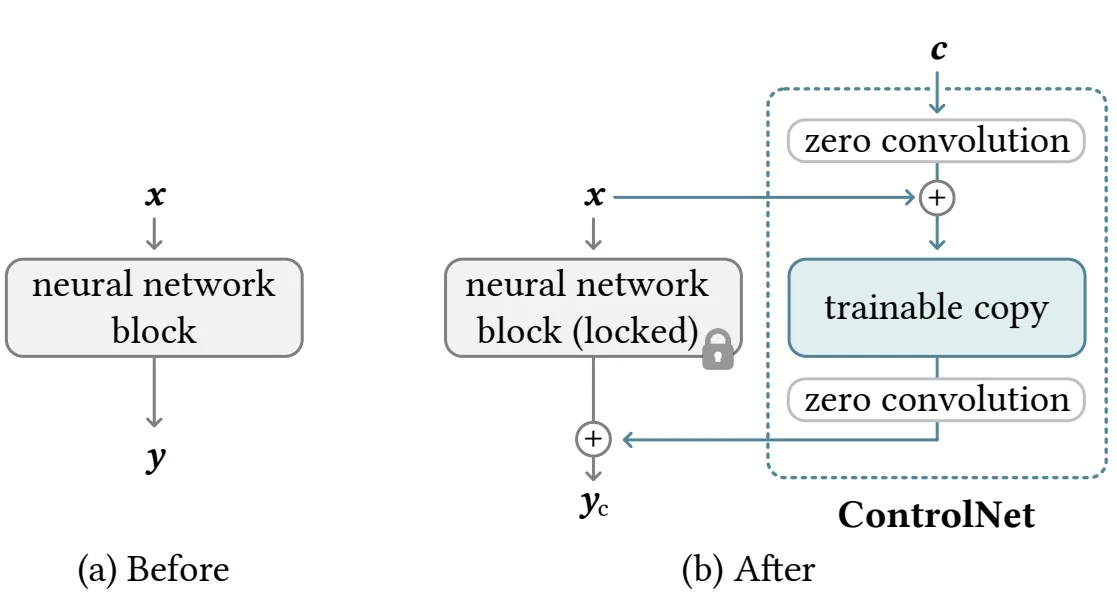
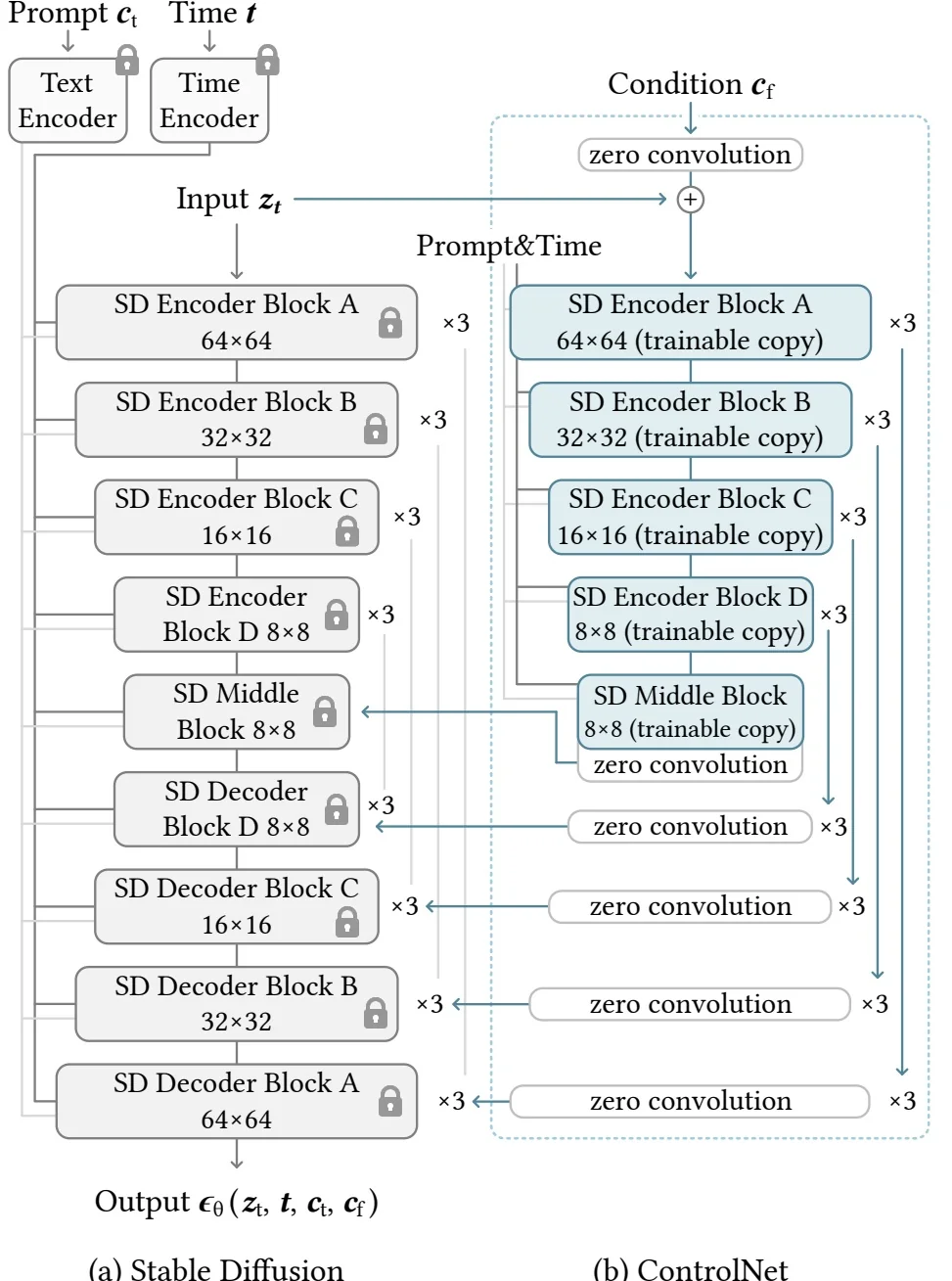
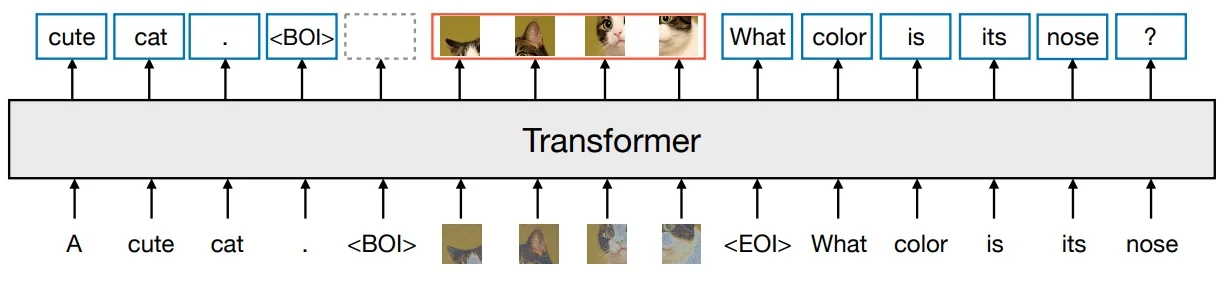
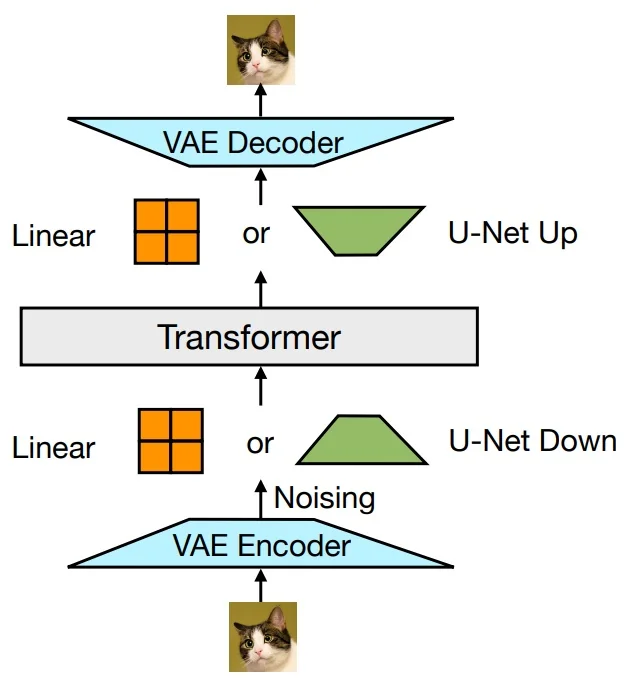
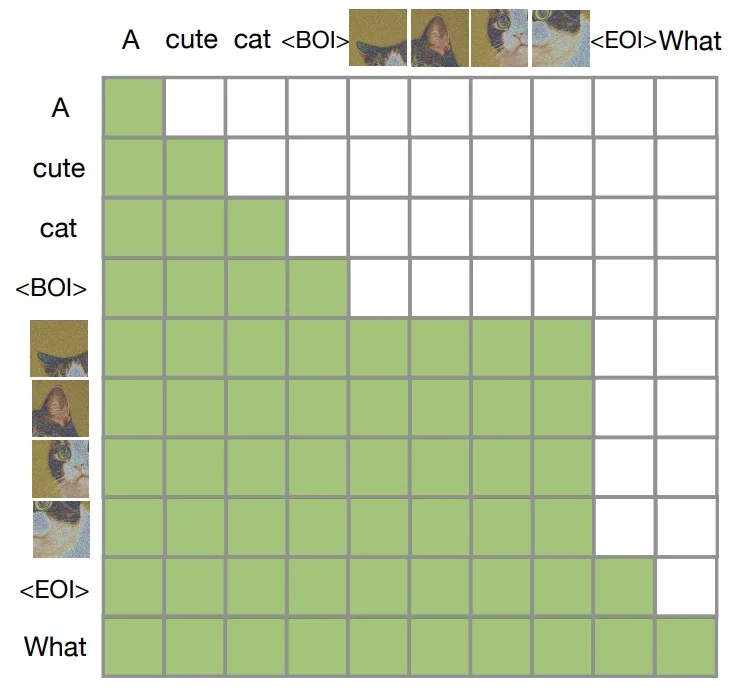
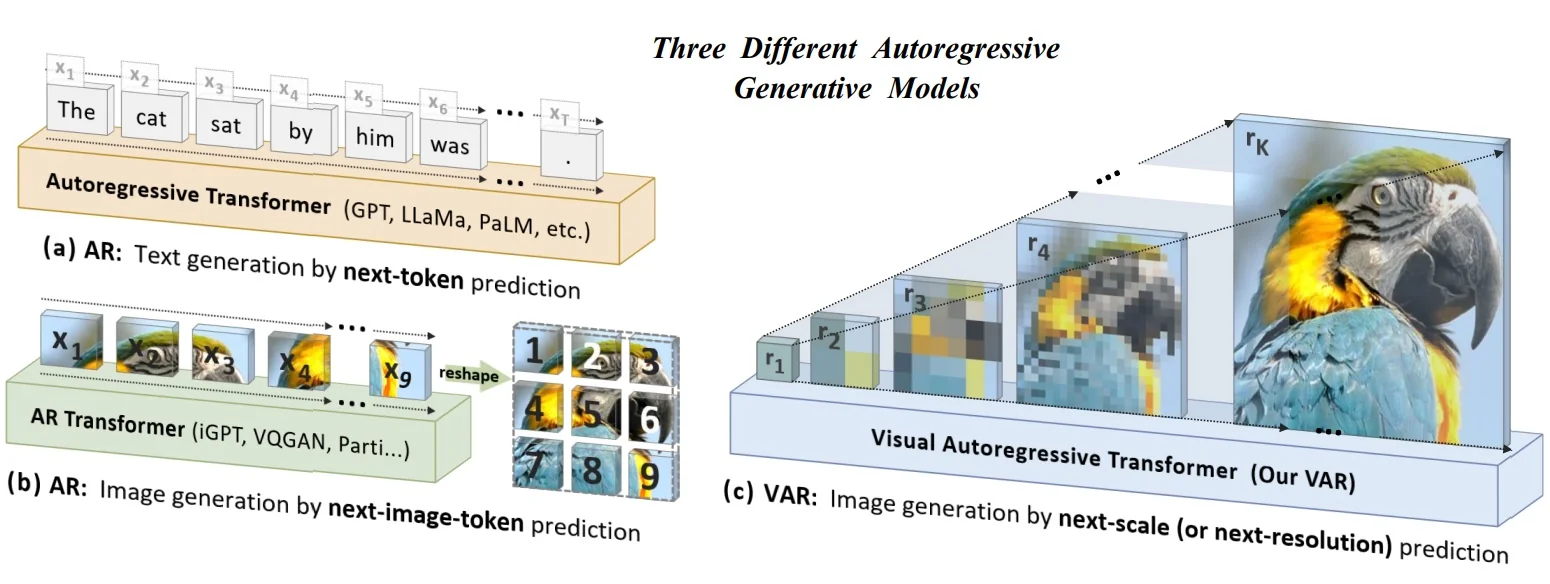
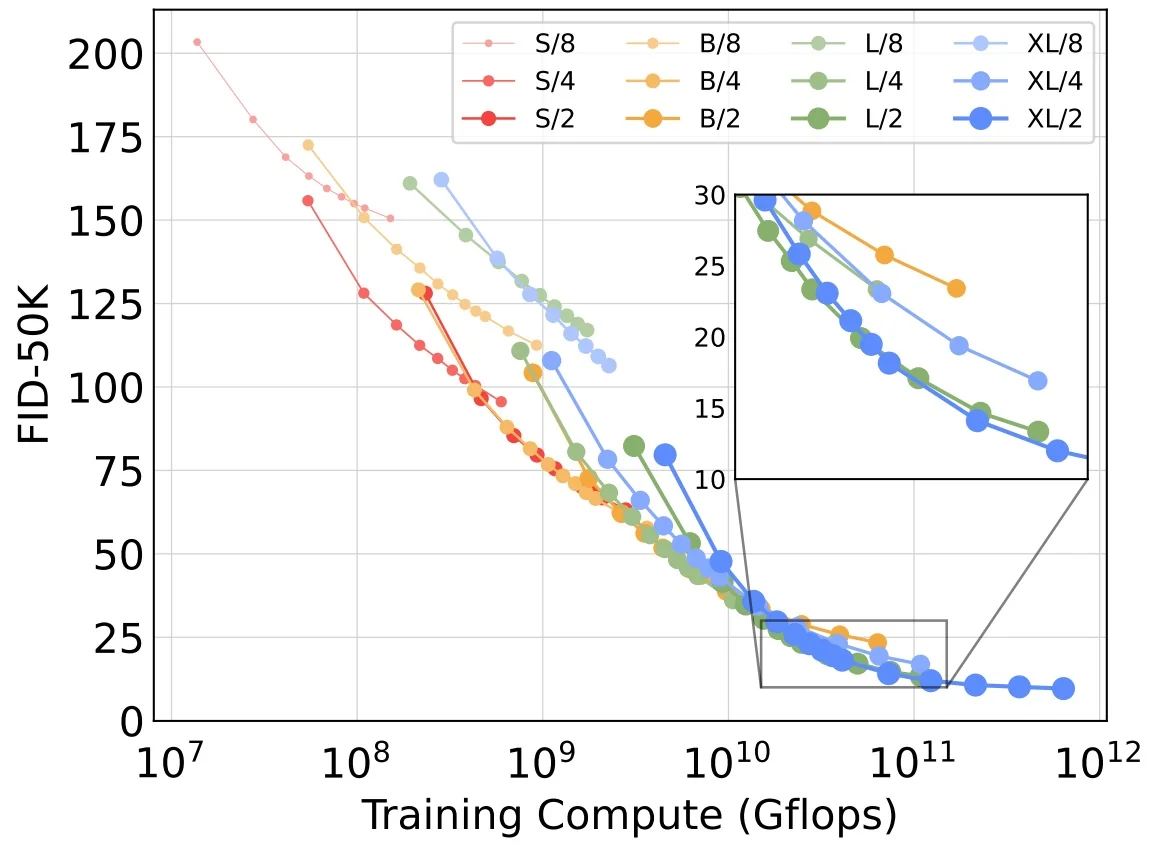
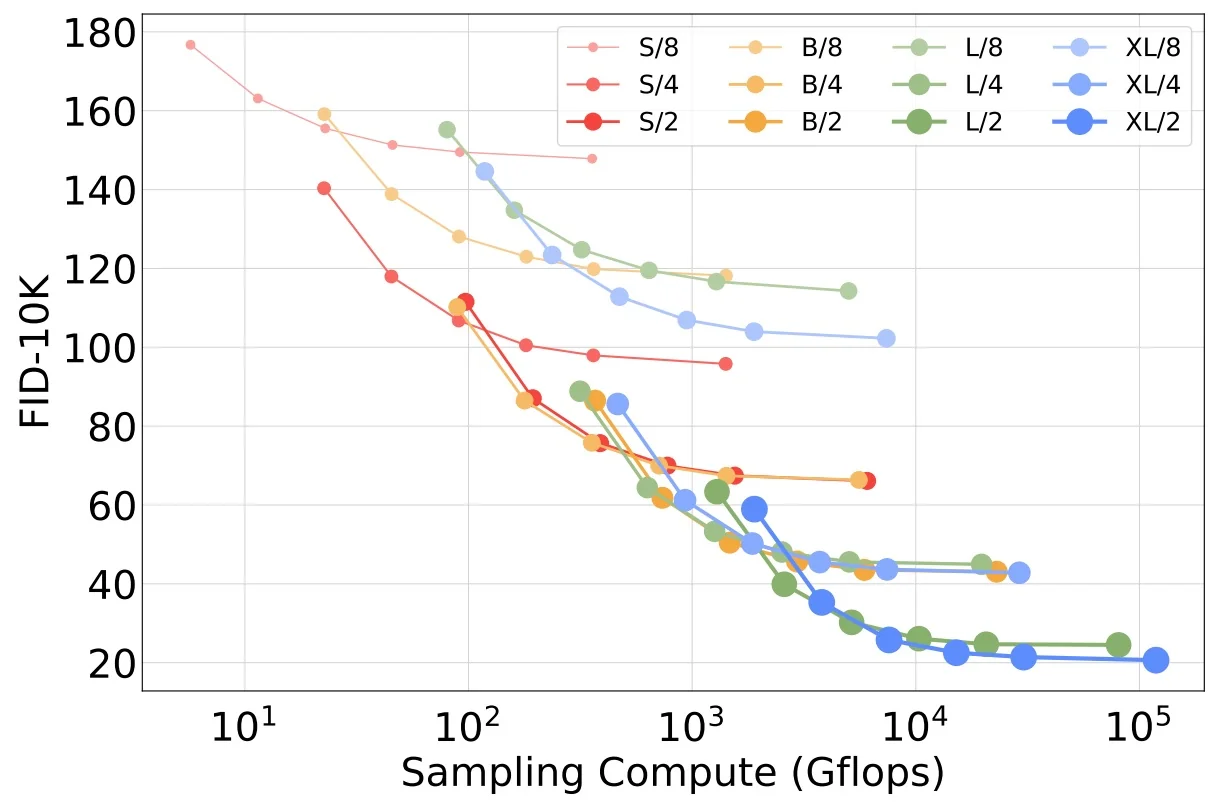
Lecture 20: Generative Models II
20.1 VAE Training and Data Generation
In the previous chapter, we introduced the Evidence Lower Bound (ELBO) as a tractable surrogate objective for training latent variable models. We now dive deeper into how this lower bound is used in practice, detailing each component of the architecture and training pipeline.
20.1.1 Encoder and Decoder Architecture: MNIST Example
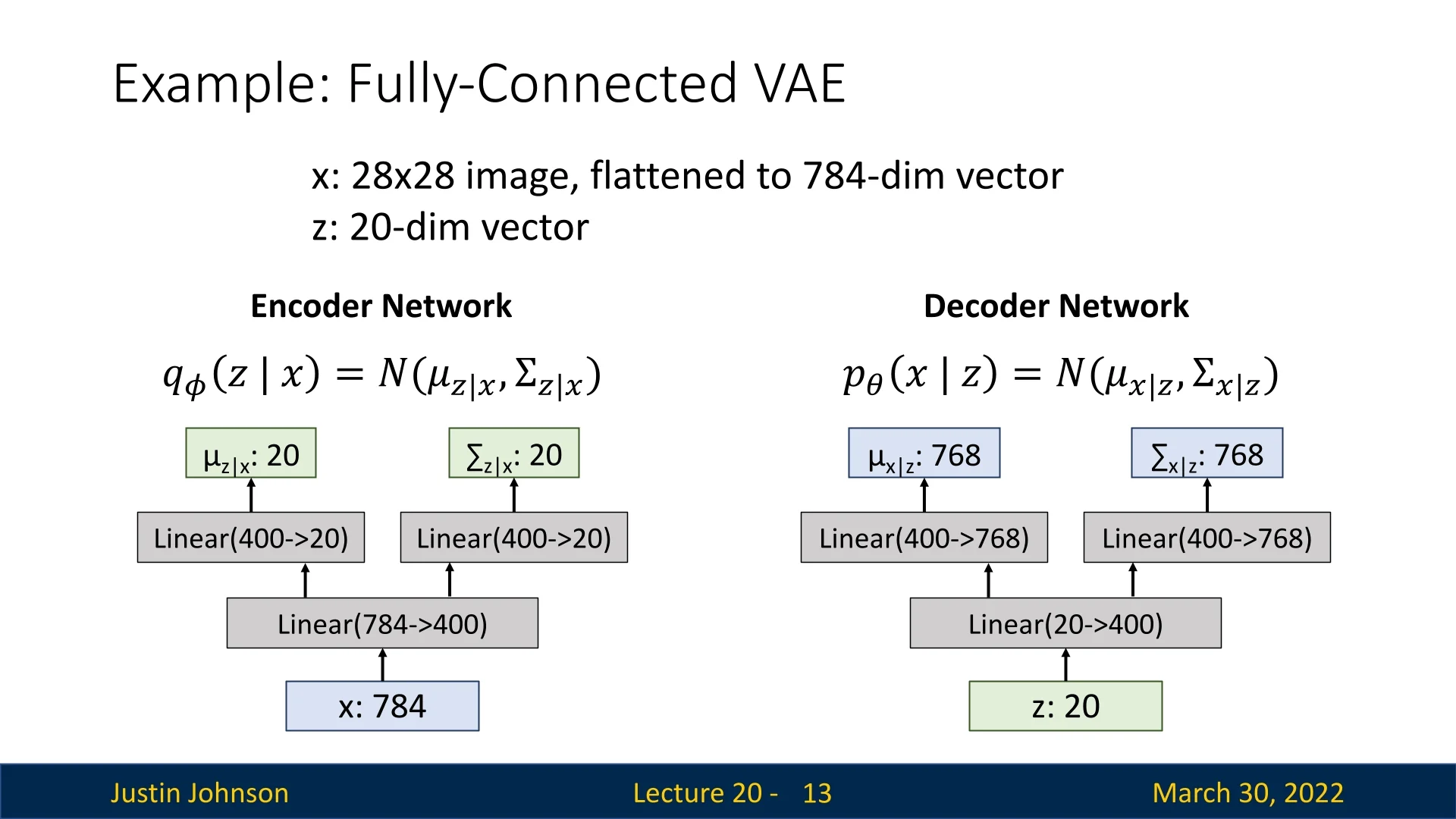
Consider training a VAE on the MNIST dataset. Each MNIST image is \(28 \times 28\) grayscale, flattened into a 784-dimensional vector \( \mathbf {x} \in \mathbb {R}^{784} \). We choose a 20-dimensional latent space \( \mathbf {z} \in \mathbb {R}^{20} \).
20.1.2 Training Pipeline: Step-by-Step
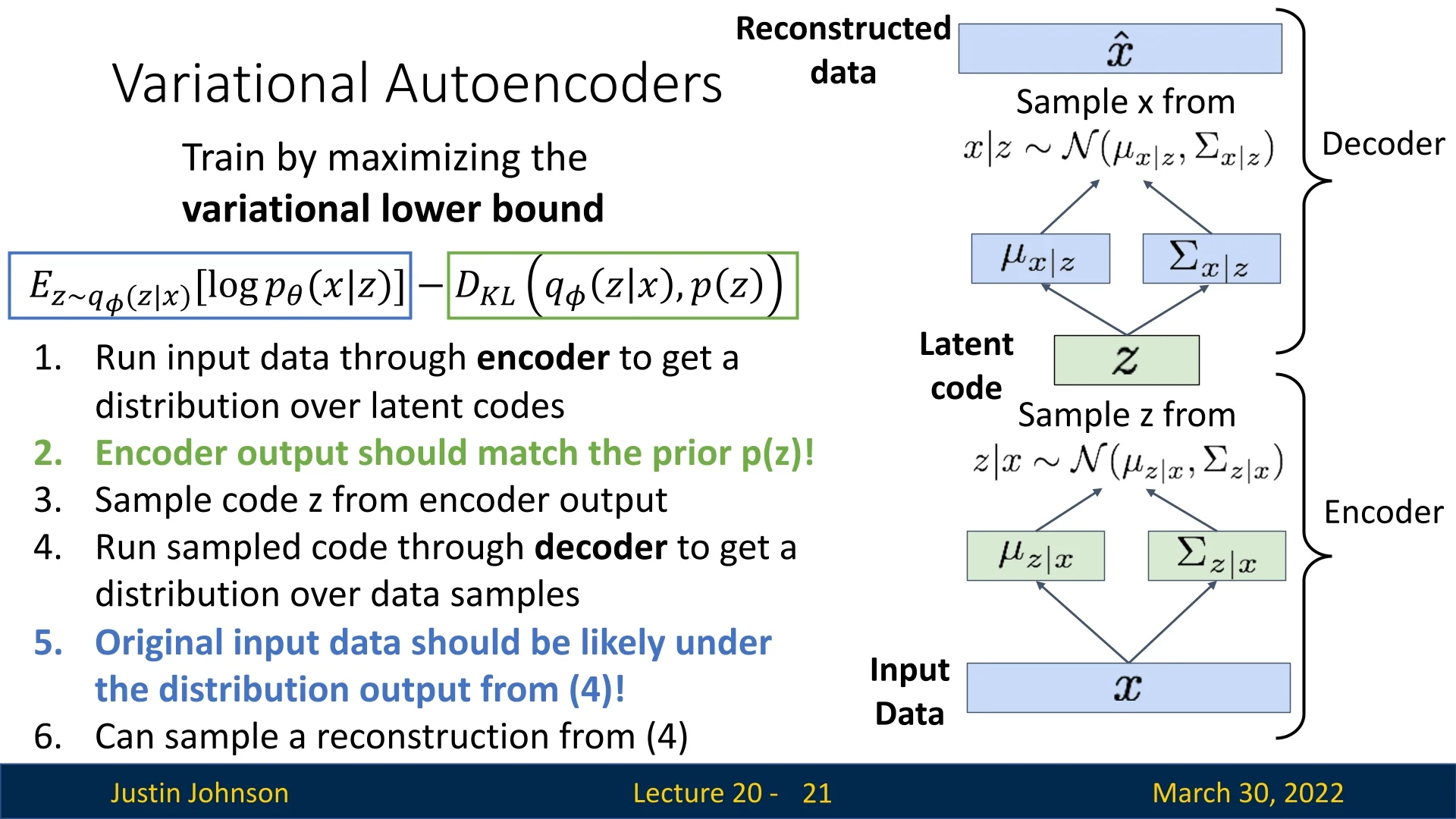
The ELBO Objective Recall from our theoretical derivation that our ultimate goal is to maximize the marginal log-likelihood of the data, \(\log p_\theta (\mathbf {x})\). However, computing this probability directly involves an intractable integral over the high-dimensional latent space. To circumvent this, we maximize a tractable surrogate objective known as the Evidence Lower Bound (ELBO):
\begin {equation} \log p_\theta (\mathbf {x}) \geq \underbrace {\mathbb {E}_{\mathbf {z} \sim q_\phi (\mathbf {z} \mid \mathbf {x})} \left [ \log p_\theta (\mathbf {x} \mid \mathbf {z}) \right ]}_{\mbox{reconstruction term}} - \underbrace {D_{\mathrm {KL}} \left (q_\phi (\mathbf {z} \mid \mathbf {x}) \,\|\, p(\mathbf {z}) \right )}_{\mbox{KL regularization}}. \label {eq:chapter20_elbo} \end {equation}
We train two neural networks simultaneously—the encoder (inference network) and the decoder (generative network)—to maximize this lower bound. Since standard deep learning frameworks (like PyTorch or TensorFlow) are designed to minimize loss functions, we formally define the VAE Loss as the negative ELBO: \begin {equation} \mathcal {L}_{\mbox{VAE}} = - \mbox{ELBO}. \label {eq:chapter20_vae_loss_def} \end {equation}
Crucial nuance: Minimizing this loss is not strictly equivalent to maximizing the true data likelihood. We are optimizing a lower bound. The gap between the log-likelihood and the ELBO is exactly the expected KL divergence between our approximate posterior and the true posterior, \(\log p_\theta (\mathbf {x}) - \mbox{ELBO} = \mathbb {E}_{\mathbf {x} \sim p_{\mbox{data}}} \left [ D_{\mathrm {KL}}\big (q_\phi (\mathbf {z} \mid \mathbf {x}) \,\|\, p_\theta (\mathbf {z} \mid \mathbf {x})\big ) \right ]\). If the encoder is not expressive enough to match the true posterior, this gap remains strictly positive. This fundamental limitation—optimizing a bound rather than the exact marginal likelihood—is one reason why later generative model families, such as diffusion models and flow-based models, explore alternative training objectives that do not rely on variational lower bounds.
For a high-level discussion on the properties of latent spaces (e.g., the manifold hypothesis), please refer back to Section Lecture 19 (Chapter 19). Below, we detail the practical execution of the VAE training pipeline in six stages.
- 1.
- Run input \( \mathbf {x} \) through the encoder.
The encoder network \( q_\phi (\mathbf {z} \mid \mathbf {x}) \) processes the input image, but unlike a standard autoencoder, it does not output a single latent code. Instead, it predicts a probability distribution over the latent space. Specifically, for a latent dimensionality \( J \), the encoder outputs two vectors: \[ \boldsymbol {\mu }_{z|x} \in \mathbb {R}^J \quad \mbox{and} \quad \boldsymbol {\sigma }^2_{z|x} \in \mathbb {R}^J \] These vectors parameterize a diagonal Gaussian distribution \( q_\phi (\mathbf {z} \mid \mathbf {x}) = \mathcal {N}(\boldsymbol {\mu }_{z|x}, \operatorname {diag}(\boldsymbol {\sigma }^2_{z|x})) \). In what follows, we will often abbreviate \(\boldsymbol {\mu }_{z|x}\) and \(\boldsymbol {\sigma }^2_{z|x}\) as \(\boldsymbol {\mu }\) and \(\boldsymbol {\sigma }^2\) for brevity.
Note on Stability: In many implementations, the encoder actually predicts log-variance, \(\log \boldsymbol {\sigma }^2\), rather than \(\boldsymbol {\sigma }^2\) directly. This improves numerical stability by mapping the variance domain \((0, \infty )\) to the real line \((-\infty , \infty )\). The variance is then recovered via an element-wise exponential.
- 2.
- Compute the KL divergence between the encoder’s
distribution and the prior.
To ensure the latent space remains well-behaved, we enforce a penalty if the encoder’s predicted distribution diverges from a fixed prior, typically the standard multivariate Gaussian \( p(\mathbf {z}) = \mathcal {N}(\mathbf {0}, \mathbf {I}) \).
Because both the posterior and prior are Gaussian, the Kullback-Leibler (KL) divergence has a convenient closed-form solution. We compute this simply by summing over all \( J \) latent dimensions: \begin {equation} D_{\mathrm {KL}}\big (q_\phi (\mathbf {z} \mid \mathbf {x}) \,\|\, p(\mathbf {z})\big ) = \frac {1}{2} \sum _{j=1}^{J} \left ( 1 + \log \sigma _j^2 - \mu _j^2 - \sigma _j^2 \right ). \label {eq:chapter20_vae_kl_closed_form} \end {equation} This term acts as a regularizer. It pulls the mean \( \boldsymbol {\mu } \) towards 0 and the variance \( \boldsymbol {\sigma }^2 \) towards 1. Without this term, the encoder could ”cheat” by clustering data points far apart (making \( \mu \) huge) or by shrinking the variance to effectively zero (making \( \sigma \to 0 \)), effectively collapsing the VAE back into a standard deterministic autoencoder.
- 3.
- Sample latent code \( \mathbf {z} \) using the Reparameterization Trick.
The decoder requires a concrete vector \( \mathbf {z} \) to generate an output. Therefore, we must sample from the distribution defined by \( \boldsymbol {\mu } \) and \( \boldsymbol {\sigma } \).
The Obstacle (Blocking Gradients): A naive sampling operation breaks the computation graph. Backpropagation requires continuous derivatives, but we cannot differentiate with respect to a random roll of the dice. If we simply sampled \( z \), the gradient flow would stop at the sampling node.
The Solution (Reparameterization): We use the reparameterization trick to bypass this block. We express \( \mathbf {z} \) as a deterministic transformation of the encoder parameters and an auxiliary noise source: \begin {equation} \mathbf {z} = \boldsymbol {\mu }_{z|x} + \boldsymbol {\sigma }_{z|x} \odot \boldsymbol {\epsilon }, \quad \boldsymbol {\epsilon } \sim \mathcal {N}(\mathbf {0}, \mathbf {I}). \label {eq:chapter20_vae_reparameterization} \end {equation} Practical Implementation Details:
- Source of Randomness: We sample a noise vector \(\boldsymbol {\epsilon } \in \mathbb {R}^J\) from \(\mathcal {N}(\mathbf {0}, \mathbf {I})\). This variable effectively ”holds” the stochasticity.
- Vectorization: In practice, we sample a unique \( \boldsymbol {\epsilon } \) for every data point in the batch during every forward pass.
- Gradient Flow: The operation \( \odot \) denotes element-wise multiplication. Crucially, because \( \boldsymbol {\epsilon } \) is treated as an external constant during the backward pass, gradients can flow freely through \( \boldsymbol {\mu } \) and \( \boldsymbol {\sigma } \) back to the encoder weights.
For a visual walkthrough of this mechanism, we recommend:
ML&DL Explained { Reparameterization Trick. - 4.
- Feed the sampled latent code \( \mathbf {z} \) into the decoder.
The decoder \( p_\theta (\mathbf {x} \mid \mathbf {z}) \) maps the sampled code \( \mathbf {z} \) back to the high-dimensional data space. It outputs the parameters of the likelihood distribution for the pixels (e.g., the predicted mean intensity for each pixel).
- 5.
- Evaluate the reconstruction likelihood.
We measure how well the decoder ”explains” the original input \( \mathbf {x} \) given the sampled code \( \mathbf {z} \). For real-valued images, we typically assume a factorized Gaussian likelihood with fixed variance. In this case, maximizing the log-likelihood is equivalent (up to an additive constant) to minimizing the squared \(\ell _2\) reconstruction error: \begin {equation} \mathcal {L}_{\mbox{recon}} \,\propto \, \left \| \mathbf {x} - \hat {\mathbf {x}} \right \|_2^2. \label {eq:chapter20_vae_recon_mse} \end {equation}
- 6.
- Combine terms to compute the total VAE Loss.
The final objective function is the sum of the reconstruction error and the regularization penalty: \begin {equation} \mathcal {L}_{\mbox{VAE}}(\mathbf {x}) = \underbrace {- \mathbb {E}_{\mathbf {z} \sim q_\phi (\mathbf {z} \mid \mathbf {x})} \left [\log p_\theta (\mathbf {x} \mid \mathbf {z})\right ]}_{\mbox{reconstruction loss}} + \underbrace {D_{\mathrm {KL}}\big (q_\phi (\mathbf {z} \mid \mathbf {x}) \,\|\, p(\mathbf {z})\big )}_{\mbox{regularization loss}}. \label {eq:chapter20_vae_total_loss} \end {equation}
The VAE “Tug-of-War” (Regularization vs. Reconstruction):
The VAE objective function creates a fundamental conflict between two opposing goals, forcing the model to find a useful compromise:
- The Reconstruction Term (Distinctness):
-
This term maximizes \(\mathbb {E}[\log p_\theta (\mathbf {x} \mid \mathbf {z})]\). It drives the encoder to be as precise as possible to minimize error. The Extreme Case: If left unchecked, the encoder would reduce the variance to zero (\(\sigma \to 0\)). The latent distribution would collapse into a Dirac delta function (a single point), effectively turning the VAE into a standard deterministic Autoencoder. While this minimizes reconstruction error, the model effectively “memorizes” the training data as isolated points, failing to learn the smooth, continuous manifold required for generating new images.
- The KL Term (Smoothness):
-
This term minimizes \(D_{\mathrm {KL}}(q_\phi (\mathbf {z} \mid \mathbf {x}) \,\|\, p(\mathbf {z}))\). It forces the encoder’s output to match the standard Gaussian prior (\(\mathcal {N}(0, I)\)), encouraging posteriors to be “noisy” and overlap. The Extreme Case: If left unchecked (i.e., if this regularization dominates), the encoder will ignore the input \(\mathbf {x}\) entirely to satisfy the prior perfectly. This phenomenon, known as Posterior Collapse, results in latent codes that contain no information about the input image, causing the decoder to output generic noise or average features regardless of the input.
The Result: This tension prevents the model from memorizing exact coordinates (Autoencoder) while preventing it from outputting pure noise (Posterior Collapse). The VAE settles on a “cloud-like” representation that is distinct enough to preserve content but smooth enough to allow for interpolation and generation.
Why a Diagonal Gaussian Prior?
We typically choose the prior \( p(\mathbf {z}) \) to be a unit Gaussian \( \mathcal {N}(\mathbf {0}, \mathbf {I}) \). While simple, this choice provides powerful benefits:
- Analytical Tractability: As seen in Equation 20.3, the KL divergence between two Gaussians can be computed without expensive sampling or integrals.
- Encouraging Disentanglement: The diagonal covariance structure assumes independence between dimensions. This biases the model towards allocating distinct generative factors to separate dimensions (e.g., “azimuth” vs. “elevation”) rather than entangling them, although in practice such disentanglement is not guaranteed.
- Manifold Smoothness: By forcing the posterior to overlap with the standard normal prior, we prevent the model from memorizing the training set (which would look like a set of isolated delta functions). Instead, the model learns a smooth, continuous manifold where any point sampled from \( \mathcal {N}(\mathbf {0}, \mathbf {I}) \) is likely to decode into a plausible image.
20.1.3 How Can We Generate Data Using VAEs?
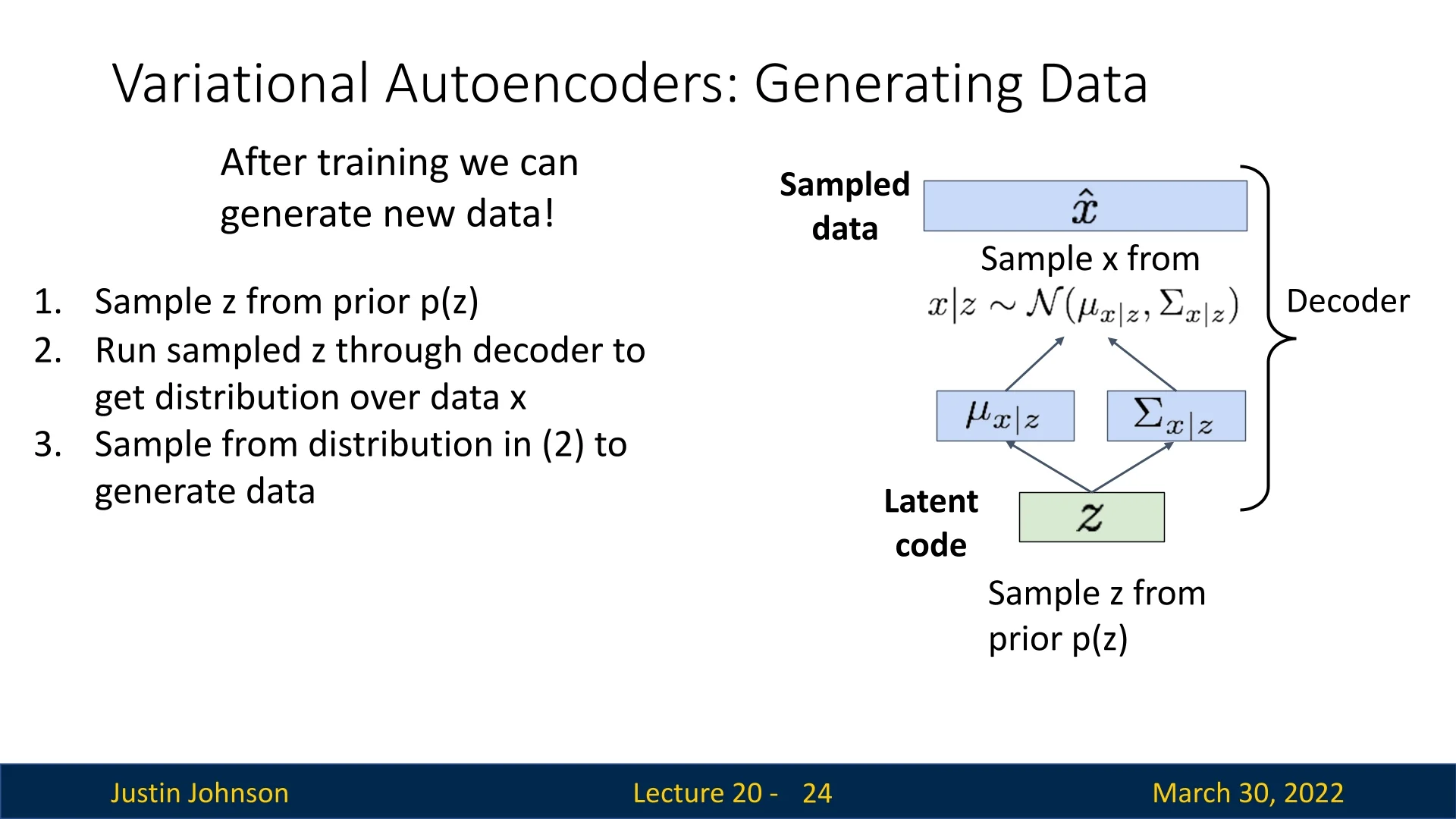
Once a Variational Autoencoder is trained, we can use it as a generative model to produce new data samples. Unlike the training phase, which starts from observed inputs \( \mathbf {x} \), the generative process starts from the latent space.
Sampling Procedure To generate a new data point (e.g., a novel image), we follow a simple three-step process:
- 1.
- Sample a latent code \( \mathbf {z} \sim p(\mathbf {z}) \).
This draws from the prior distribution, which is typically set to \( \mathcal {N}(\mathbf {0}, \mathbf {I}) \). The latent space has been trained such that this prior corresponds to plausible latent factors of variation. - 2.
- Run the sampled \( \mathbf {z} \) through the decoder \( p_\theta (\mathbf {x} \mid \mathbf {z}) \).
This yields the parameters (e.g., mean and variance) of a probability distribution over possible images. - 3.
- Sample a new data point \( \hat {\mathbf {x}} \) from this output distribution.
Typically, we sample from the predicted Gaussian: \[ \hat {\mathbf {x}} \sim \mathcal {N}(\boldsymbol {\mu }_{x|z}, \operatorname {diag}(\boldsymbol {\sigma }^2_{x|z})) \] In some applications (e.g., grayscale image generation), one might use just the mean \( \boldsymbol {\mu }_{x|z} \) as the output.
This process enables the generation of diverse and novel data samples that resemble the training distribution, but are not copies of any specific training point.
20.2 Results and Applications of VAEs
Variational Autoencoders not only enable data generation but also support rich latent-space manipulation. Below, we summarize key empirical results and capabilities demonstrated in foundational works.
20.2.1 Qualitative Generation Results
Once trained, VAEs can generate samples that resemble the training data distribution. For instance:
- On CIFAR-10, generated samples are 32×32 RGB images with recognizable textures and object-like patterns.
- On the Labeled Faces in the Wild (LFW) dataset, VAEs generate realistic human faces, capturing high-level structures such as symmetry, eyes, hair, and pose.
20.2.2 Latent Space Traversals and Image Editing
Once a VAE has been trained, we are no longer limited to simply reconstructing inputs. Because the latent prior \(p(\mathbf {z})\) is typically chosen to be a diagonal Gaussian, the model assumes that different coordinates of \(\mathbf {z}\) are a priori independent. This structural assumption makes it natural to manipulate individual latent dimensions and observe how specific changes in the code \(\mathbf {z}\) manifest in the generated data.
Example 1: MNIST Morphing A classic illustration of this property is provided by [292] using the MNIST dataset of handwritten digits. By training a VAE with a strictly two-dimensional latent space, we can visualize the learned manifold by systematically varying the latent variables \( z_1 \) and \( z_2 \) across a regular grid (using the inverse CDF of the Gaussian to map the grid to probability mass) and decoding the results.
As shown in the below figure, this reveals a highly structured and continuous latent space. Rather than jumping randomly between digits, the decoder produces smooth semantic interpolations:
- Vertical Morphing (\( z_1 \)): Moving along the vertical axis transforms the digit identity smoothly. For instance, we can observe a 6 morphing into a 9, which then transitions into a 7. With slight variations in \( z_2 \), this path may also pass through a region decoding to a 2.
- Horizontal Morphing (\( z_2 \)): Moving along the horizontal axis produces different transitions. In some regions, a 7 gradually straightens into a 1. In others, a 9 thickens into an 8, loops into a 3, and settles back into an 8.
This confirms that the VAE has learned a smooth, continuous manifold where nearby latent codes decode to visually similar images, and linear interpolation in latent space corresponds to meaningful semantic morphing.
The General Editing Pipeline We can generalize this “traversal” idea into a simple but powerful pipeline for semantic image editing. As illustrated in the below figure, the process is:
- 1.
- Encode: Run the input image \( \mathbf {x} \) through the encoder to obtain the approximate posterior \( q_\phi (\mathbf {z} \mid \mathbf {x}) \).
- 2.
- Sample: Draw a latent code \( \mathbf {z} \sim q_\phi (\mathbf {z} \mid \mathbf {x}) \) using the reparameterization trick from Section 20.1.2.
- 3.
- Edit in latent space: Manually modify one or more coordinates of \( \mathbf {z} \) (for example, set \( \tilde {z}_j = z_j + \delta \)) to obtain a modified code \( \tilde {\mathbf {z}} \).
- 4.
- Decode: Pass the modified code \( \tilde {\mathbf {z}} \) through the decoder \( p_\theta (\mathbf {x} \mid \mathbf {z}) \) to obtain the parameters of an edited-image distribution \( p_\theta (\mathbf {x} \mid \tilde {\mathbf {z}}) \).
- 5.
- Visualize: Either sample \( \hat {\mathbf {x}} \sim p_\theta (\mathbf {x} \mid \tilde {\mathbf {z}}) \) or directly visualize the decoder’s mean as the edited image.
In other words, the encoder maps images to a “control space” (latent codes), we apply simple algebraic edits there, and the decoder renders the results back into image space.
Example 2: Disentanglement in Faces While MNIST mainly exhibits simple geometric morphing, VAEs applied to more complex data often uncover high-level semantic attributes. This phenomenon is known as disentanglement: particular dimensions of \( \mathbf {z} \) align with individual generative factors.
In the original VAE paper [292], the authors demonstrated this on the Frey Face dataset. Even without label supervision, the model discovered latent coordinates that separately control expression and pose:
- Varying one latent coordinate continuously changes the degree of smiling.
- Varying another coordinate continuously changes the head pose.
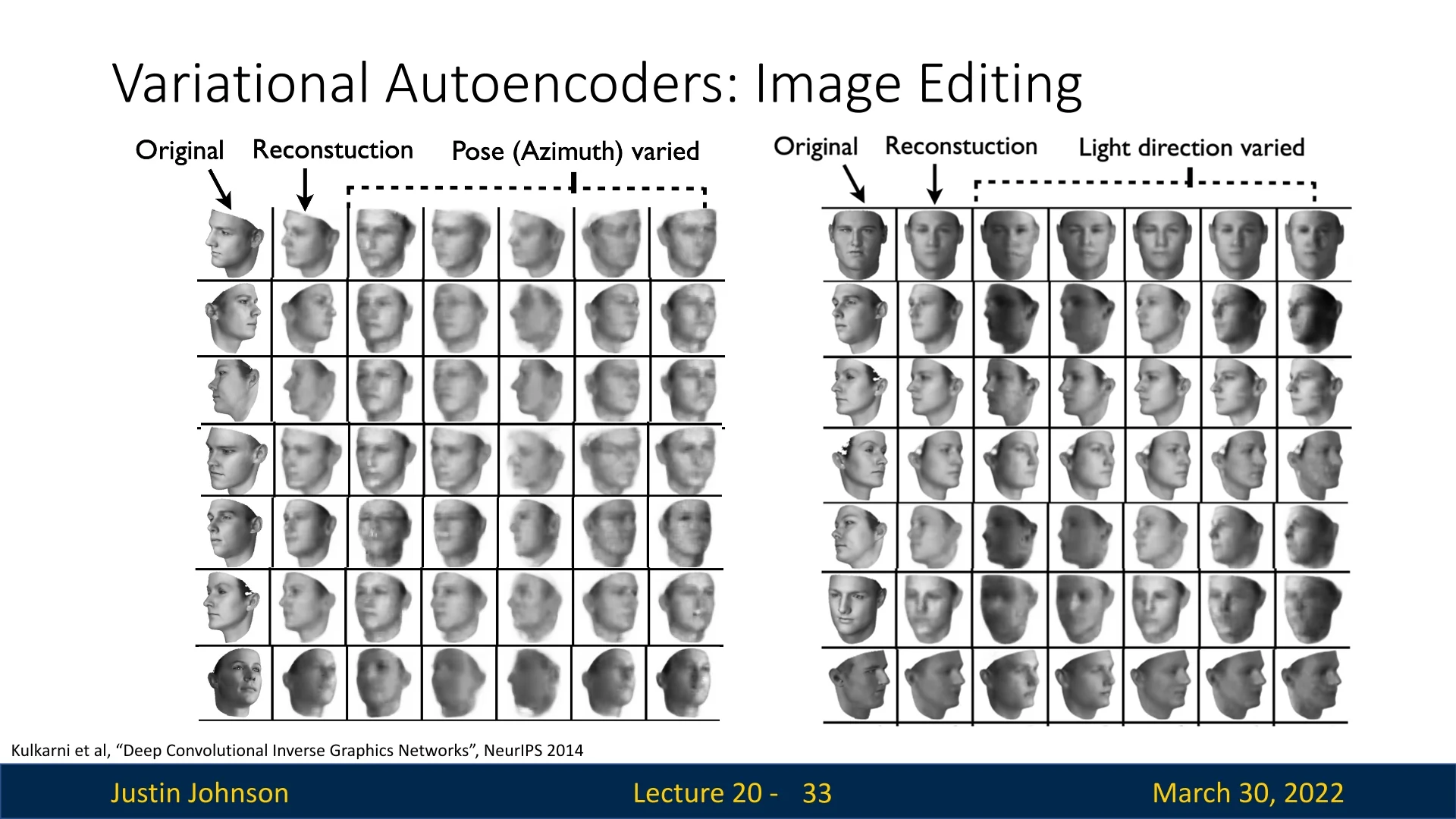
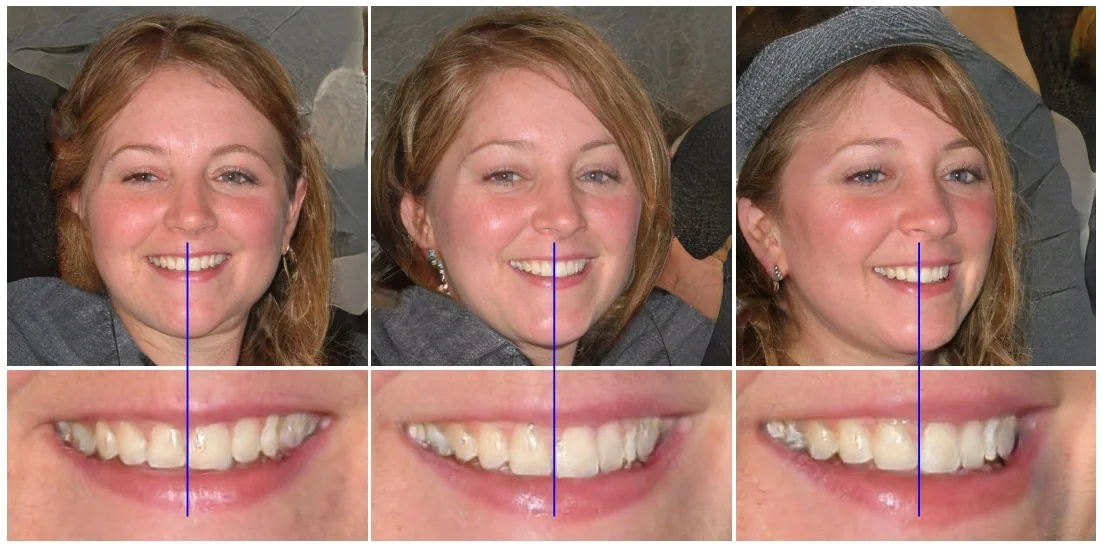
This capability was further refined by [308] in the Deep Convolutional Inverse Graphics Network (DC-IGN). Training on 3D-rendered faces, they identified specific latent variables that act like “knobs” in a graphics engine:
- Pose (azimuth): rotating the head around the vertical axis while preserving identity.
- Lighting: moving the light source around the subject, while keeping pose fixed.
As shown in the following figure, editing a single latent value can rotate a face in 3D or sweep the illumination direction, indicating that the model has captured underlying 3D structure from 2D pixels.
These examples highlight a key qualitative advantage of VAEs: beyond modeling the data distribution, they expose a low-dimensional latent space in which many generative factors can be probed, interpolated, and edited. In practice, disentanglement is imperfect and not guaranteed, but even partially disentangled latents already enable powerful and interpretable control over generated images.
Takeaway Unlike autoregressive models (e.g., PixelCNN) that only model \(p(\mathbf {x})\) directly and provide no explicit latent code, VAEs learn a structured latent representation \( \mathbf {z} \). This representation can be used to interpolate between images, explore variations along semantic directions, and perform targeted edits, making VAEs particularly valuable for representation learning and controllable generation.
20.3 Summary & Examples: Variational Autoencoders
Variational Autoencoders (VAEs) introduce a probabilistic framework on top of the traditional autoencoder architecture. Instead of learning a deterministic mapping, they:
- treat the latent code \( \mathbf {z} \) as a random variable drawn from an encoder-predicted posterior \( q_\phi (\mathbf {z} \mid \mathbf {x}) \),
- model the data generation process via a conditional likelihood \( p_\theta (\mathbf {x} \mid \mathbf {z}) \),
- and optimize the Evidence Lower Bound (ELBO) instead of the intractable marginal likelihood \( p_\theta (\mathbf {x}) \).
- Principled formulation: VAEs are grounded in Bayesian inference and variational methods, giving a clear probabilistic interpretation of both training and inference.
- Amortized inference: The encoder \( q_\phi (\mathbf {z} \mid \mathbf {x}) \) allows fast, single-pass inference of latent codes for new data, which can be reused for downstream tasks such as classification, clustering, or editing.
- Interpretable latent space: As seen in the traversals above, the latent space often captures semantic factors (pose, light, expression) in a smooth, continuous manifold.
- Fast sampling: Generating new data is efficient: sample \( \mathbf {z} \sim \mathcal {N}(\mathbf {0}, \mathbf {I}) \) and decode once.
- Approximation gap: VAEs maximize a lower bound (ELBO), not the exact log-likelihood. If the approximate posterior \( q_\phi (\mathbf {z} \mid \mathbf {x}) \) is too restricted (for example, diagonal Gaussian), the model may underfit and assign suboptimal likelihood to the data.
- Blurry samples: With simple factorized Gaussian decoders (and the associated MSE-like reconstruction loss), VAEs tend to produce over-smoothed images that lack the sharp, high-frequency details achieved by PixelCNNs, GANs, or diffusion models.
Active Research Directions Research on VAEs often focuses on mitigating these downsides while preserving their strengths:
- Richer posteriors: Replacing the diagonal Gaussian \( q_\phi (\mathbf {z} \mid \mathbf {x}) \) with more flexible families such as normalizing flows or autoregressive networks to reduce the ELBO gap.
- Structured priors: Using hierarchical or discrete/categorical priors and structured latent spaces to better capture factors of variation and induce disentanglement.
- Hybrid models: Combining VAEs with autoregressive decoders (e.g., PixelVAE), so that the global structure is captured by \( \mathbf {z} \) while local detail is modeled autoregressively.
Comparison: Autoregressive vs. Variational Throughout this chapter, we have contrasted two major families of generative models. Figure 20.9 summarizes the trade-offs:
-
Autoregressive models (PixelRNN / PixelCNN):
- Directly maximize \( p_\theta (\mathbf {x}) \) with exact likelihood.
- Produce sharp, high-quality images.
- Are typically slow to sample from, since pixels are generated sequentially.
- Do not expose an explicit low-dimensional latent code.
-
Variational models (VAEs):
- Maximize a lower bound on \( p_\theta (\mathbf {x}) \) rather than the exact likelihood.
- Often produce smoother (blurrier) images with simple decoders.
- Are very fast to sample from once trained.
- Learn rich, editable latent codes that support interpolation and semantic control.
This comparison naturally raises the next question we will address: Can we combine these approaches and obtain the best of both worlds?
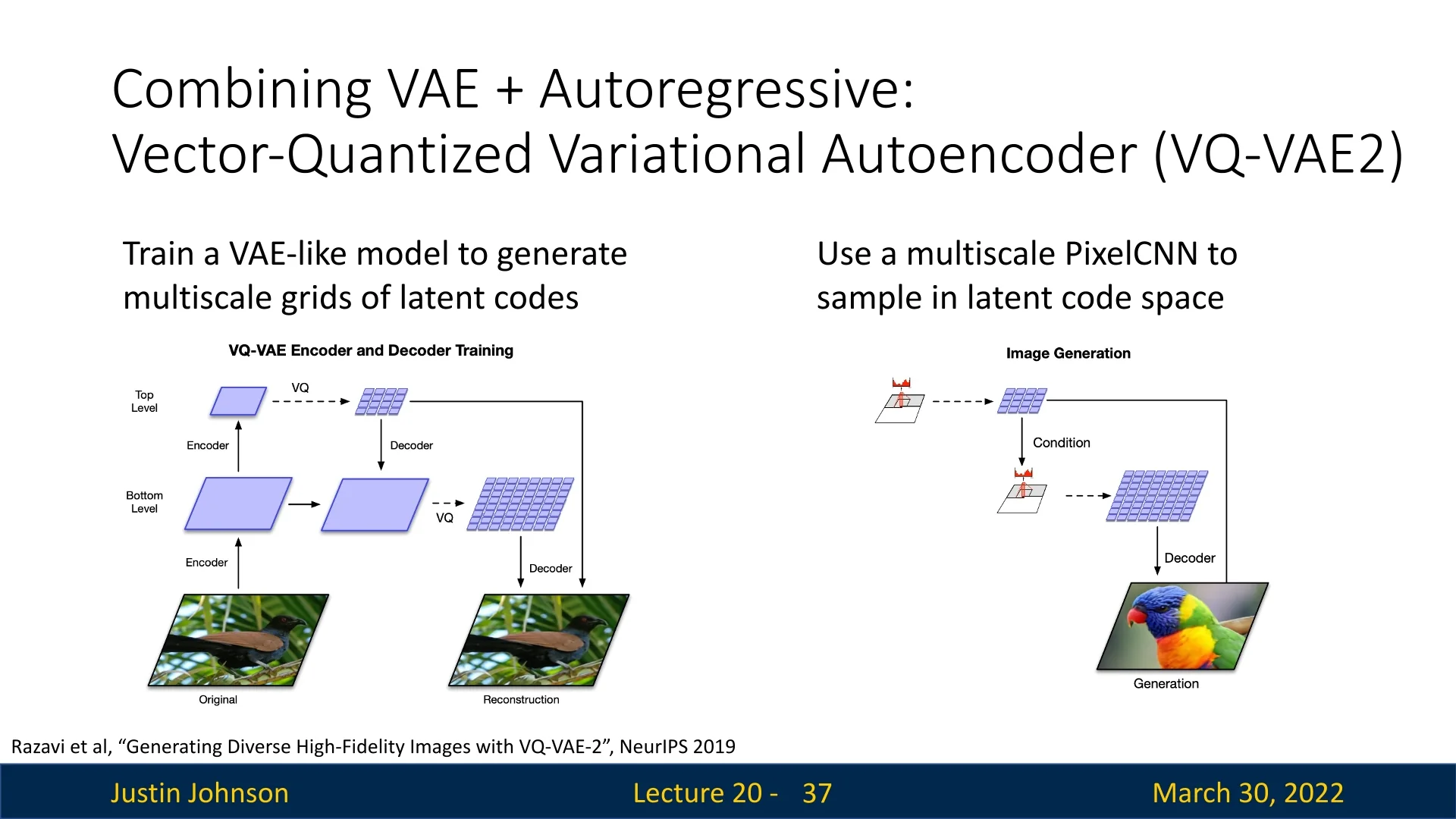
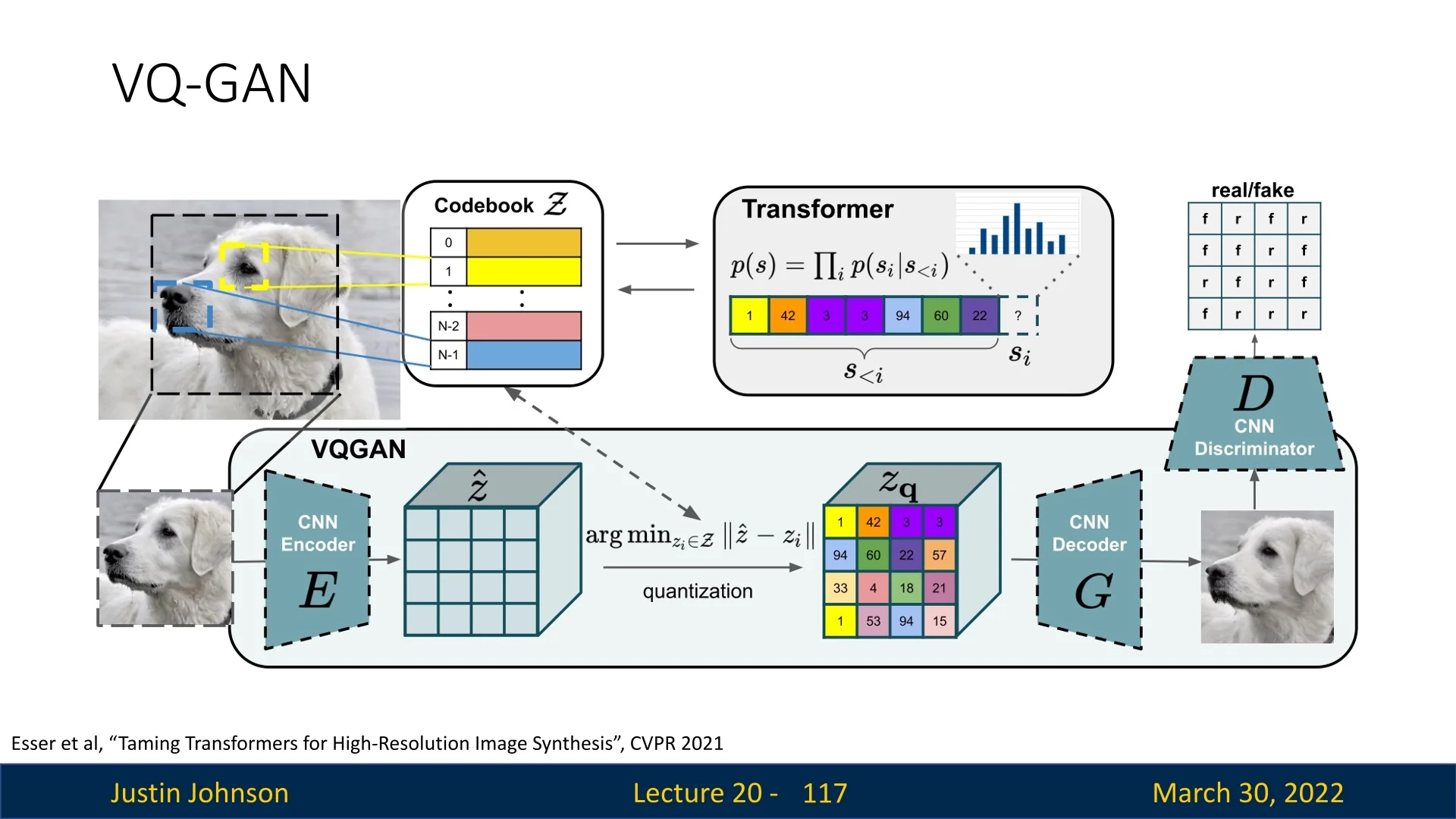
20.3.1 VQ-VAE-2: Combining VAEs with Autoregressive Models
Motivation Variational Autoencoders (VAEs) offer a principled latent variable framework for generative modeling, but their outputs often lack detail due to oversimplified priors and decoders. In contrast, autoregressive models such as PixelCNN produce sharp images by modeling pixel-level dependencies but lack interpretable latent variables and are slow to sample from.
VQ-VAE-2 [514] combines these paradigms: it learns discrete latent representations via vector quantization (as in VQ-VAE), and models their distribution using powerful autoregressive priors. This approach achieves both high-fidelity synthesis and efficient, structured latent codes.
Architecture Overview VQ-VAE-2 introduces a powerful combination of hierarchical encoding, discrete latent representations, and autoregressive priors. At its core, it improves upon traditional VAEs by replacing continuous latent variables with discrete codes through a process called vector quantization.
-
Hierarchical Multi-Level Encoder:
The input image \( \mathbf {x} \in \mathbb {R}^{H \times W \times C} \) is passed through two stages of convolutional encoders:
- A bottom-level encoder extracts a latent feature map \( \mathbf {z}_b^e \in \mathbb {R}^{H_b \times W_b \times d} \), where \( H_b < H \), \( W_b < W \). This captures low-level image details (e.g., textures, edges).
- A top-level encoder is then applied to \( \mathbf {z}_b^e \), producing \( \mathbf {z}_t^e \in \mathbb {R}^{H_t \times W_t \times d} \), with \( H_t < H_b \), \( W_t < W_b \). This higher-level map captures global semantic information (e.g., layout, object presence).
The spatial resolution decreases at each stage due to strided convolutions, forming a coarse-to-fine hierarchy of latent maps.
-
Vector Quantization and Codebooks:
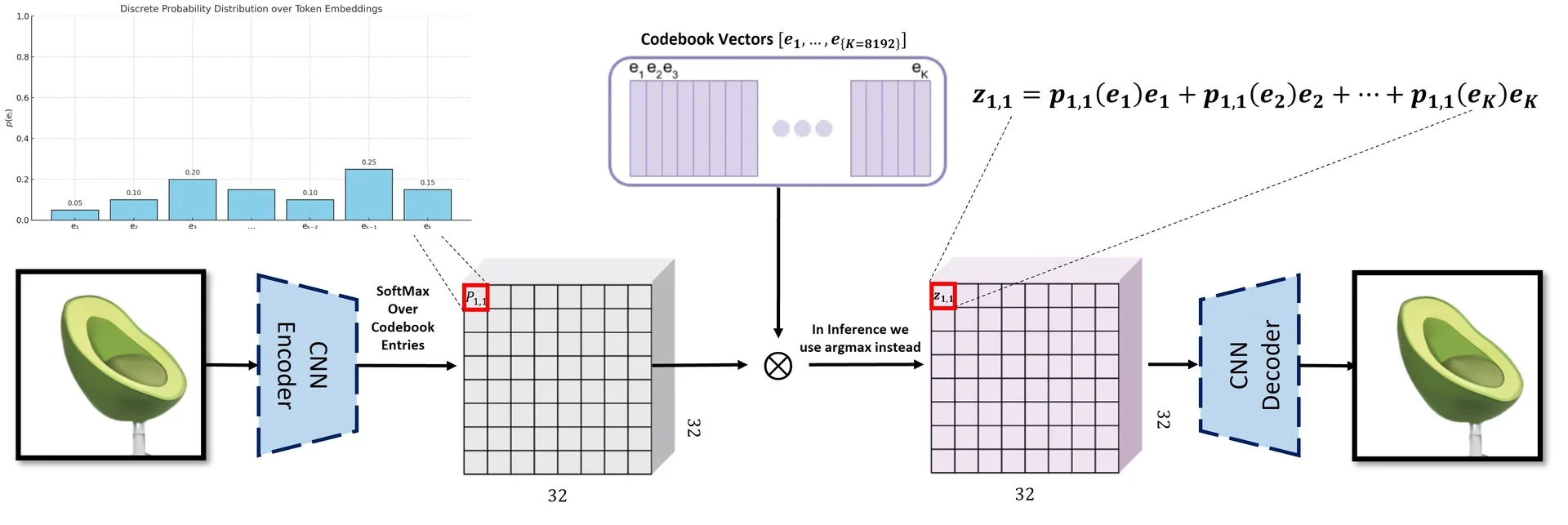
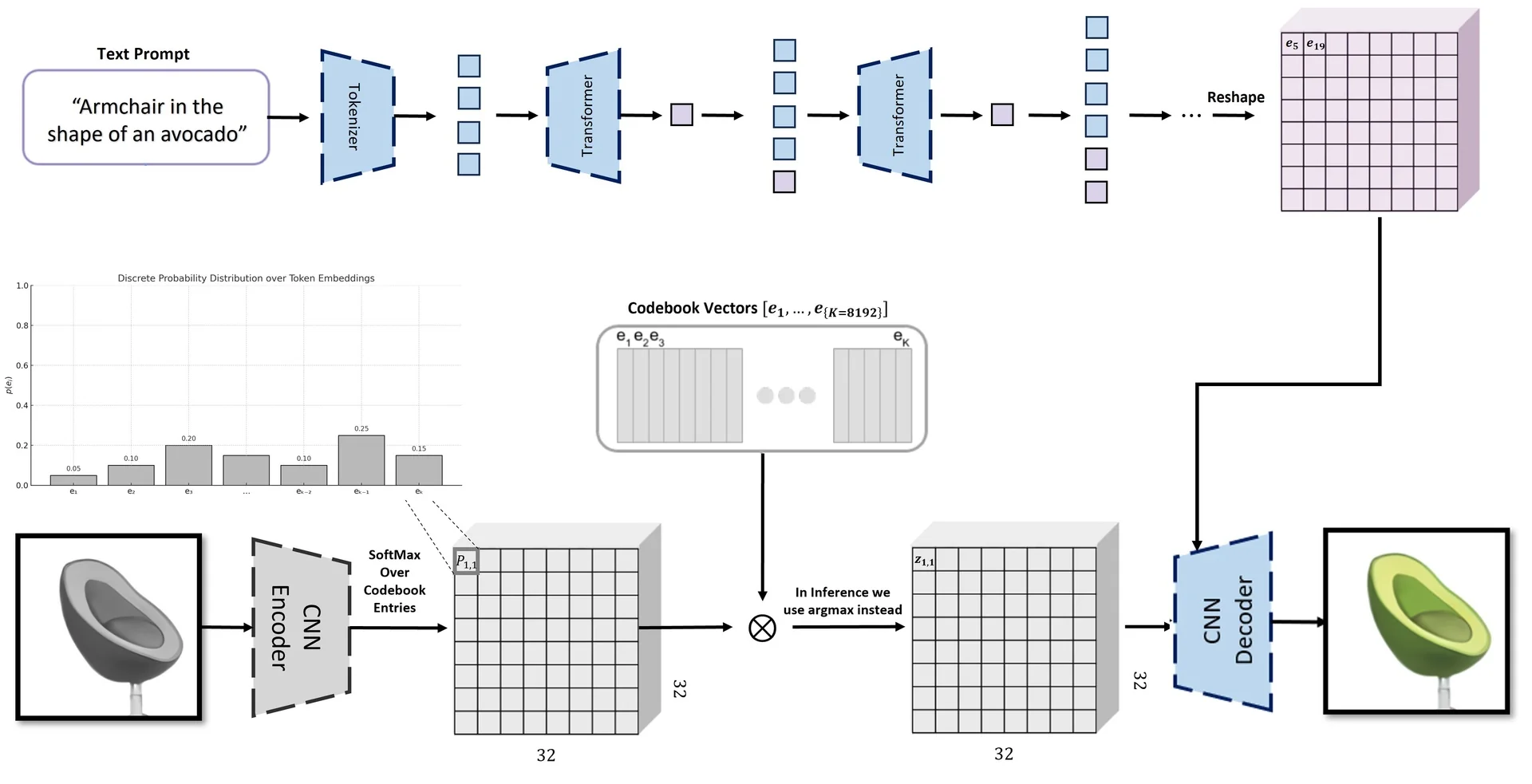
Rather than passing the encoder outputs directly to the decoder, each position in the latent maps is replaced by its closest vector from a learned codebook.
Intuition: Think of the codebook as a fixed “dictionary” of feature prototypes. Just as we approximate a sentence using a limited vocabulary of words, VQ-VAE approximates an image using a limited vocabulary of learnable feature vectors.
Each codebook is a set of \( K \) discrete embedding vectors: \[ \mathcal {C} = \{ \mathbf {e}_k \in \mathbb {R}^d \}_{k=1}^K \] Quantization proceeds by computing, for each latent vector \( \mathbf {z}_e(i, j) \), its nearest codebook entry: \[ \mathbf {z}_q(i,j) = \mathbf {e}_{k^\star }, \quad \mbox{where } k^\star = \operatorname *{argmin}_{k} \| \mathbf {z}_e(i,j) - \mathbf {e}_k \|_2 \]
This process converts the encoder output \( \mathbf {z}_e \in \mathbb {R}^{H_l \times W_l \times d} \) (for each level \( l \in \{b, t\} \)) into a quantized tensor \( \mathbf {z}_q \in \mathbb {R}^{H_l \times W_l \times d} \), and a corresponding index map: \[ \mathbf {i}_l \in \{1, \dots , K\}^{H_l \times W_l} \] The quantized representation consists of the code vectors \( \mathbf {z}_l^q(i,j) = \mathcal {C}^{(l)}[\mathbf {i}_l(i,j)] \).
Why this matters:
- It creates a discrete latent space with symbolic representations and structured reuse of learned patterns.
- Discretization acts as a form of regularization, preventing the encoder outputs from drifting.
- Why not use continuous embeddings? In continuous VAEs, the model often “cheats” by hiding microscopic details in the infinite precision of the latent vector. Discretization forces the model to keep only the essential feature prototypes.
- Most importantly, it enables the use of autoregressive priors (PixelCNN) that model the distribution over discrete indices. These models are exceptionally good at predicting discrete tokens (like words in a language model) but struggle to model complex continuous distributions.
-
Shared Decoder (Coarse-to-Fine Reconstruction):
The quantized latents from both levels are passed to a shared decoder:
- The top-level quantized embedding map \( \mathbf {z}_t^q \in \mathbb {R}^{H_t \times W_t \times d} \) is first decoded into a coarse semantic feature map.
- The bottom-level quantized embedding \( \mathbf {z}_b^q \in \mathbb {R}^{H_b \times W_b \times d} \) is then decoded conditioned on the top-level output.
This coarse-to-fine strategy improves reconstruction quality and allows the decoder to combine semantic context with fine detail.
-
Autoregressive Priors (Trained After Autoencoder):
Once the VQ-VAE-2 autoencoder (i.e., encoders, decoder, and codebooks) has been trained to reconstruct images, we introduce two PixelCNN-based autoregressive priors to enable data generation from scratch.
These models operate over the discrete index maps produced during quantization:
- \( \mbox{PixelCNN}_t \) models the unconditional prior \( p(\mathbf {i}_t) \), i.e., the joint distribution over top-level latent indices. It is trained autoregressively in raster scan order over the 2D grid \( H_t \times W_t \).
- \( \mbox{PixelCNN}_b \) models the conditional prior \( p(\mathbf {i}_b \mid \mathbf {i}_t) \), i.e., the distribution of bottom-level code indices given the sampled top-level indices. It is also autoregressive over the spatial positions \( H_b \times W_b \), but each prediction is conditioned on both previous bottom-level indices and the entire top-level map \( \mathbf {i}_t \).
Choice of Autoregressive Prior: PixelCNN vs. PixelRNN/LSTMs
While the VQ-VAE-2 architecture uses PixelCNN, other autoregressive sequence models exist. It is important to understand the trade-offs that motivate this choice:
- Recurrent Models (PixelRNN, Diagonal BiLSTM): RNN-based approaches, such as PixelRNN (which includes Row LSTM and Diagonal BiLSTM variants), are valid autoregressive models. Because they rely on recurrent hidden states, they theoretically have an infinite receptive field and can model complex long-range dependencies effectively.
- Why PixelCNN is preferred: Despite the theoretical power of LSTMs, they are inherently sequential—computing pixel \(t\) requires the hidden state from \(t-1\). This makes training slow and difficult to parallelize over large 2D grids. In contrast, PixelCNN uses masked convolutions. This allows the model to compute the probability of all indices in the map simultaneously during training (parallelization), offering a crucial speed and scalability advantage for the high-resolution hierarchical maps in VQ-VAE-2.
Note on Dimensions: The PixelCNN does not input the high-dimensional VQ vectors (e.g., size 64). It inputs the indices (integers). Internally, the PixelCNN learns its own separate, smaller embeddings optimized for sequence prediction.
How does autoregressive sampling begin? PixelCNN models generate a grid of indices one element at a time, using a predefined order (e.g., row-major order). To start the generation process:
- The first pixel (i.e., top-left index \( \mathbf {i}_t(1,1) \)) is sampled from a learned marginal distribution (or initialized with a zero-padding context).
- Subsequent pixels are sampled conditioned on all previously generated values (e.g., \( \mathbf {i}_t(1,2) \sim p(i_{1,2} \mid i_{1,1}) \), and so on).
This sampling continues until all elements of \( \mathbf {i}_t \) and \( \mathbf {i}_b \) are filled in.
How does this enable generation? Once we have sampled both latent index maps:
- 1.
- Retrieve the quantized embeddings \( \mathbf {z}_t^q = \mathcal {C}^{(t)}[\mathbf {i}_t] \) and \( \mathbf {z}_b^q = \mathcal {C}^{(b)}[\mathbf {i}_b] \).
- 2.
- Feed both into the trained decoder: \( \hat {\mathbf {x}} = \mbox{Decoder}(\mathbf {z}_t^q, \mathbf {z}_b^q) \).
This approach allows us to sample novel images with global coherence (via top-level modeling) and local realism (via bottom-level refinement), while reusing the learned latent structure of the VQ-VAE-2 encoder-decoder pipeline.
Summary Table: Dimensional Flow and Index Usage
| Stage | Tensor Shape | Description |
|---|---|---|
| Input Image \( \mathbf {x} \) | \( H \times W \times C \) | Original RGB (or grayscale) image given as input to the VQ-VAE-2 pipeline. |
| Bottom Encoder Output \( \mathbf {z}_b^e \) | \( H_b \times W_b \times d \) | Bottom-level continuous latent map produced by the first encoder. Captures fine-scale features. |
| Top Encoder Output \( \mathbf {z}_t^e \) | \( H_t \times W_t \times d \) | Top-level continuous latent map obtained by passing \( \mathbf {z}_b^e \) through the second encoder. Captures high-level, coarse information. |
| Top-Level Index Map \( \mathbf {i}_t \) | \( H_t \times W_t \) | At each spatial location \( (i,j) \), stores index of the nearest codebook vector in \( \mathcal {C}^{(t)} \) for \( \mathbf {z}_t^e(i,j) \). |
| Bottom-Level Index Map \( \mathbf {i}_b \) | \( H_b \times W_b \) | At each spatial location \( (i,j) \), stores index of the nearest codebook vector in \( \mathcal {C}^{(b)} \) for \( \mathbf {z}_b^e(i,j) \). |
| Quantized Top-Level \( \mathbf {z}_t^q \) | \( H_t \times W_t \times d \) | Latent tensor constructed by replacing each feature in \( \mathbf {z}_t^e \) with the corresponding codebook vector from \( \mathcal {C}^{(t)} \) using \( \mathbf {i}_t \). |
| Quantized Bottom-Level \( \mathbf {z}_b^q \) | \( H_b \times W_b \times d \) | Latent tensor constructed by replacing each feature in \( \mathbf {z}_b^e \) with the corresponding codebook vector from \( \mathcal {C}^{(b)} \) using \( \mathbf {i}_b \). |
| Reconstructed Image \( \hat {\mathbf {x}} \) | \( H \times W \times C \) | Final decoded image produced by feeding \( \mathbf {z}_t^q \) and \( \mathbf {z}_b^q \) into the decoder in a coarse-to-fine manner. |
Next: Training and Inference Flow Now that the architecture is defined, we proceed to describe the full training process. This includes:
- The VQ-VAE loss decomposition: reconstruction, codebook, and commitment losses.
- How gradients flow with the use of the stop-gradient operator.
- Post-hoc training of PixelCNNs over discrete index maps.
- Image generation during inference: sampling \( \mathbf {i}_t \rightarrow \mathbf {i}_b \rightarrow \hat {\mathbf {x}} \).
Training the VQ-VAE-2 Autoencoder
Objective Overview The VQ-VAE-2 model is trained to reconstruct input images while simultaneously learning a meaningful discrete latent space. Its objective function is composed of three terms:
\[ \mathcal {L}_{\mbox{VQ-VAE-2}} = \underbrace {\mathcal {L}_{\mbox{recon}}}_{\mbox{Image Fidelity}} + \underbrace {\mathcal {L}_{\mbox{codebook}}}_{\mbox{Codebook Update}} + \underbrace {\beta \cdot \mathcal {L}_{\mbox{commit}}}_{\mbox{Encoder Regularization}} \]
Each term serves a different purpose in enabling a stable and effective quantized autoencoder. We now explain each one.
1. Reconstruction Loss (\( \mathcal {L}_{\mbox{recon}} \)) This term encourages the decoder to faithfully reconstruct the input image from the quantized latent codes: \[ \mathcal {L}_{\mbox{recon}} = \| \mathbf {x} - \hat {\mathbf {x}} \|_2^2 \] Here, \( \hat {\mathbf {x}} = D(\mathbf {z}_t^q, \mathbf {z}_b^q) \) is the image reconstructed from the quantized top and bottom latent maps. This is a pixel-wise squared error (or optionally a negative log-likelihood if modeling pixels probabilistically).
Why is the reconstruction sometimes blurry? The use of \( L_2 \) loss (Mean Squared Error) mathematically forces the model to predict the mean (average) of all plausible pixel values.
- Example: If the model is unsure whether an edge should be black (0) or white (255), the “safest” prediction to minimize \( L_2 \) error is gray (127). This averaging creates blur.
- L1 vs L2: While \( L_1 \) loss forces the model to predict the median (which can be slightly sharper/less sensitive to outliers), it still fundamentally penalizes pixel-level differences rather than perceptual realism.
- Solution: To fix this, modern successors (like VQ-GAN) add an Adversarial Loss, which penalizes the model if the texture looks “fake” or blurry, regardless of the pixel math.
2. Codebook Update (\( \mathcal {L}_{\mbox{codebook}} \)) In VQ-VAE, the encoder produces a continuous latent vector at each spatial location, but the model then quantizes this vector to the nearest entry in a learned codebook. Let \[ \mathbf {z}_e(i,j) \in \mathbb {R}^d \quad \mbox{and}\quad \mathcal {C} = \{\mathbf {e}_k\}_{k=1}^{K},\ \mathbf {e}_k \in \mathbb {R}^d \] denote the encoder output and a codebook of \(K\) embeddings, respectively. Quantization selects a discrete index via a nearest-neighbor lookup: \[ k^\star (i,j) \;=\; \operatorname *{argmin}_{k \in \{1,\dots ,K\}} \left \| \mathbf {z}_e(i,j) - \mathbf {e}_k \right \|_2, \qquad \mathbf {z}_q(i,j) \;=\; \mathbf {e}_{k^\star (i,j)}. \]
Why non-differentiability matters. The mapping \(\mathbf {z}_e \mapsto k^\star \) involves an \(\operatorname *{argmin}\) over discrete indices, which is non-differentiable: infinitesimal changes in \(\mathbf {z}_e\) typically do not change the selected index \(k^\star \). Consequently, standard backpropagation cannot propagate gradients through the index selection to instruct the encoder on how to adjust \(\mathbf {z}_e\).
VQ-VAE resolves this by decoupling the updates:
- For the Encoder: It uses a straight-through gradient estimator, effectively copying gradients from the decoder input \(\mathbf {z}_q\) directly to the encoder output \(\mathbf {z}_e\) during the backward pass (treating quantization as an identity map for gradients).
- For the Codebook: It uses a separate update rule to explicitly move the embedding vectors \(\mathbf {e}_k\) toward the encoder outputs that selected them.
There are two standard strategies to implement this codebook update: a gradient-based objective (from the original VQ-VAE) and an EMA-based update (a commonly used stable alternative).
(a) Gradient-Based Codebook Loss (Original VQ-VAE) In this approach, the codebook embeddings are optimized by minimizing the squared distance between each selected embedding and the corresponding encoder output. Crucially, we stop gradients flowing into the encoder for this term so that it updates only the codebook: \begin {equation} \mathcal {L}_{\mbox{codebook}} = \left \| \texttt{sg}[\mathbf {z}_e(i,j)] - \mathbf {e}_{k^\star (i,j)} \right \|_2^2. \label {eq:chapter20_vqvae_codebook_loss} \end {equation}
Here \(\texttt{sg}[\cdot ]\) denotes the stop-gradient operator. This treats \(\mathbf {z}_e\) as a constant constant, ensuring that:
- \(\mathcal {L}_{\mbox{codebook}}\) pulls the code \(\mathbf {e}_{k^\star }\) toward the data point \(\mathbf {z}_e\) (a prototype update).
- The encoder is not pulled toward the codebook by this loss, preventing the two from ”chasing” each other unstably.
To prevents the encoder outputs from drifting arbitrarily far from the codebook, VQ-VAE requires a separate commitment loss that pulls the encoder toward the code: \begin {equation} \mathcal {L}_{\mbox{commit}} = \beta \left \| \mathbf {z}_e(i,j) - \texttt{sg}[\mathbf {e}_{k^\star (i,j)}] \right \|_2^2. \label {eq:chapter20_vqvae_commitment_loss} \end {equation} Intuitively, \(\mathcal {L}_{\mbox{codebook}}\) updates the codes to match the data, while \(\mathcal {L}_{\mbox{commit}}\) updates the encoder to commit to the chosen codes.
(b) EMA-Based Codebook Update (Used in Practice) An alternative strategy, widely used in modern implementations, updates the codebook using an Exponential Moving Average (EMA). To understand this approach, it is helpful to view Vector Quantization as an online version of K-Means clustering.
Intuition: The Centroid Logic. In ideal clustering, the optimal position for a cluster center (codebook vector \(\mathbf {e}_k\)) is the average (centroid) of all data points (encoder outputs \(\mathbf {z}_e\)) assigned to it. \[ \mathbf {e}_k^{\mbox{optimal}} = \frac {\sum \mathbf {z}_e \mbox{ assigned to } k}{\mbox{Count of } \mathbf {z}_e \mbox{ assigned to } k} \] Unlike K-Means, which processes the entire dataset at once, deep learning processes data in small batches. Updating the codebook to match the mean of a single batch would be unstable (the codebook would jump around wildly based on the specific images in that batch).
The EMA Solution. Instead of jumping to the batch mean, we maintain a running average of the sum and the count over time. We define two running statistics for each code \(k\):
- \(N_k\): The running count (total ”mass”) of encoder vectors assigned to code \(k\).
- \(M_k\): The running sum (total ”momentum”) of encoder vectors assigned to code \(k\).
For a given batch, we first compute the statistics just for that batch: \[ n_k^{\mbox{batch}} = \sum _{i,j} \mathbf {1}[k^\star (i,j)=k], \qquad m_k^{\mbox{batch}} = \sum _{i,j} \mathbf {1}[k^\star (i,j)=k] \,\mathbf {z}_e(i,j). \] We then smoothly update the long-term statistics using a decay factor \(\gamma \) (typically \(0.99\)): \begin {equation} N_k^{(t)} \leftarrow \underbrace {\gamma N_k^{(t-1)}}_{\mbox{History}} + \underbrace {(1-\gamma )\, n_k^{\mbox{batch}}}_{\mbox{New Data}}, \qquad M_k^{(t)} \leftarrow \gamma M_k^{(t-1)} + (1-\gamma )\, m_k^{\mbox{batch}}. \label {eq:chapter20_vqvae_ema_stats} \end {equation}
Deriving the Update. Finally, to find the current codebook vector \(\mathbf {e}_k\), we simply calculate the centroid using our running totals: \begin {equation} \mathbf {e}_k^{(t)} = \frac {\mbox{Total Sum}}{\mbox{Total Count}} = \frac {M_k^{(t)}}{N_k^{(t)}}. \label {eq:chapter20_vqvae_ema_codebook} \end {equation}
Why update this way?
- Stability: This method avoids the need for a learning rate on the codebook. The codebook vectors evolve smoothly as weighted averages of the data they represent, reducing the oscillatory behavior often seen with standard gradient descent.
- Robustness: It mimics running K-Means on the entire dataset stream, ensuring codes eventually converge to the true centers of the latent distribution.
In this variant, the encoder is still trained via the straight-through estimator and commitment loss. The only difference is that the codebook vectors are updated analytically, effectively smoothing out the prototype dynamics.
- Gradient-based: Updates \(\mathbf {e}_{k^\star }\) via \(\mathcal {L}_{\mbox{codebook}}\) (Eq. 20.7). Requires balancing with commitment loss; moves codes via standard optimizer steps.
- EMA-based: Updates \(\mathbf {e}_k\) via running statistics (Eq. 20.10). Acts as a stable, online K-Means update, ignoring gradients for the codebook itself.
3. Commitment Loss (\( \mathcal {L}_{\mbox{commit}} \)) This term encourages encoder outputs to stay close to the quantized embeddings to which they are assigned: \[ \mathcal {L}_{\mbox{commit}} = \| \mathbf {z}_e - \texttt{sg}[\mathbf {e}] \|_2^2 \] Here, we stop the gradient on \( \mathbf {e} \), updating only the encoder. This penalizes encoder drift and forces it to ”commit” to one of the fixed embedding vectors in the codebook.
Why Two Losses with Stop-Gradients Are Needed We require both the codebook and commitment losses to properly manage the interaction between the encoder and the discrete latent space.
Intuition: The Dog and the Mat. Why can’t we just let both the encoder and codebook update freely toward each other? Imagine trying to teach a dog (the Encoder) to sit on a mat (the Codebook Vector).
- Without Stop Gradients (The Chase): If you move the mat toward the dog at the same time the dog moves toward the mat, they will meet in a random middle spot. Next time, the dog moves further, and the mat chases it again. The mat never stays in one place long enough to become a reliable reference point (“anchor”). The codebook vectors would wander endlessly (oscillate) and fail to form meaningful clusters.
-
With Stop Gradients (Alternating Updates):
- Codebook Loss: We freeze the Encoder. We move the Codebook vector to the center of the data points assigned to it (like moving the mat to where the dog prefers to sit). This makes the codebook a good representative of the data.
- Commitment Loss: We freeze the Codebook. We force the Encoder to produce outputs close to the current Codebook vector. This prevents the Encoder’s output from growing arbitrarily large or drifting away from the allowed ”dictionary” of codes.
The stop-gradient operator ensures that only one component — either the encoder or the codebook — is updated by each loss term. This separation is essential for training stability.
Compact Notation for Vector Quantization Loss The two terms above are often grouped together as the vector quantization loss: \[ \mathcal {L}_{\mbox{VQ}} = \| \texttt{sg}[\mathbf {z}_e] - \mathbf {e} \|_2^2 + \beta \| \mathbf {z}_e - \texttt{sg}[\mathbf {e}] \|_2^2 \]
- 1.
- Encode the image \( \mathbf {x} \) into latent maps: \[ \mathbf {x} \rightarrow \mathbf {z}_b^e \rightarrow \mathbf {z}_t^e \]
- 2.
- Quantize both latent maps: \[ \mathbf {z}_b^q(i,j) = \mathcal {C}^{(b)}[\mathbf {i}_b(i,j)], \quad \mathbf {z}_t^q(i,j) = \mathcal {C}^{(t)}[\mathbf {i}_t(i,j)] \] where \( \mathbf {i}_b, \mathbf {i}_t \in \{1, \dots , K\} \) are index maps pointing to codebook entries.
- 3.
- Decode the quantized representations: \[ \hat {\mathbf {x}} = D(\mathbf {z}_t^q, \mathbf {z}_b^q) \]
- 4.
- Compute the total loss: \[ \mathcal {L} = \| \mathbf {x} - \hat {\mathbf {x}} \|_2^2 + \sum _{\ell \in \{t,b\}} \left [ \| \texttt{sg}[\mathbf {z}_e^{(\ell )}] - \mathbf {e}^{(\ell )} \|_2^2 + \beta \| \mathbf {z}_e^{(\ell )} - \texttt{sg}[\mathbf {e}^{(\ell )}] \|_2^2 \right ] \]
- 5.
- Backpropagate gradients and update:
- Encoder and decoder weights.
- Codebook embeddings.
Training Summary with EMA Codebook Updates If using EMA for codebook updates, the total loss becomes:
\[ \mathcal {L}_{\mbox{VQ-VAE-2}} = \underbrace {\| \mathbf {x} - \hat {\mathbf {x}} \|_2^2}_{\mbox{Reconstruction}} + \underbrace {\beta \| \mathbf {z}_e - \texttt{sg}[\mathbf {e}] \|_2^2}_{\mbox{Commitment Loss}} \]
The codebook is updated separately using exponential moving averages, not through gradient-based optimization.
This concludes the training of the VQ-VAE-2 autoencoder. Once trained and converged, the encoder, decoder, and codebooks are frozen, and we proceed to the next stage: training the autoregressive PixelCNN priors over the discrete latent indices.
Training the Autoregressive Priors
Motivation Once the VQ-VAE-2 autoencoder has been trained to compress and reconstruct images via quantized latents, we aim to turn it into a fully generative model. However, we cannot directly sample from the latent codebooks unless we learn to generate plausible sequences of discrete latent indices — this is where PixelCNN priors come into play.
These priors model the distribution over the discrete index maps produced by the quantization process: \[ \mathbf {i}_t \in \{1, \dots , K\}^{H_t \times W_t}, \quad \mathbf {i}_b \in \{1, \dots , K\}^{H_b \times W_b} \]
Hierarchical Modeling: Why separate priors? Two PixelCNNs are trained after the autoencoder components (encoders, decoder, codebooks) have been frozen. We use two separate models because they solve fundamentally different probability tasks:
-
Top-Level Prior (\( \mbox{PixelCNN}_t \)):
This models the unconditional prior \( p(\mathbf {i}_t) \), i.e., the joint distribution over top-level latent indices. It generates the “big picture” structure from scratch and has no context to rely on. \[ p(\mathbf {i}_t) = \prod _{h=1}^{H_t} \prod _{w=1}^{W_t} p\left ( \mathbf {i}_t[h, w] \,\middle |\, \mathbf {i}_t[<h, :],\, \mathbf {i}_t[h, <w] \right ) \] Here, each index is sampled conditioned on previously generated indices in raster scan order — rows first, then columns.
-
Bottom-Level Prior (\( \mbox{PixelCNN}_b \)):
This models the conditional prior \( p(\mathbf {i}_b \mid \mathbf {i}_t) \). It fills in fine details (texture). Crucially, it is conditioned on the top-level map. It asks: “Given that the top level says this area is a Face, what specific skin texture pixels should I put here?” \[ p(\mathbf {i}_b \mid \mathbf {i}_t) = \prod _{h=1}^{H_b} \prod _{w=1}^{W_b} p\left ( \mathbf {i}_b[h, w] \,\middle |\, \mathbf {i}_b[<h, :],\, \mathbf {i}_b[h, <w],\, \mathbf {i}_t \right ) \] Each index \( \mathbf {i}_b[h,w] \) is conditioned on both previously generated indices in \( \mathbf {i}_b \) and the full top-level map \( \mathbf {i}_t \).
- The PixelCNNs are trained using standard cross-entropy loss on the categorical distributions over indices.
- Training examples are collected by passing training images through the frozen encoder and recording the resulting index maps \( \mathbf {i}_t \), \( \mathbf {i}_b \).
-
The models are trained separately:
- PixelCNN\(_t\): trained on samples of \( \mathbf {i}_t \)
- PixelCNN\(_b\): trained on \( \mathbf {i}_b \) conditioned on \( \mathbf {i}_t \)
Sampling Procedure At inference time (for unconditional generation), we proceed as follows:
- 1.
- Sample \( \hat {\mathbf {i}}_t \sim p(\mathbf {i}_t) \) using PixelCNN\(_t\).
- 2.
- Sample \( \hat {\mathbf {i}}_b \sim p(\mathbf {i}_b \mid \hat {\mathbf {i}}_t) \) using PixelCNN\(_b\).
- 3.
- Retrieve quantized codebook vectors: \[ \mathbf {z}_t^q[h, w] = \mathcal {C}^{(t)}[\hat {\mathbf {i}}_t[h, w]], \quad \mathbf {z}_b^q[h, w] = \mathcal {C}^{(b)}[\hat {\mathbf {i}}_b[h, w]] \]
- 4.
- Decode \( (\mathbf {z}_t^q, \mathbf {z}_b^q) \rightarrow \hat {\mathbf {x}} \)
Initialization Note Since PixelCNNs are autoregressive models, they generate each element of the output one at a time, conditioned on the previously generated elements in a predefined order (usually raster scan — left to right, top to bottom). However, at the very beginning of sampling, no context exists yet for the first position.
To address this, we initialize the grid of latent indices with an empty or neutral state — typically done by either:
- Padding the grid with a fixed value (e.g., all zeros) to serve as an artificial context for the first few pixels.
- Treating the first position \( (0,0) \) as unconditional and sampling it directly from the learned marginal distribution.
From there, sampling proceeds autoregressively:
- For each spatial position \( (h, w) \), the PixelCNN uses all previously sampled values (e.g., those above and to the left of the current location) to predict a probability distribution over possible code indices.
- A discrete index is sampled from this distribution, placed at position \( (h, w) \), and used as context for the next position.
This procedure is repeated until the full latent index map is generated.
Advantages and Limitations of VQ-VAE-2 VQ-VAE-2 couples a discrete latent autoencoder with autoregressive priors (PixelCNN-style) over latent indices. This hybrid design inherits strengths from both latent-variable modeling and autoregressive likelihood modeling, but it also exposes specific trade-offs.
-
Advantages
- High-quality generation via abstract autoregression. Instead of predicting pixels one-by-one, the prior models the joint distribution of discrete latent indices at a much lower spatial resolution. This pushes autoregression to a more abstract level, capturing long-range global structure (layout, pose) while the decoder handles local detail.
- Efficient sampling relative to pixel-space. By operating on a compressed (and hierarchical) grid of latent indices, the effective sequence length is drastically reduced compared to full-resolution pixel autoregression, making high-resolution synthesis more practical.
- Modularity and reuse. The learned discrete autoencoder provides a standalone, reusable image decoder. One can retrain the computationally cheaper PixelCNN prior for new tasks (e.g., class-conditional generation) while keeping the expensive autoencoder fixed.
- Compact, semantically structured representation. Vector quantization yields a discrete code sequence that acts as a learned compression of the image, naturally suiting tasks like compression, retrieval, and semantic editing.
-
Limitations
- Sequential priors remain a bottleneck. Despite the compressed grid, the priors generate indices sequentially (raster-scan order). This inherent sequentiality limits inference speed compared to fully parallel (one-shot) generators.
- Training complexity. The multi-stage pipeline—(i) training the discrete autoencoder, then (ii) training hierarchical priors—is often more cumbersome to tune and engineer compared to end-to-end approaches.
- Reconstruction bias (Blur). The autoencoder is typically trained with pixel-space losses (like \(L_2\)), which mathematically favor ”average” predictions. This can result in a loss of high-frequency texture details, as the model avoids committing to sharp, specific modes in the output distribution.
The Pivot to Adversarial Learning. While VQ-VAE-2 achieved state-of-the-art likelihood results, the limitations highlighted above—specifically the sequential sampling speed and the blur induced by reconstruction losses—set the stage for our next topic.
To achieve real-time, one-shot generation and to optimize strictly for perceptual realism (ignoring pixel-wise averages), we must abandon explicit density estimation. We now turn to Generative Adversarial Networks (GANs), which solve these problems by training a generator not to match a probability distribution, but to defeat a competitor.
20.4 Generative Adversarial Networks (GANs)
Bridging from Autoregressive Models, VAEs to GANs Up to this point, we have studied explicit generative models:
- Autoregressive models (e.g., PixelCNN) directly model the data likelihood \( p(\mathbf {x}) \) by factorizing it into a sequence of conditional distributions. These models produce high-quality samples but suffer from slow sampling, since each pixel (or token) is generated sequentially.
- Variational Autoencoders (VAEs) introduce latent variables \( \mathbf {z} \) and define a variational lower bound on \( \log p(\mathbf {x}) \), which they optimize during training. While VAEs allow fast sampling, their outputs are often blurry due to overly simplistic priors and decoders.
- VQ-VAE-2 combines the strengths of both worlds. It learns a discrete latent space via vector quantization, and models its distribution using autoregressive priors like PixelCNN — allowing for efficient compression and high-quality generation. Crucially, although it uses autoregressive models, sampling happens in a much lower-resolution latent space, making generation significantly faster than pixel-level autoregression.
Despite these advancements, all of the above methods explicitly define or approximate a probability density \( p(\mathbf {x}) \), or a lower bound thereof. This requires likelihood-based objectives and careful modeling of distributions, which can introduce challenges such as:
- Trade-offs between sample fidelity and likelihood maximization (e.g., in VAEs).
- Architectural constraints imposed by factorized likelihood models (e.g., PixelCNN).
This leads us to a fundamentally different approach: Generative Adversarial Networks (GANs). GANs completely sidestep the need to model \( p(\mathbf {x}) \) explicitly — instead, they define a sampling process that generates data, and train it using a learned adversary that distinguishes real from fake. In the next section, we introduce this adversarial framework in detail.
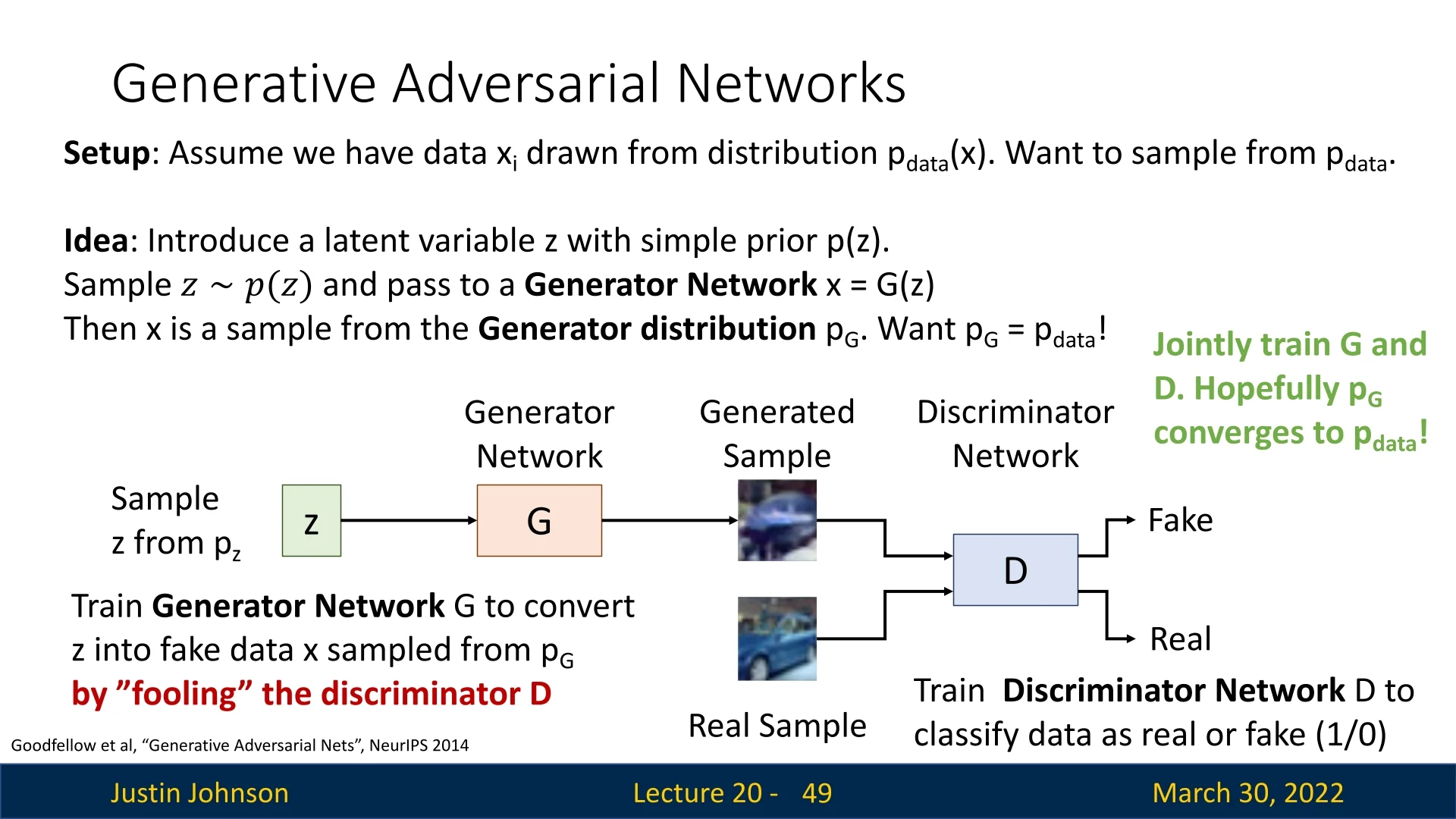
Enter GANs Generative Adversarial Networks (GANs) [180] are based on a radically different principle. Rather than trying to compute or approximate the density function \( p(\mathbf {x}) \), GANs focus on generating samples that are indistinguishable from real data.
They introduce a new type of generative model called an implicit model: we never write down \( p(\mathbf {x}) \), but instead learn a mechanism for sampling from it.
20.4.1 Setup: Implicit Generation via Adversarial Learning
Sampling from the True Distribution Let \( \mathbf {x} \sim p_{\mbox{data}}(\mathbf {x}) \) be a sample from the real data distribution — for instance, natural images. This distribution is unknown and intractable to express, but we assume we have access to i.i.d. samples from it (e.g., a dataset of images).
Our goal is to train a model whose samples are indistinguishable from those of \( p_{\mbox{data}} \). To this end, we adopt a latent variable model:
- Define a simple latent distribution \( p(\mathbf {z}) \), such as a standard Gaussian \( \mathcal {N}(0, \mathbf {I}) \) or uniform distribution.
- Sample a latent code \( \mathbf {z} \sim p(\mathbf {z}) \).
- Pass it through a neural network generator \( \mathbf {x} = G(\mathbf {z}) \) to produce a data sample.
This defines a generator distribution \( p_G(\mathbf {x}) \), where the sampling path is: \[ \mathbf {z} \sim p(\mathbf {z}) \quad \Rightarrow \quad \mathbf {x} = G(\mathbf {z}) \sim p_G(\mathbf {x}) \]
The key challenge is that we cannot write down \( p_G(\mathbf {x}) \) explicitly — it is an implicit distribution defined by the transformation of noise through a neural network.
Discriminator as a Learned Judge To bring \( p_G \) closer to \( p_{\mbox{data}} \), GANs introduce a second neural network: the discriminator \( D(\mathbf {x}) \), which is trained as a binary classifier. It receives samples from either the real distribution \( p_{\mbox{data}} \) or the generator \( p_G \), and must learn to classify them as: \[ D(\mathbf {x}) = \begin {cases} 1 & \mbox{if } \mathbf {x} \sim p_{\mbox{data}} \ (\mbox{real}) \\ 0 & \mbox{if } \mathbf {x} \sim p_G \ (\mbox{fake}) \end {cases} \]
The generator \( G \), meanwhile, is trained to fool the discriminator — it learns to produce samples that the discriminator cannot distinguish from real data.
Adversarial Training Dynamics The result is a two-player game: the generator tries to minimize the discriminator’s ability to detect fakes, while the discriminator tries to maximize its classification accuracy.
- The discriminator \( D \) is trained to maximize the probability of correctly identifying real vs. generated data.
- The generator \( G \) is trained to minimize this probability — i.e., to make generated data look real.
At equilibrium, the discriminator is maximally uncertain (i.e., it assigns probability 0.5 to all inputs), and the generator’s distribution \( p_G \) matches the real distribution \( p_{\mbox{data}} \).
Core Intuition The fundamental idea of GANs is to reframe generative modeling as a discrimination problem: if we can’t explicitly define what makes a good image, we can still train a network to tell real from fake — and then invert this process to generate better samples.
In the next part, we will formalize this game-theoretic setup and introduce the original GAN loss proposed by Goodfellow et al. [180], including its connection to Jensen–Shannon divergence, optimization challenges, and variants.
20.4.2 GAN Training Objective
We define a two-player minimax game between \( G \) and \( D \). The discriminator aims to classify real vs. fake images, while the generator tries to fool the discriminator. The objective function is: \[ \min _G \max _D \; V(D, G) = \mathbb {E}_{\mathbf {x} \sim p_{\mbox{data}}} \left [ \log D(\mathbf {x}) \right ] + \mathbb {E}_{\mathbf {z} \sim p(\mathbf {z})} \left [ \log (1 - D(G(\mathbf {z}))) \right ] \]
-
The discriminator maximizes both terms:
- \( \log D(\mathbf {x}) \) encourages \( D \) to classify real data as real (i.e., \( D(\mathbf {x}) \rightarrow 1 \)).
- \( \log (1 - D(G(\mathbf {z}))) \) encourages \( D \) to classify generated samples as fake (i.e., \( D(G(\mathbf {z})) \rightarrow 0 \)).
- The generator minimizes the second term: \[ \mathbb {E}_{\mathbf {z} \sim p(\mathbf {z})} \left [ \log (1 - D(G(\mathbf {z}))) \right ] \] This term is minimized when \( D(G(\mathbf {z})) \rightarrow 1 \), i.e., when the discriminator believes generated samples are real.
The generator and discriminator are trained jointly using alternating gradient updates: \[ \mbox{for } t = 1, \dots , T: \begin {cases} D \leftarrow D + \alpha _D \nabla _D V(G, D) \\ G \leftarrow G - \alpha _G \nabla _G V(G, D) \end {cases} \]
Difficulties in Optimization GAN training is notoriously unstable due to the adversarial dynamics. Two critical issues arise:
- No single loss is minimized: GAN training is a minimax game. The generator and discriminator influence each other’s gradients, making it difficult to assess convergence or use standard training curves.
-
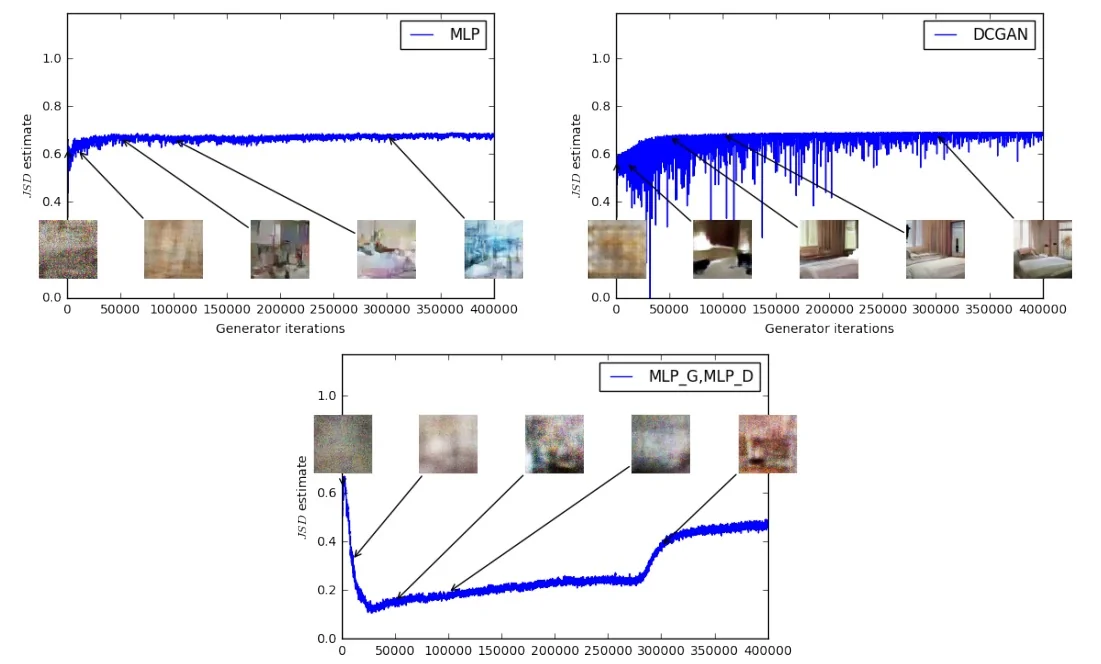
Vanishing gradients early in training: When \( G \) is untrained, it produces unrealistic images. This makes it easy for \( D \) to assign \( D(G(\mathbf {z})) \approx 0 \), saturating the term \( \log (1 - D(G(\mathbf {z}))) \). Since \( \log (1 - x) \) flattens near \( x = 0 \), this leads to vanishing gradients for the generator early on.
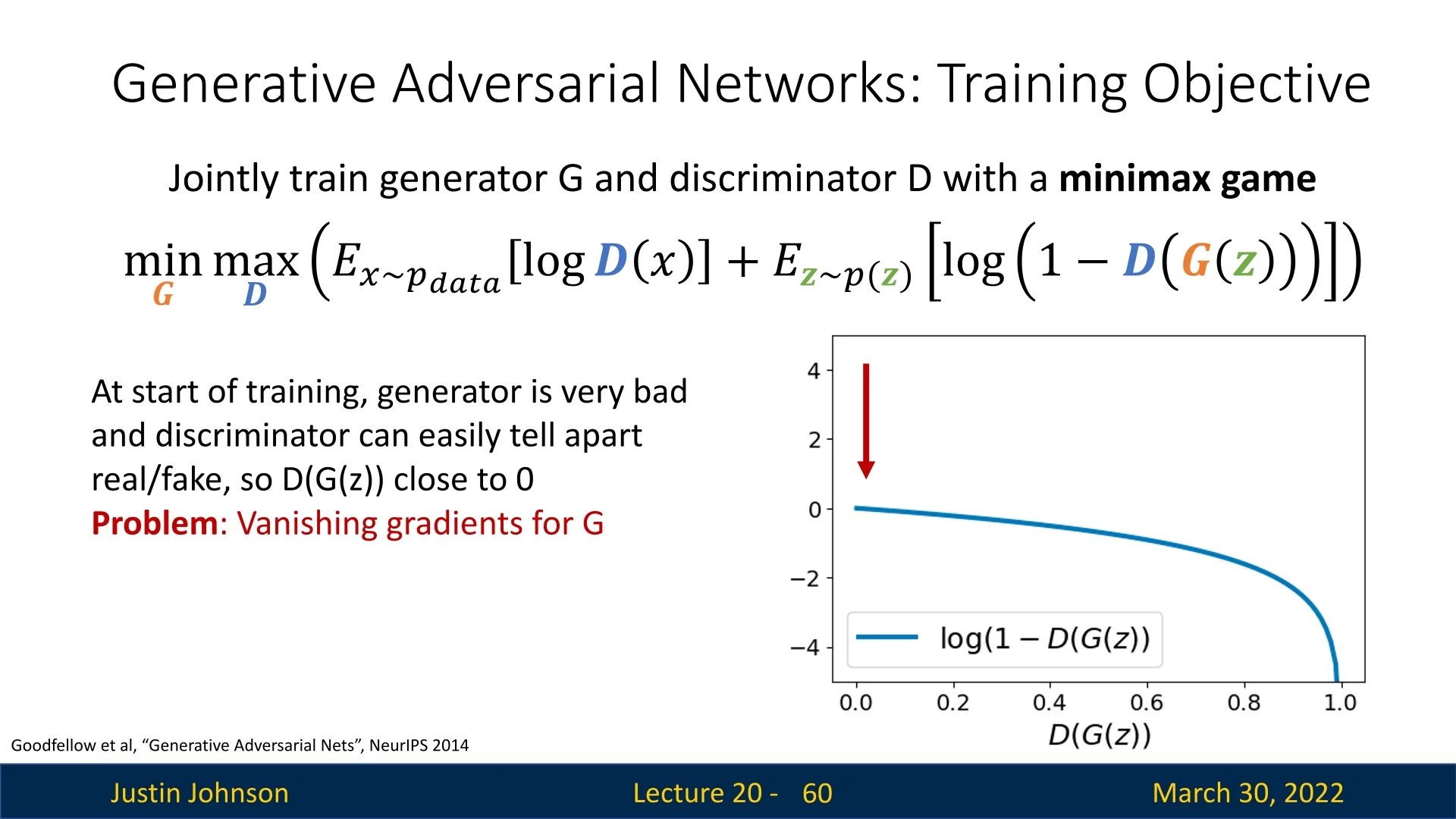
Figure 20.15: At the start of training, the generator produces poor samples. The discriminator easily identifies them, yielding vanishing gradients for the generator.
Modified Generator Loss (Non-Saturating Trick) In the original minimax objective proposed in [180], the generator is trained to minimize: \[ \mathbb {E}_{\mathbf {z} \sim p(\mathbf {z})} \left [ \log (1 - D(G(\mathbf {z}))) \right ] \] This objective encourages \( G \) to generate images that the discriminator believes are real. However, it suffers from a critical problem early in training: when the generator is poor and produces unrealistic images, the discriminator assigns very low scores \( D(G(\mathbf {z})) \approx 0 \). As a result, \( \log (1 - D(G(\mathbf {z}))) \approx 0 \), and its gradient vanishes: \[ \frac {\mathrm {d}}{\mathrm {d}G} \log (1 - D(G(\mathbf {z}))) \rightarrow 0 \]
This leads to extremely weak updates to the generator — just when it needs them most.
Solution: Switch the Objective Instead of minimizing \( \log (1 - D(G(\mathbf {z}))) \), we train the generator to maximize: \[ \mathbb {E}_{\mathbf {z} \sim p(\mathbf {z})} \left [ \log D(G(\mathbf {z})) \right ] \]
This change does not alter the goal — the generator still wants the discriminator to classify its outputs as real — but it yields stronger gradients, especially when \( D(G(\mathbf {z})) \) is small (i.e., when the discriminator is confident the generated image is fake).
Why does this work?
- For small inputs, \( \log (1 - x) \) is nearly flat (leading to vanishing gradients), while \( \log (x) \) is sharply sloped.
- So when \( D(G(\mathbf {z})) \) is close to zero, minimizing \( \log (1 - D(G(\mathbf {z}))) \) gives negligible gradients, while maximizing \( \log (D(G(\mathbf {z}))) \) gives large, informative gradients.
This variant is known as the non-saturating generator loss, and is widely used in practice for training stability.
Looking Ahead: Why This Objective? We have introduced the practical GAN training objective. But why this specific formulation? Is it theoretically sound? What happens when \( D \) is optimal? Does the generator recover the true data distribution \( p_{\mbox{data}} \)? In the next section, we analyze these questions and uncover the theoretical justification for adversarial training.
20.4.3 Why the GAN Training Objective Is Optimal
Step-by-Step Derivation We begin with the original minimax GAN objective from [180]. Our goal is to analyze the equilibrium of this game by characterizing the global minimum of the value function.
\begin {align*} \min _{\textcolor {darkorange}{G}} \max _{\textcolor {lightblue}{D}} \; & \mathbb {E}_{x \sim p_{\text {data}}}[\log \textcolor {lightblue}{D}(x)] + \mathbb {E}_{\textcolor {lightgreen}{z} \sim p(\textcolor {lightgreen}{z})}[\log (1 - \textcolor {lightblue}{D}(\textcolor {darkorange}{G}(\textcolor {lightgreen}{z})))] \quad \text {(Initial GAN objective)} \\ = \min _{\textcolor {darkorange}{G}} \max _{\textcolor {lightblue}{D}} \; & \mathbb {E}_{x \sim p_{\text {data}}}[\log \textcolor {lightblue}{D}(x)] + \mathbb {E}_{x \sim p_{\textcolor {darkorange}{G}}}[\log (1 - \textcolor {lightblue}{D}(x))] \quad \text {(Change of variables / LOTUS)} \\ = \min _{\textcolor {darkorange}{G}} \max _{\textcolor {lightblue}{D}} \; & \int _{\mathcal {X}} \left ( p_{\text {data}}(x) \log \textcolor {lightblue}{D}(x) + p_{\textcolor {darkorange}{G}}(x) \log (1 - \textcolor {lightblue}{D}(x)) \right ) dx \quad \text {(Definition of expectation)} \\ = \min _{\textcolor {darkorange}{G}} \; & \int _{\mathcal {X}} \max _{\textcolor {lightblue}{D(x)}} \left ( p_{\text {data}}(x) \log \textcolor {lightblue}{D}(x) + p_{\textcolor {darkorange}{G}}(x) \log (1 - \textcolor {lightblue}{D}(x)) \right ) dx \quad \text {(Push $\max _{\textcolor {lightblue}{D}}$ inside integral)} \end {align*}
Justification of the Mathematical Transformations To rigorously justify the steps above, we appeal to measure theory and the calculus of variations.
-
Change of Variables (The Pushforward and LOTUS):
The second term in the original objective is expressed as an expectation over latent variables \( \textcolor {lightgreen}{z} \sim p(\textcolor {lightgreen}{z}) \), with samples transformed through the generator: \( x = \textcolor {darkorange}{G}(\textcolor {lightgreen}{z}) \). This defines a new distribution over images, denoted \( \textcolor {darkorange}{p_G}(x) \), formally known as the pushforward measure (or generator distribution).The transition from an expectation over \( \textcolor {lightgreen}{z} \) to one over \( x \) is a direct application of the Law of the Unconscious Statistician (LOTUS). It guarantees that: \[ \mathbb {E}_{\textcolor {lightgreen}{z} \sim p(\textcolor {lightgreen}{z})} \left [ \log \left (1 - \textcolor {lightblue}{D}(\textcolor {darkorange}{G}(\textcolor {lightgreen}{z})) \right ) \right ] \quad \Rightarrow \quad \mathbb {E}_{x \sim \textcolor {darkorange}{p_G}(x)} \left [ \log \left (1 - \textcolor {lightblue}{D}(x) \right ) \right ] \] This reparameterization is valid because the pushforward distribution \( p_G \) exists. For the integral notation used subsequently, we further assume \( p_G \) admits a density with respect to the Lebesgue measure.
- Expectation to Integral:
Any expectation over a continuous random variable can be written as an integral: \[ \mathbb {E}_{x \sim p(x)}[f(x)] = \int _{\mathcal {X}} p(x) f(x) \, dx \] This applies to both the real data term and the generator term, allowing us to combine them into a single integral over the domain \( \mathcal {X} \). -
Pushing \( \max _D \) into the Integral (Functional Separability):
The discriminator \( \textcolor {lightblue}{D} \) is treated here as an arbitrary function defined pointwise over the domain \( \mathcal {X} \). This is an assumption of non-parametric optimization (i.e., we assume \( D \) has infinite capacity and is not constrained by a neural network architecture).Crucially, there is no dependence or coupling between \( \textcolor {lightblue}{D}(x_1) \) and \( \textcolor {lightblue}{D}(x_2) \) for different values of \( x \). Therefore, the objective functional is separable, and maximizing the global integral is equivalent to maximizing the integrand independently for each \( x \). \[ \max _{\textcolor {lightblue}{D}} \int _{\mathcal {X}} \cdots \; dx \quad \Longrightarrow \quad \int _{\mathcal {X}} \max _{\textcolor {lightblue}{D}(x)} \cdots \; dx \]
Solving the Inner Maximization (Discriminator) We now optimize the integrand pointwise for each \( x \in \mathcal {X} \), treating the discriminator output \( \textcolor {purple}{y} = \textcolor {purple}{D(x)} \) as a scalar variable. Define the objective at each point as: \[ f(\textcolor {purple}{y}) = \textcolor {darkred}{a} \log \textcolor {purple}{y} + \textcolor {darkeryellow}{b} \log (1 - \textcolor {purple}{y}), \quad \mbox{with} \quad \textcolor {darkred}{a} = p_{\mbox{data}}(x), \; \textcolor {darkeryellow}{b} = p_G(x) \] This function is strictly concave on \( \textcolor {purple}{y} \in (0, 1) \), and we compute the maximum by solving \( f'(\textcolor {purple}{y}) = 0 \): \[ f'(\textcolor {purple}{y}) = \frac {\textcolor {darkred}{a}}{\textcolor {purple}{y}} - \frac {\textcolor {darkeryellow}{b}}{1 - \textcolor {purple}{y}} = 0 \quad \Rightarrow \quad \textcolor {purple}{y} = \frac {\textcolor {darkred}{a}}{\textcolor {darkred}{a} + \textcolor {darkeryellow}{b}} \] Substituting back, the optimal value for the discriminator is: \[ \textcolor {lightblue}{D}^{*}_{\textcolor {darkorange}{G}}(x) = \frac {\textcolor {darkred}{p_{\mbox{data}}(x)}}{\textcolor {darkred}{p_{\mbox{data}}(x)} + \textcolor {darkeryellow}{p_G(x)}} \]
Here’s how the components map:
- \( p_{\mbox{data}}(x) \) (red) is the true data distribution at \( x \).
- \( D(x) \) (purple) is the scalar output of the discriminator.
- \( p_G(x) \) (dark yellow) is the generator’s distribution at \( x \).
This solution gives us the discriminator’s best possible output for any fixed generator \( G \). In the next step, we will plug this optimal discriminator back into the GAN objective to simplify the expression and reveal its connection to divergence measures.
Plugging the Optimal Discriminator into the Objective Having found the optimal discriminator \( \textcolor {lightblue}{D}^*_{\textcolor {darkorange}{G}} \) for a fixed generator, we now substitute it back into the game to evaluate the generator’s performance.
Recall that our goal is to minimize the value function \( V(\textcolor {darkorange}{G}, \textcolor {lightblue}{D}) \). Since the inner maximization is now solved, we focus on the Generator Value Function \( C(\textcolor {darkorange}{G}) \), which represents the generator’s loss when facing a perfect adversary: \[ C(\textcolor {darkorange}{G}) = \max _{\textcolor {lightblue}{D}} V(\textcolor {darkorange}{G}, \textcolor {lightblue}{D}) = V(\textcolor {darkorange}{G}, \textcolor {lightblue}{D}^*_{\textcolor {darkorange}{G}}) \]
To perform the substitution, let us first simplify the terms involving the optimal discriminator. Given \( \textcolor {lightblue}{D}^*_{\textcolor {darkorange}{G}}(x) = \frac {\textcolor {darkred}{p_{\mbox{data}}(x)}}{\textcolor {darkred}{p_{\mbox{data}}(x)} + \textcolor {darkeryellow}{p_G(x)}} \), the complementary probability (probability that the discriminator thinks a fake sample is fake) is: \[ 1 - \textcolor {lightblue}{D}^*_{\textcolor {darkorange}{G}}(x) = 1 - \frac {\textcolor {darkred}{p_{\mbox{data}}(x)}}{\textcolor {darkred}{p_{\mbox{data}}(x)} + \textcolor {darkeryellow}{p_G(x)}} = \frac {\textcolor {darkeryellow}{p_G(x)}}{\textcolor {darkred}{p_{\mbox{data}}(x)} + \textcolor {darkeryellow}{p_G(x)}} \]
We now replace \( \textcolor {lightblue}{D}(x) \) and \( (1-\textcolor {lightblue}{D}(x)) \) in the original integral objective with these expressions: \begin {align*} \min _{\textcolor {darkorange}{G}} C(\textcolor {darkorange}{G}) & = \min _{\textcolor {darkorange}{G}} \int _{\mathcal {X}} \Bigg ( \underbrace {\textcolor {darkred}{p_{\text {data}}(x)} \log \left ( \frac {\textcolor {darkred}{p_{\text {data}}(x)}} {\textcolor {darkred}{p_{\text {data}}(x)} + \textcolor {darkeryellow}{p_G(x)}} \right )}_{\text {Expected log-prob of real data}} + \underbrace {\textcolor {darkeryellow}{p_G(x)} \log \left ( \frac {\textcolor {darkeryellow}{p_G(x)}} {\textcolor {darkred}{p_{\text {data}}(x)} + \textcolor {darkeryellow}{p_G(x)}} \right )}_{\text {Expected log-prob of generated data}} \Bigg ) dx \end {align*}
Rewriting as KL Divergences The expression above resembles Kullback–Leibler (KL) divergence, but the denominators are sums, not distributions. To fix this, we need to compare \( \textcolor {darkred}{p_{\mbox{data}}} \) and \( \textcolor {darkeryellow}{p_G} \) against their average distribution (or mixture): \[ m(x) = \frac {\textcolor {darkred}{p_{\mbox{data}}(x)} + \textcolor {darkeryellow}{p_G(x)}}{2} \] We manipulate the log arguments by multiplying numerator and denominator by \( 2 \). This ”trick” is mathematically neutral (multiplying by \( 1 \)) but structurally revealing:
\begin {align*} = \min _{\textcolor {darkorange}{G}} \Bigg ( & \int _{\mathcal {X}} \textcolor {darkred}{p_{\text {data}}(x)} \log \left ( \frac {1}{2} \cdot \frac {\textcolor {darkred}{p_{\text {data}}(x)}}{\frac {\textcolor {darkred}{p_{\text {data}}(x)} + \textcolor {darkeryellow}{p_G(x)}}{2}} \right ) dx \\ + & \int _{\mathcal {X}} \textcolor {darkeryellow}{p_G(x)} \log \left ( \frac {1}{2} \cdot \frac {\textcolor {darkeryellow}{p_G(x)}}{\frac {\textcolor {darkred}{p_{\text {data}}(x)} + \textcolor {darkeryellow}{p_G(x)}}{2}} \right ) dx \Bigg ) \end {align*}
Using the logarithmic identity \( \log (a \cdot b) = \log a + \log b \), we separate the fraction \( \frac {1}{2} \) from the ratio of distributions. Note that \( \log (1/2) = -\log 2 \):
\begin {align*} = \min _{\textcolor {darkorange}{G}} \Bigg ( & \int _{\mathcal {X}} \textcolor {darkred}{p_{\text {data}}(x)} \left [ \log \left ( \frac {\textcolor {darkred}{p_{\text {data}}(x)}}{m(x)} \right ) - \log 2 \right ] dx \\ + & \int _{\mathcal {X}} \textcolor {darkeryellow}{p_G(x)} \left [ \log \left ( \frac {\textcolor {darkeryellow}{p_G(x)}}{m(x)} \right ) - \log 2 \right ] dx \Bigg ) \end {align*}
We now distribute the integrals. Since \( \textcolor {darkred}{p_{\mbox{data}}} \) and \( \textcolor {darkeryellow}{p_G} \) are valid probability distributions, they integrate to 1. Therefore, the constant terms \( -\log 2 \) sum to \( -2\log 2 = -\log 4 \). The remaining integrals are, by definition, KL divergences:
\begin {align*} = \min _{\textcolor {darkorange}{G}} \Bigg ( KL\left ( \textcolor {darkred}{p_{\text {data}}} \Big \| \frac {\textcolor {darkred}{p_{\text {data}}} + \textcolor {darkeryellow}{p_G}}{2} \right ) + KL\left ( \textcolor {darkeryellow}{p_G} \Big \| \frac {\textcolor {darkred}{p_{\text {data}}} + \textcolor {darkeryellow}{p_G}}{2} \right ) - \log 4 \Bigg ) \end {align*}
Introducing the Jensen–Shannon Divergence (JSD) The expression inside the minimization is related to the Jensen–Shannon Divergence (JSD), which measures the similarity between two probability distributions. Unlike KL divergence, JSD is symmetric and bounded. It is defined as: \[ JSD(p, q) = \frac {1}{2} KL\left ( p \Big \| \frac {p + q}{2} \right ) + \frac {1}{2} KL\left ( q \Big \| \frac {p + q}{2} \right ) \]
Final Result: Objective Minimizes JSD Substituting the JSD definition into our derived expression, the GAN training objective reduces to: \begin {align*} \min _{\textcolor {darkorange}{G}} C(\textcolor {darkorange}{G}) = \min _{\textcolor {darkorange}{G}} \left ( 2 \cdot JSD\left ( \textcolor {darkred}{p_{\text {data}}}, \textcolor {darkeryellow}{p_G} \right ) - {\log 4} \right ) \end {align*}
Interpretation:
- 1.
- The term \( -\log 4 \) represents the value of the game when the generator is perfect (confusion). Since \( \log 4 = 2 \log 2 \), this corresponds to the discriminator outputting \( 0.5 \) (uncertainty) for both real and fake samples: \( \log (0.5) + \log (0.5) = -\log 4 \).
- 2.
- Since \( JSD(p, q) \geq 0 \) with equality if and only if \( p = q \), the global minimum is achieved exactly when: \[ \textcolor {darkeryellow}{p_G(x)} = \textcolor {darkred}{p_{\mbox{data}}(x)} \]
This completes the proof: under idealized conditions (infinite capacity discriminator), the minimax game forces the generator to perfectly recover the data distribution.
Summary \begin {align*} \text {Optimal discriminator:} \quad &\textcolor {lightblue}{D}^{*}_{\textcolor {darkorange}{G}}(x) = \frac {\textcolor {darkred}{p_{\text {data}}(x)}}{\textcolor {darkred}{p_{\text {data}}(x)} + \textcolor {darkeryellow}{p_G(x)}} \\ \text {Global minimum:} \quad &\textcolor {purple}{p_G(x)} = \textcolor {darkred}{p_{\text {data}}(x)} \end {align*}
Important Caveats and Limitations of the Theoretical Result The optimality result derived above provides a crucial theoretical anchor: it guarantees that the minimax objective is statistically meaningful, identifying the data distribution as the unique global optimum. However, bridging the gap between this idealized theory and practical deep learning requires navigating several critical limitations.
-
Idealized Functional Optimization vs. Parameterized Networks. The derivation treats the discriminator \( D \) (and implicitly the generator \( G \)) as ranging over the space of all measurable functions. This ”non-parametric” or ”infinite capacity” assumption is what allows us to solve the inner maximization problem \(\max _D V(G,D)\) pointwise for every \( x \), yielding the closed-form \( D_G^* \).
In practice, we optimize over restricted families of functions parameterized by neural network weights, \( D_\phi \) and \( G_\theta \). The shared weights in a network introduce coupling between outputs—changing parameters to update \( D(x_1) \) inevitably affects \( D(x_2) \). Consequently: (i) The network family may not be expressive enough to represent the sharp, pointwise optimal discriminator \( D_G^* \); and (ii) Even if representable, the non-convex optimization landscape of the parameters may prevent gradient descent from finding it. Thus, the theorem proves that the game has the correct solution, not that a specific architecture trained with SGD will necessarily reach it.
-
The “Manifold Problem” and Vanishing Gradients. The JSD interpretation relies on the assumption that \( p_{\mbox{data}} \) and \( p_G \) have overlapping support with well-defined densities. In high-dimensional image spaces, however, distributions often concentrate on low-dimensional manifolds (e.g., the set of valid face images is a tiny fraction of the space of all possible pixel combinations).
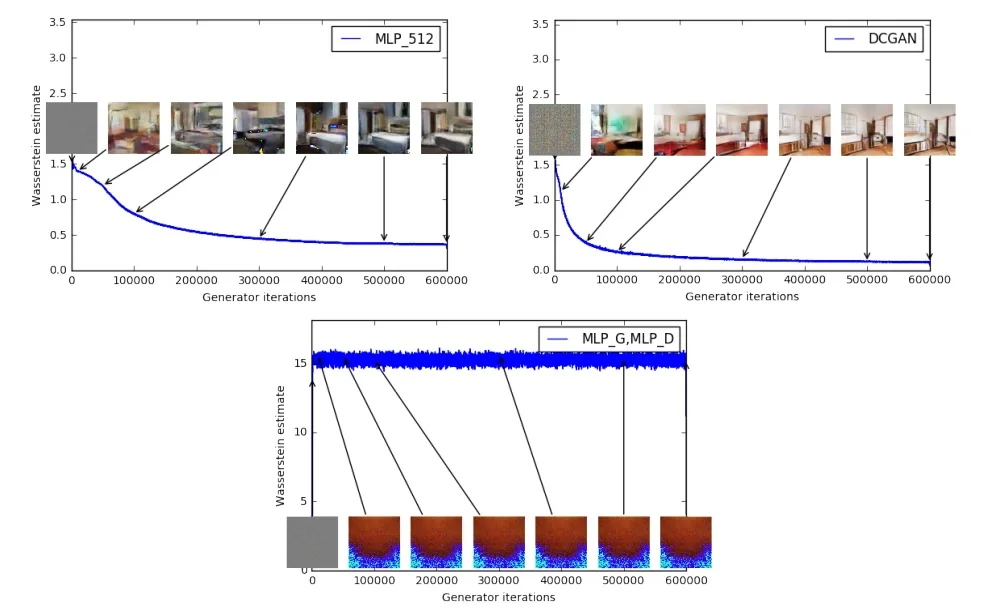
Early in training, these real and generated manifolds are likely to be disjoint. In this regime, a sufficiently capable discriminator can separate the distributions perfectly, setting \( D(x) \approx 1 \) on real data and \( D(x) \approx 0 \) on fake data. Mathematically, this causes the Jensen–Shannon divergence to saturate at its maximum value (constant \(\log 2\)). Since the gradient of a constant is zero, the generator receives no informative learning signal to guide it toward the data manifold. This geometry is the primary cause of the vanishing gradient problem in the original GAN formulation and motivates alternative objectives (like the non-saturating heuristic or Wasserstein distance) designed to provide smooth gradients even when distributions do not overlap.
-
Existence vs. Convergence (Statics vs. Dynamics). The proof characterizes the static equilibrium of the game: if we reach a state where \( p_G = p_{\mbox{data}} \), we are at the global optimum. It says nothing about the dynamics of reaching that state.
GAN training involves finding a saddle point of a non-convex, non-concave objective using alternating stochastic gradient updates. Such dynamical systems are prone to pathologies that simple minimization avoids, including: (i) Limit cycles, where the generator and discriminator chase each other in circles (rotational dynamics) without improving; (ii) Divergence, where gradients grow uncontrollably; and (iii) Mode collapse, where the generator maps all latent codes to a single ”safe” output that fools the discriminator, satisfying the local objective but failing to capture the full diversity of the data distribution.
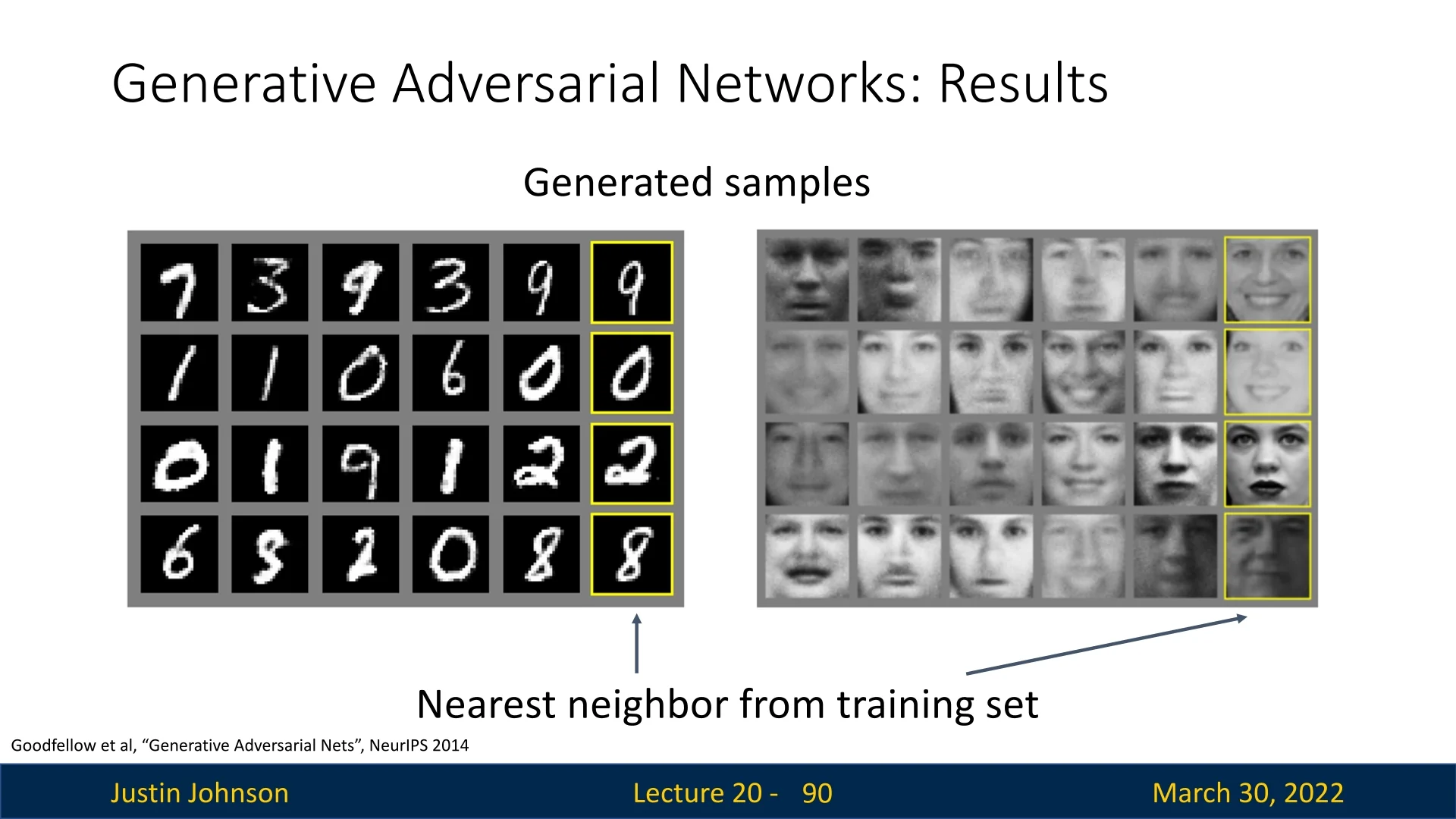
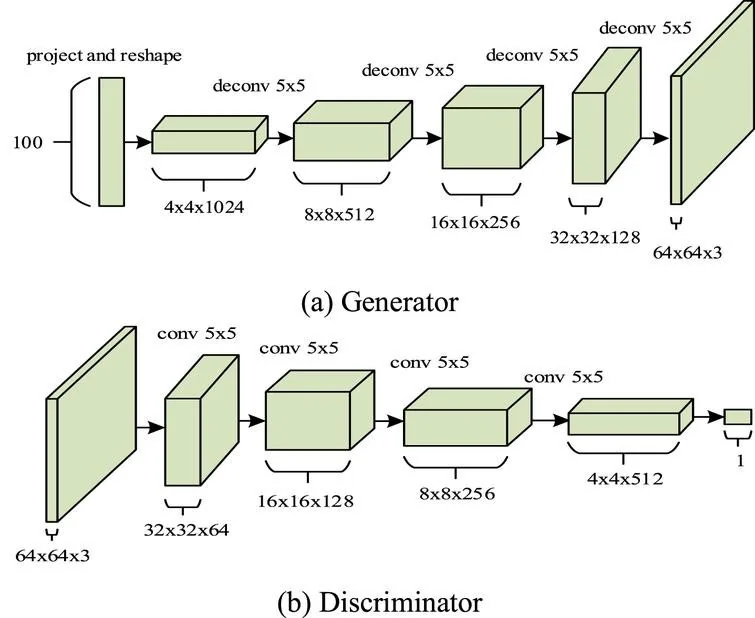
20.5 GANs in Practice: From Early Milestones to Modern Advances
20.5.1 The Original GAN (2014)
In their seminal work [180], Goodfellow et al. demonstrated that GANs could be trained to synthesize digits similar to MNIST and low-resolution human faces. While primitive by today’s standards, this was a significant leap: generating samples that look realistic without explicitly modeling likelihoods.
20.5.2 Deep Convolutional GAN (DCGAN)
The Deep Convolutional GAN (DCGAN) architecture, proposed by Radford et al. [495], marked a significant step toward stabilizing GAN training and improving the visual quality of generated images. Unlike the original fully connected GAN setup, DCGAN leverages the power of convolutional neural networks to better model image structure and achieve more coherent generations.
Architectural Innovations and Design Principles
- Convolutions instead of Fully Connected Layers: DCGAN eliminates dense layers at the input and output of the networks. Instead, it starts from a low-dimensional latent vector \( \mathbf {z} \sim \mathcal {N}(0, I) \) and progressively upsamples it through a series of transposed convolutions (also called fractional-strided convolutions) in the generator. This preserves spatial locality and improves feature learning.
- Strided Convolutions (Downsampling): The discriminator performs downsampling using strided convolutions rather than max pooling. This approach allows the network to learn its own spatial downsampling strategy rather than rely on a hand-designed pooling operation, thereby improving gradient flow and learning stability.
-
Fractional-Strided Convolutions (Upsampling): In the generator, latent codes are transformed into images through a series of transposed convolutions. These layers increase the spatial resolution of the feature maps while learning spatial structure, enabling the model to produce high-resolution outputs from compact codes.
- Batch Normalization: Applied in both the generator and discriminator (except the generator’s output layer and discriminator’s input layer), batch normalization smooths the learning dynamics and helps mitigate issues like mode collapse. It also reduces internal covariate shift, allowing higher learning rates and more stable convergence.
- Activation Functions: The generator uses ReLU activations in all layers except the output, which uses tanh to map values into the \([-1, 1]\) range. The discriminator uses LeakyReLU activations throughout, which avoids dying neuron problems and provides gradients even for negative inputs.
- No Pooling or Fully Connected Layers: The absence of pooling layers and fully connected components ensures the entire network remains fully convolutional, further reinforcing locality and translation equivariance.
Why it Works These design choices reflect the successful architectural heuristics of supervised CNNs (e.g., AlexNet, VGG) but adapted to the generative setting. The convolutional hierarchy builds up spatially coherent features, while batch normalization and careful activation design help maintain gradient signal throughout training. As a result, DCGANs are capable of producing high-quality samples on natural image datasets with far greater stability than the original GAN formulation.
Latent Space Interpolation One striking property of DCGAN is that interpolating between two latent codes \( \mathbf {z}_1 \) and \( \mathbf {z}_2 \) leads to smooth transitions in image space: \[ G((1-\alpha )\mathbf {z}_1 + \alpha \mathbf {z}_2), \quad \alpha \in [0, 1] \]
Latent Vector Arithmetic
DCGAN also revealed that semantic attributes can be disentangled in the latent space \( \mathbf {z} \). Consider the following operation:
\[ \mbox{smiling man} \approx \underbrace { \mbox{mean}(\mathbf {z}_{\mbox{smiling women}}) }_{\mbox{attribute: smile}} - \underbrace { \mbox{mean}(\mathbf {z}_{\mbox{neutral women}}) }_{\mbox{remove woman identity}} + \underbrace { \mbox{mean}(\mathbf {z}_{\mbox{neutral men}}) }_{\mbox{add male identity}} \]
A similar example uses glasses as a visual attribute: \[ \mathbf {z}_{\mbox{woman with glasses}} = \mathbf {z}_{\mbox{man with glasses}} - \mathbf {z}_{\mbox{man without glasses}} + \mathbf {z}_{\mbox{woman without glasses}} \]
Evaluating Generative Adversarial Networks (GANs)
Evaluating generative adversarial networks (GANs) remains one of the most important (and still imperfectly solved) problems in generative modeling. Unlike likelihood-based models (e.g., VAEs), standard GAN training does not yield a tractable scalar objective such as \(\log p_\theta (x)\) that can be directly used for model selection. Instead, as derived in the previous section, GANs optimize a minimax objective whose theoretical global optimum forces the generator to perfectly recover the data distribution (\(p_G = p_{\mbox{data}}\)), thereby minimizing the Jensen-Shannon Divergence (JSD).
Ideally, reaching this global minimum would satisfy all evaluation needs simultaneously. In practice, however, we must evaluate the generator’s partial success along three distinct axes, each rooted in the min-max formulation:
- 1.
- Fidelity (Realism): Do individual samples look real?
Min-Max mechanism: Enforced by the discriminator \(D\). To minimize JSD, the generator must ensure \(p_G(x)\) is non-zero only where \(p_{\mbox{data}}(x)\) is high. If \(G\) generates samples outside the manifold of real data, the optimal discriminator \(D^*\) easily identifies and penalizes them. - 2.
- Diversity / Coverage: Does the model represent all modes of the
data?
Min-Max mechanism: Theoretically mandated by the condition \(p_G = p_{\mbox{data}}\). The JSD is only zero if \(G\) covers every mode of the target distribution with the correct density. (In practice, however, optimization instability often leads to mode collapse, where \(G\) captures only a single mode to satisfy \(D\)). - 3.
- Semantic Correctness: (Optional) Does the model respect
conditioning?
Min-Max mechanism: In conditional GANs, the adversarial game extends to joint distributions. The discriminator forces \(p_G(x,y)\) to match \(p_{\mbox{data}}(x,y)\), ensuring that generated samples \(x\) are not just realistic, but correctly aligned with their labels \(y\).
Since the training loss value (ideally \(-\log 4\)) is often uninformative about which of these properties is being satisfied or violated, modern practice relies on a bundle of external checks and scores [543, 400].
A practical rule: metrics are only comparable under the same protocol Absolute scores (especially FID/KID) are generally not portable across different datasets, resolutions, feature extractors, or preprocessing pipelines. Therefore, whenever you report a quantitative score, you should also report the evaluation protocol: the real split used (train vs. held-out test), image resolution, number of generated samples, the feature extractor \(\phi (\cdot )\), and the exact preprocessing (in particular, resizing and cropping policy). In practice, protocol differences can easily cause score swings that are comparable to (or larger than) architectural gains.
Qualitative vs. quantitative evaluation We divide evaluation methods into two main categories: qualitative (human judgment, nearest-neighbor checks) and quantitative (feature-space distribution metrics such as IS, FID, KID, and precision/recall).
Qualitative Evaluation Methods
Manual inspection and preference ranking The simplest evaluation technique is visual inspection of samples. Human judges may rate realism, compare images side-by-side, or choose which model produces higher-quality samples.
In practice, this is often implemented via crowd-sourcing (e.g., Amazon Mechanical Turk) or via blinded pairwise preference tests [543]. The advantage is sensitivity to “semantic failures” that scalar metrics may miss (odd textures, broken geometry, repeated artifacts). The drawbacks are that it is subjective, expensive, and difficult to scale to large sweeps or to reproduce exactly.
Nearest-neighbor retrieval (memorization / leakage sanity check) A standard diagnostic is to test whether generated samples are near-duplicates of training examples. Given a generated image \(x_g\), retrieve its nearest neighbor among a reference set of real images \(\{x_r\}\) using a perceptual similarity measure.
Important: Pixel-space \(\ell _2\) is typically misleading (tiny translations can dominate \(\ell _2\) while being visually negligible), so in practice one uses deep features (e.g., Inception/DINO/CLIP embeddings) or perceptual distances such as LPIPS [778]. Qualitatively inspecting pairs \((x_g,\mathrm {NN}(x_g))\) can reveal direct copying. However, note the asymmetry of this test: “not identical to a training image” is not a proof of generalization; it is only a guardrail against the most obvious memorization failure modes.
Quantitative Evaluation Methods
Most modern metrics compare distributions of embeddings Many widely used GAN metrics begin by embedding images with a fixed, pretrained feature extractor \(\phi (\cdot )\in \mathbb {R}^d\) (classically Inception-v3 pool3 features). One then compares the empirical distributions of real embeddings \(\{\phi (x_r)\}\) and generated embeddings \(\{\phi (x_g)\}\). This is both a strength and a limitation: the metric becomes sensitive to the semantics captured by \(\phi \), and insensitive to aspects \(\phi \) ignores. This dependence is especially important under domain shift (e.g., medical images), where ImageNet-pretrained features may be a weak proxy for perceptual similarity.
Inception Score (IS) Proposed by [543], the Inception Score uses a pretrained classifier \(p_\phi (y\mid x)\) to reward two properties: (i) confidence on each generated sample (low conditional entropy \(H(Y\mid X)\)), and (ii) label diversity across samples (high marginal entropy \(H(Y)\)). Let \(p_\phi (y)=\mathbb {E}_{x\sim p_G}[p_\phi (y\mid x)]\). Then \[ \mathrm {IS} \;=\; \exp \!\left ( \mathbb {E}_{x\sim p_G}\!\left [ D_{\mathrm {KL}}\!\big (p_\phi (y\mid x)\,\|\,p_\phi (y)\big ) \right ]\right ). \] While IS historically appears in many papers, it is often de-emphasized in modern reporting because it has several structural limitations:
- No real-vs.-fake comparison: IS depends only on generated samples, so it can increase even if samples drift away from the true data distribution.
- Classifier and label-set bias: its meaning depends on whether the pretrained classifier is appropriate for the domain.
- Can miss intra-class mode collapse: generating one “prototype” per class can yield a strong IS while having poor within-class diversity.
Fréchet Inception Distance (FID) The Fréchet Inception Distance (FID) [218] improves upon IS by directly comparing real and generated feature distributions. Given real images \(\{x_r\}\) and generated images \(\{x_g\}\), compute embeddings \(u=\phi (x_r)\) and \(v=\phi (x_g)\), estimate empirical means and covariances \((\mu _r,\Sigma _r)\) and \((\mu _g,\Sigma _g)\), and define the squared 2-Wasserstein (Fréchet) distance between the corresponding Gaussians: \[ \mathrm {FID} \;=\; \|\mu _r-\mu _g\|_2^2 \;+\; \mathrm {Tr}\!\Big ( \Sigma _r+\Sigma _g - 2\big (\Sigma _r^{1/2}\,\Sigma _g\,\Sigma _r^{1/2}\big )^{1/2} \Big ). \]
Intuitively, the mean term \(\|\mu _r-\mu _g\|_2^2\) captures a shift/bias between the feature clouds, while the covariance term captures mismatch in spread and correlations (often aligned with diversity and mode coverage). This real-vs.-fake distribution comparison is the main reason FID became a de facto standard.
How to interpret FID (and why “typical ranges” are only rough)
- Lower is better: smaller FID indicates closer alignment between real and generated feature distributions under \(\phi \).
- Non-zero even for real-vs.-real: if you compute FID between two finite real sample sets, it is typically non-zero due to sampling noise.
- Context-dependent scale: absolute values depend strongly on dataset, resolution, and protocol; the safest use of FID is relative comparison under a fixed evaluation pipeline.
FID limitations and implementation pitfalls (often the main source of confusion)
- Second-order (Gaussian) summary: FID matches only first and second moments of \(\phi (x)\); real feature distributions are typically multi-modal, so \((\mu ,\Sigma )\) is a coarse approximation.
- Preprocessing sensitivity: resizing interpolation, cropping, and normalization can measurably change FID. For fair comparisons, treat preprocessing as part of the metric definition (“CleanFID-style” discipline: fixed, explicit preprocessing and extractor).
- Finite-sample effects: FID is a biased estimator with nontrivial variance at small sample sizes; comparisons are most meaningful when computed with a large, fixed sample budget and (ideally) repeated across random seeds/splits.
- Domain mismatch (feature-extractor bias): Inception features encode ImageNet semantics. For domains far from ImageNet, it is common to replace \(\phi \) with a domain-relevant encoder (supervised or self-supervised), but then scores become extractor-specific and must not be compared across different choices of \(\phi \).
A Note on Reconstruction Metrics (PSNR, SSIM, LPIPS) Readers coming from classical image restoration (denoising, deblurring, super-resolution) often report PSNR or SSIM. These are paired (reference-based) metrics: they require a pixel-aligned ground-truth target \(x\) and a prediction \(\hat {x}\). This makes them appropriate for supervised tasks (where a single “correct” answer exists) but fundamentally mismatched to unconditional GAN synthesis (where no unique target exists) and often misleading even for conditional GANs.
-
Peak Signal-to-Noise Ratio (PSNR). PSNR is simply a logarithmic rescaling of the pixelwise Mean Squared Error (MSE): \[ \mathrm {PSNR}(x,\hat {x}) = 10\log _{10}\!\left (\frac {\mathrm {MAX}_I^2}{\mathrm {MSE}(x,\hat {x})}\right ), \] where \(\mathrm {MAX}_I\) is the maximum dynamic range (e.g., 255).
Why it fails for GANs: MSE relies on pixel-wise \(\ell _2\) distance. It treats a tiny spatial shift (e.g., a nose moved by 1 pixel) as a massive error, yet it rewards blurring (averaging) because the mean of many plausible edges minimizes the squared error. GANs, designed to produce sharp, hallucinated details, often have poor PSNR despite superior perceptual quality.
-
Structural Similarity Index (SSIM). SSIM attempts to quantify perceptual similarity by comparing local statistics of image patches rather than raw pixels. For two patches \(x\) and \(\hat {x}\), SSIM is the product of three terms: \[ \mathrm {SSIM}(x,\hat {x}) = \underbrace {l(x,\hat {x})^\alpha }_{\mbox{Luminance}} \cdot \underbrace {c(x,\hat {x})^\beta }_{\mbox{Contrast}} \cdot \underbrace {s(x,\hat {x})^\gamma }_{\mbox{Structure}} \] 1. Why do these terms match human perception? SSIM maps statistical moments to visual concepts:
- Luminance (Mean \(\mu \)): The average pixel intensity \(\mu _x\) corresponds directly to the patch’s brightness. A global lighting shift affects \(\mu \) but leaves the content intact.
- Contrast (Variance \(\sigma \)): The standard deviation \(\sigma _x\) measures the signal amplitude. A flat grey patch has \(\sigma =0\) (no contrast), while a sharp edge has high \(\sigma \). Blurring acts as a low-pass filter, reducing \(\sigma \), which SSIM penalizes as a loss of contrast.
- Structure (Covariance \(\sigma _{x\hat {x}}\)): The normalized correlation measures if the patterns align (e.g., do gradients point in the same direction?) regardless of their absolute brightness or amplitude.
2. Why SSIM fails for Semantic Realism: While better than PSNR, SSIM is still a low-level statistic. It checks if local edges align, not if the image makes sense. A generated face with distorted anatomy (e.g., an eye on the chin) might have excellent local contrast and texture statistics (high SSIM if aligned to a reference), while being semantically broken. Conversely, a plausible dog generated in a slightly different pose than the reference will suffer a huge penalty.
LPIPS: Perceptual Similarity in Deep Feature Space To bridge the gap between pixel metrics and human perception, LPIPS (Learned Perceptual Image Patch Similarity) [778] measures distance in the activation space of a pre-trained deep network (e.g., VGG or AlexNet). \[ \mathrm {LPIPS}(x,\hat {x}) = \sum _{\ell } \| w_\ell \odot (\psi _\ell (x) - \psi _\ell (\hat {x})) \|_2^2 \] Unlike PSNR, which sees a ”bag of pixels,” LPIPS sees ”hierarchy of features.” It correctly identifies that a sharp, texture-rich image is closer to reality than a blurry average, even if the pixels don’t align perfectly.
Other Quantitative Metrics (Complements, Not Replacements) Since unconditional GANs cannot use paired metrics, we rely on distributional metrics to diagnose specific failure modes.
-
Precision and Recall (Manifold Approximation) [541]. These metrics separate Fidelity (Precision) from Coverage (Recall).
How are they measured without the true manifold? Since we cannot know the true high-dimensional manifold, we approximate it using \(k\)-Nearest Neighbors (\(k\)-NN) balls around the available data samples in feature space.
- Precision (Quality): What % of generated samples fall within the \(k\)-NN balls of the real data? (If low: generating garbage).
- Recall (Diversity): What % of real samples fall within the \(k\)-NN balls of the generated data? (If low: mode collapse).
-
Kernel Inception Distance (KID) [45]. KID is a non-parametric alternative to FID. Instead of assuming feature embeddings follow a Gaussian distribution, KID measures the squared Maximum Mean Discrepancy (MMD) between the real and generated distributions in a reproducing kernel Hilbert space (RKHS).
1. Feature Embeddings (\(X\) and \(Y\)). Like FID, KID operates in the feature space of a pre-trained network \(\phi (\cdot )\) (usually Inception-v3). We define two sets of embeddings: \[ X = \{\phi (x_r^{(i)})\}_{i=1}^m \quad (\mbox{Real}), \qquad Y = \{\phi (x_g^{(j)})\}_{j=1}^n \quad (\mbox{Generated}). \] Note that the sample sizes \(m\) and \(n\) need not be equal. This is practically useful when the test set size is fixed (e.g., \(m=10,000\)) but you wish to evaluate a smaller batch of generated samples (\(n=2,000\)) for efficiency.
2. The Metric: Unbiased MMD. KID compares these sets using a polynomial kernel function, typically \(k(u,v) = (\frac {1}{d}u^\top v + 1)^3\). The metric is computed via an unbiased estimator composed of three terms: \[ \widehat {\mathrm {KID}} = \underbrace {\frac {1}{m(m-1)}\sum _{i\neq i'} k(x_i, x_{i'})}_{\mbox{Average Real--Real Similarity}} \;+\; \underbrace {\frac {1}{n(n-1)}\sum _{j\neq j'} k(y_j, y_{j'})}_{\mbox{Average Gen--Gen Similarity}} \;-\; \underbrace {\frac {2}{mn}\sum _{i=1}^m \sum _{j=1}^n k(x_i, y_j)}_{\mbox{Average Real--Gen Similarity}} \]
3. Intuition and Advantages. Conceptually, the formula measures ”cohesion vs. separation”: if the distributions match, the average cross-similarity (real vs. generated) should equal the average self-similarity (real vs. real).
- Unbiasedness: The primary advantage of KID over FID is that its estimator is unbiased. FID systematically overestimates the distance when \(N\) is small (bias \(\propto 1/N\)). KID’s expected value equals the true population distance regardless of sample size.
- Practical Use: This makes KID the standard choice for **small datasets**, few-shot generation, or limited compute budgets where generating 50,000 samples for stable FID is infeasible.
-
Classifier Two-Sample Tests (C2ST). This involves training a new, separate binary classifier to distinguish Real vs. Fake samples after the GAN is trained.
- If Accuracy \(\approx \) 50%: The distributions are indistinguishable (Perfect GAN).
- If Accuracy \(\gg \) 50%: The classifier can spot the fakes.
Difference from GAN Discriminator: The GAN discriminator is part of the dynamic training game (moving target). C2ST is a static ”post-game referee” that provides a sanity check on whether the final result is truly indistinguishable.
- Geometry Score (GS) [290]. While FID measures density, GS measures Topology (shape complexity). It builds a graph of the data manifold and compares topological features like ”number of holes” or ”connected components”. Intuition: If the real data forms a single connected ring (like a donut) but the GAN generates two disconnected blobs, FID might be low (blobs are in the right place), but GS will penalize the broken connectivity (wrong topology).
Optional but important when editing matters: Latent-Space Diagnostics Metrics like FID evaluate the destination (the final distribution of images). They do not tell us about the journey—specifically, whether the latent space is well-structured for editing and interpolation. For models like StyleGAN, we use Perceptual Path Length (PPL) [278] to quantify the ”smoothness” of the latent manifold.
The Intuition: Smooth vs. Rugged Landscapes. Imagine walking in a straight line through the latent space. In a disentangled (good) space, a small step results in a small, consistent visual change (e.g., a face slowly turning). In an entangled (bad) space, the same small step might cause sudden, erratic jumps (e.g., a face suddenly changing identity or artifacts appearing and disappearing). PPL measures this ”bumpiness”.
How is it computed?
- 1.
- Interpolate: Pick two latent codes \(z_1, z_2\) and take a tiny step \(\epsilon \) along the path between them (usually using spherical interpolation, slerp).
- 2.
- Generate: Decode the images at the start and end of this tiny step: \(x = G(z(t))\) and \(x' = G(z(t+\epsilon ))\).
- 3.
- Measure: Calculate the perceptual distance \(d = \mbox{LPIPS}(x, x')\).
- 4.
- Normalize: PPL is the expected value of this distance normalized by the step size \(\epsilon ^2\).
Interpretation:
- Low PPL (Good): The latent space is perceptually uniform. Changes in latent values map linearly to changes in visual appearance, making the model reliable for animation and editing.
- High PPL (Bad): The latent space contains ”hidden” non-linearities or singularities where the image changes drastically (or breaks) over short distances.
Limitations and Practical Guidelines
Robust evaluation requires Protocol Discipline. Absolute scores are meaningless without context.
- Report the Protocol: Always specify resolution, feature extractor (e.g., Inception-v3), and resizing method (CleanFID).
- Triangulate: Never rely on one number. Pair a distributional metric (FID/KID) with a diagnostic metric (Precision/Recall).
- Qualitative Guardrails: Always visually inspect nearest neighbors. A perfect FID of 0.0 means nothing if the model simply memorized the training set.
Summary Evaluating GANs is difficult precisely because there is no single, universally meaningful scalar objective. In practice, the most reliable approach is protocol discipline plus metric triangulation: report a real-vs.-fake distribution metric (FID or KID), decompose fidelity vs. coverage (precision–recall), and keep qualitative sanity checks (inspection and nearest neighbors). When Inception features are a poor fit for the domain, the feature extractor must be treated as part of the metric definition, and comparisons should be restricted accordingly.
20.5.3 GAN Explosion
These results sparked rapid growth in the GAN research landscape, with hundreds of new papers and variants proposed every year. For a curated (and still growing) collection of GAN papers, see: The GAN Zoo.
Next Steps: Improving GANs While the original GAN formulation [180] introduced a powerful framework, it often suffers from instability, vanishing gradients, and mode collapse during training. These issues led to a wave of improvements that we now explore in the following sections. Notable directions include:
- Wasserstein GAN (WGAN) — replaces the Jensen–Shannon-based loss with the Earth Mover’s (Wasserstein) distance for smoother gradients.
- WGAN-GP — introduces a gradient penalty to enforce Lipschitz constraints without weight clipping.
- StyleGAN / StyleGAN2 — enables high-resolution image synthesis with disentangled and controllable latent spaces.
- Conditional GANs (cGANs) — allows conditioning the generation process on labels, text, or other modalities.
These innovations make GANs more robust, interpretable, and scalable — paving the way for practical applications in vision, art, and science.
20.5.4 Wasserstein GAN (WGAN): Earth Mover’s Distance
While original GANs achieved impressive qualitative results, their training can be highly unstable and sensitive to hyperparameters. A key theoretical issue is that, under an optimal discriminator, the original minimax GAN objective reduces to a constant plus a Jensen–Shannon (JS) divergence term between \(p_{\mbox{data}}\) and \(p_G\) [180]. In high-dimensional settings where the two distributions often lie on (nearly) disjoint low-dimensional manifolds, this JS-based perspective helps explain why the learning signal can become weak or poorly behaved. Below, we revisit this failure mode and then introduce Wasserstein GAN (WGAN) [14], which replaces JS with the Wasserstein-1 (Earth Mover) distance to obtain a smoother, geometry-aware objective.
Supports and Low-Dimensional Manifolds
- Support of a distribution: The subset of space where the distribution assigns non-zero probability. In high-dimensional data like images, real samples lie on or near a complex, low-dimensional manifold (e.g., the “face manifold” of all possible human faces).
- Generator manifold: Similarly, the generator’s outputs \(G(z)\) with \(z \sim p(z)\) occupy their own manifold. Initially, the generator manifold often lies far from the data manifold.
Why the JS Divergence Fails in High Dimensions In the original minimax GAN game, if the discriminator is optimized for a fixed generator, the value function can be written as a constant plus a Jensen–Shannon divergence term [180]: \[ \max _D \; V(G,D) = -\log 4 + 2\,JS\!\left (p_{\mbox{data}} \,\|\, p_G\right ). \] Thus, improving the generator in the idealized setting corresponds to reducing a JS-based discrepancy between \(p_{\mbox{data}}\) and \(p_G\). However, when these distributions have disjoint support, this discrepancy saturates and yields a poorly behaved learning signal:
- Early training (negligible overlap): The generator typically produces unrealistic outputs, so \(p_G\) has little overlap with \(p_{\mbox{data}}\). Ideally, we want a gradient that points towards the data. However, the JS divergence saturates to a constant (\(\log 2\)) when supports are disjoint, providing no smooth notion of “distance” to guide the generator.
- Weak or unreliable generator signal near an optimal discriminator: As the discriminator becomes very accurate, its outputs saturate (\(D(x)\approx 1\) on real, \(D(G(z))\approx 0\) on fake). This can yield vanishing or highly localized gradients for the generator, making training brittle and contributing to mode collapse.
Non-Saturating Trick: A Partial Fix. To mitigate immediate vanishing gradients, Goodfellow et al. [180] proposed replacing the minimax generator objective with a different (but still consistent) surrogate.
In the original formulation, the generator minimizes the probability of the discriminator being correct: \begin {equation} \mathcal {L}_G^{\mbox{minimax}} = \mathbb {E}_{z \sim p(z)}[\log (1 - D(G(z)))]. \end {equation} When the discriminator is strong (common early in training), \(D(G(z)) \approx 0\). In this region, the function \(\log (1 - x)\) saturates—it becomes flat, yielding near-zero gradients.
The non-saturating alternative instead maximizes the discriminator’s output on fake samples: \begin {equation} \max _G\;\mathbb {E}_{z \sim p(z)}[\log D(G(z))] \quad \Longleftrightarrow \quad \min _G\;\mathcal {L}_G^{\mbox{NS}} = -\mathbb {E}_{z \sim p(z)}[\log D(G(z))]. \end {equation} Why it helps: Although the optimum point theoretically remains the same, the gradient dynamics differ. The function \(-\log (x)\) rises sharply as \(x \to 0\). This ensures the generator receives a strong gradient signal precisely when it is performing poorly (i.e., when \(D(G(z)) \approx 0\)), kickstarting the learning process.
The Need for a Better Distance Metric Ultimately, the issue is not with the choice of generator loss formulation alone — it’s with the divergence measure itself. Wasserstein GANs (WGANs) address this by replacing JS with the Wasserstein-1 distance, also known as the Earth Mover’s Distance (EMD). Unlike JS, the Wasserstein distance increases smoothly as the distributions move apart and remains informative even when they are fully disjoint. It directly measures how much and how far the probability mass needs to be moved to align \( p_G \) with \( p_{\mbox{data}} \). As a result, WGANs produce gradients that are:
- Typically less prone to saturation than JS-based objectives when the critic is trained near its optimum.
- More reflective of distributional geometry (how mass must move), rather than only separability.
- Better aligned with incremental improvements in sample quality, often yielding smoother and more stable optimization in practice.
This theoretical improvement forms the basis of WGANs, laying the foundation for more stable and expressive generative training — even before considering architectural or loss refinements like gradient penalties in WGAN-GP [194], which we’ll cover later as well.
Wasserstein-1 Distance: Transporting Mass The Wasserstein-1 distance — also called the Earth Mover’s Distance (EMD) — quantifies how much “mass” must be moved to transform the generator distribution \( p_G \) into the real data distribution \( p_{\mbox{data}} \), and how far that mass must travel. Formally: \[ W(p_{\mbox{data}}, p_G) = \inf _{\gamma \in \Pi (p_{\mbox{data}}, p_G)} \, \mathbb {E}_{(x, y) \sim \gamma } \left [ \|x - y\| \right ] \]
Here:
- \( \gamma (x, y) \) is a transport plan, i.e., a joint distribution describing how much mass to move from location \( y \sim p_G \) to location \( x \sim p_{\mbox{data}} \).
- The set \(\Pi (p_{\mbox{data}}, p_G)\) contains all valid couplings—that is, joint distributions \(\gamma (x, y)\) whose marginals match the source and target distributions. Concretely, \(\gamma \) must satisfy: \begin {equation} \int \gamma (x, y) \, dy = p_{\mbox{data}}(x) \quad \mbox{and} \quad \int \gamma (x, y) \, dx = p_G(y). \end {equation} (In discrete settings, these integrals become sums). This constraint ensures mass conservation: no probability mass is created or destroyed; it is simply moved from \(y\) to \(x\).
- The infimum (\( \inf \)) takes the best (lowest cost) over all possible plans \( \gamma \in \Pi \).
- The cost function \( \|x - y\| \) reflects how far one must move a unit of mass from \( y \) to \( x \). It is often Euclidean distance, but other choices are possible.
Example: Optimal Transport Plans as Joint Tables To see this in action, consider a simple example in 1D:
- Generator distribution \( p_G \): 0.5 mass at \( y_1 = 0 \), and 0.5 at \( y_2 = 4 \).
- Data distribution \( p_{\mbox{data}} \): 0.5 mass at \( x_1 = 2 \), and 0.5 at \( x_2 = 3 \).
Each plan defines a joint distribution \( \gamma (x, y) \) specifying how much mass to move between source and target locations.
Plan 1 (Optimal): \[ \gamma _{\mbox{plan 1}}(x, y) = \begin {array}{c|cc} & y=0 & y=4 \\ \hline x=2 & 0.5 & 0.0 \\ x=3 & 0.0 & 0.5 \\ \end {array} \quad \Rightarrow \quad \mbox{Cost} = 0.5\cdot |2{-}0| + 0.5\cdot |3{-}4| = 1 + 0.5 = \boxed {1.5} \]
Plan 2 (Suboptimal): \[ \gamma _{\mbox{plan 2}}(x, y) = \begin {array}{c|cc} & y=0 & y=4 \\ \hline x=2 & 0.0 & 0.5 \\ x=3 & 0.5 & 0.0 \\ \end {array} \quad \Rightarrow \quad \mbox{Cost} = 0.5\cdot |3{-}0| + 0.5\cdot |2{-}4| = 1.5 + 1 = \boxed {2.5} \]
Plan 3 (Mixed): \[ \gamma _{\mbox{plan 3}}(x, y) = \begin {array}{c|cc} & y=0 & y=4 \\ \hline x=2 & 0.25 & 0.25 \\ x=3 & 0.25 & 0.25 \\ \end {array} \quad \Rightarrow \quad \mbox{Cost} = \sum \gamma (x, y)\cdot |x{-}y| = \boxed {2.0} \]
Each table represents a valid joint distribution \( \gamma \in \Pi (p_{\mbox{data}}, p_G) \), since the row and column sums match the marginal probabilities. The Wasserstein-1 distance corresponds to the cost of the optimal plan, i.e., the one with lowest total transport cost.
- Meaningful even with disjoint support: Unlike JS (which saturates at \(\log 2\) under disjoint support in the idealized analysis), Wasserstein-1 continues to vary with the geometric separation between distributions.
- Captures geometric mismatch: It does not merely say “different”; it encodes how far probability mass must move under an optimal coupling.
- Potentially informative signal early in training: When the critic is trained near its optimum and the Lipschitz constraint is controlled, the resulting gradients can remain useful even when \(p_G\) is far from the data manifold.
From Intractable Transport to Practical Training The Wasserstein-1 distance offers a theoretically sound objective that avoids the saturation problems of JS divergence. However, its original definition involves a highly intractable optimization over all possible joint couplings: \[ W(p_{\mbox{data}}, p_G) = \inf _{\gamma \in \Pi (p_{\mbox{data}}, p_G)} \, \mathbb {E}_{(x, y) \sim \gamma } \left [ \|x - y\| \right ] \] Computing this infimum directly is not feasible for high-dimensional distributions like images.
The Kantorovich–Rubinstein duality makes the problem tractable by recasting it as: \[ W(p_{\mbox{data}}, p_G) = \sup _{\|f\|_L \leq 1} \left ( \mathbb {E}_{x \sim p_{\mbox{data}}} [f(x)] - \mathbb {E}_{\tilde {x} \sim p_G} [f(\tilde {x})] \right ), \] where the supremum is taken over all 1-Lipschitz functions \( f \colon \mathcal {X} \to \mathbb {R} \).
What These Expectations Mean in Practice In actual training, we do not have access to the full distributions \( p_{\mbox{data}} \) and \( p_G \), but only to samples. The expectations are therefore approximated by empirical means over minibatches: \[ \mathbb {E}_{x \sim p_{\mbox{data}}}[f(x)] \;\approx \; \frac {1}{m} \sum _{i=1}^{m} f(x^{(i)}), \qquad \mathbb {E}_{\tilde {x} \sim p_G}[f(\tilde {x})] \;\approx \; \frac {1}{m} \sum _{i=1}^{m} f(G(z^{(i)})), \] where:
- \( \{x^{(i)}\}_{i=1}^m \) is a minibatch sampled from the training dataset \( p_{\mbox{data}} \).
- \( \{z^{(i)}\}_{i=1}^m \sim p(z) \), typically \( \mathcal {N}(0, I) \), is a batch of latent codes.
- \( \tilde {x}^{(i)} = G(z^{(i)}) \) are the generated images.
How the Training Works (Maximize vs. Minimize). In WGAN, the critic \(f_w\) (parameterized by weights \(w\)) is trained to approximate the dual optimum by widening the score gap between real and fake data.
- 1.
- The Critic Loss (Implementation View): Since deep learning frameworks typically minimize loss functions, we invert the dual objective. We minimize the difference: \begin {equation} \mathcal {L}_{\mbox{critic}} = \underbrace {\mathbb {E}_{z \sim p(z)}[f_w(G(z))]}_{\mbox{Score on Fake}} - \underbrace {\mathbb {E}_{x \sim p_{\mbox{data}}}[f_w(x)]}_{\mbox{Score on Real}}. \end {equation} Minimizing this quantity is equivalent to maximizing the score on real data while minimizing it on fake data.
- 2.
- The Generator Loss: The generator is updated to minimize the critic’s score on its output (effectively trying to move its samples “uphill” along the critic’s value surface): \begin {equation} \mathcal {L}_{\mbox{gen}} = -\mathbb {E}_{z \sim p(z)}[f_w(G(z))]. \end {equation}
Intuitively, the critic learns a scalar potential function whose slopes point towards the data manifold, and the generator moves its probability mass to follow these gradients.
Why This Makes Sense — Even if Samples Differ Sharply This training might appear unintuitive at first glance:
- We are not directly comparing real and fake images pixel-by-pixel.
- The generator might produce very different images (e.g., noise) from real data in early training.
Yet, the setup works because:
- The critic learns a scalar-valued function \( f(x) \) that assigns a meaningful score to each image, indicating how realistic it appears under the current critic.
- Even if two distributions have no overlapping support, the critic can still produce distinct outputs for each — preserving a non-zero mean score gap.
- The generator then improves by reducing this gap, pushing \( p_G \) closer to \( p_{\mbox{data}} \) in a distributional sense.
In other words, we do not require individual generated samples to match real ones — only that, on average, the generator learns to produce samples that fool the critic into scoring them similarly.
Summary WGAN training works by:
- 1.
- Using minibatch means to estimate expectations in the dual Wasserstein objective.
- 2.
- Leveraging the critic as a 1-Lipschitz scoring function trained to separate real from fake.
- 3.
- Providing stable, non-vanishing gradients even when real and generated distributions are far apart.
This principled approach turns adversarial training into a smooth, geometry-aware optimization process — and lays the foundation for further improvements like WGAN-GP.
Side-by-Side: Standard GAN vs. WGAN
| Component | Standard GAN | Wasserstein GAN (WGAN) |
|---|---|---|
| Objective | \( \begin {array}{l} \min _G \max _D \bigl [ \mathbb {E}_{x \sim p_{\mbox{data}}} \log D(x) \\ +\, \mathbb {E}_{z \sim p(z)} \log (1 - D(G(z))) \bigr ] \end {array} \) | \( \begin {array}{l} \min _G \max _{\|f\|_L \leq 1} \bigl [ \mathbb {E}_{x \sim p_{\mbox{data}}} f(x) \\ -\, \mathbb {E}_{z \sim p(z)} f(G(z)) \bigr ] \end {array} \) |
| Output Type | \( D(x) \in [0,1] \) (probability) | \( f(x) \in \mathbb {R} \) (score) |
| Interpretation | Probability \( x \) is real | Realism score for \( x \) |
| Training Signal | Jensen–Shannon divergence | Wasserstein-1 (Earth Mover) distance |
| Disjoint Supports | JS saturates to \( \log 2 \); gradients vanish | Distance remains informative (with Lipschitz critic) |
What’s Missing: Enforcing the 1-Lipschitz Constraint The dual WGAN formulation transforms the intractable Wasserstein distance into a solvable optimization problem: \[ W(p_{\mbox{data}}, p_G) = \sup _{\|f\|_L \leq 1} \left ( \mathbb {E}_{x \sim p_{\mbox{data}}}[f(x)] - \mathbb {E}_{x \sim p_G}[f(x)] \right ) \] However, this relies on a crucial condition: the function \( f \) must be 1-Lipschitz — that is, it cannot change too quickly: \[ |f(x_1) - f(x_2)| \leq \|x_1 - x_2\| \quad \forall x_1, x_2 \]
This constraint ensures that the critic’s output is smooth and bounded — a key requirement to preserve the validity of the dual formulation. Yet enforcing this constraint precisely over a deep neural network is non-trivial. To address this, Arjovsky et al. [14] introduce a simple approximation: weight clipping.
Weight Clipping: A Crude Approximation After each gradient update during training, every parameter \( w \) in the critic is constrained to lie within a compact range: \[ w \leftarrow \mbox{clip}(w, -c, +c) \quad \mbox{with} \quad c \approx 0.01 \]
The rationale is that limiting the range of weights constrains the magnitude of the output changes, thereby approximating a 1-Lipschitz function. If the weights are small, then the critic function \( f(x) \) cannot change too rapidly with respect to changes in \( x \).
Benefits of WGAN Despite using a crude approximation like weight clipping to enforce the 1-Lipschitz constraint, Wasserstein GANs (WGAN) demonstrate compelling improvements over standard GANs:
- More interpretable training signal (often): When the critic is trained near its optimum, the WGAN critic loss frequently correlates better with generator progress than standard GAN discriminator losses, making it a more practical monitoring metric.
- Smoother optimization in challenging regimes: Because Wasserstein-1 varies continuously with distributional shifts (including disjoint support), WGAN can yield less saturated and more stable gradients than JS-based objectives, especially early in training.
- Reduced risk of mode collapse (not eliminated): By encouraging the generator to reduce a transport-based discrepancy rather than only improving separability, WGAN training can make collapse less likely in practice, though it does not guarantee full mode coverage.
Limitations of Weight Clipping in Practice While simple to implement, weight clipping is an imprecise and inefficient method for enforcing the 1-Lipschitz constraint. It introduces multiple issues that degrade both the expressiveness of the critic and the overall training dynamics:
- Reduced expressivity: Weight clipping constrains each parameter of the critic network to lie within a small range (e.g., \( [-0.01, 0.01] \)). This effectively flattens the critic’s function space, especially in deeper architectures. The resulting networks tend to behave like near-linear functions, as layers with small weights compound to produce low-variance outputs. Consequently, the critic struggles to capture meaningful variations between real and generated data — particularly in complex image domains — leading to weak or non-informative gradients for the generator.
-
Fragile gradient propagation: Gradient-based learning relies on consistent signal flow through layers. When weights are clipped, two opposing issues can arise:
- If weights are too small, the gradients shrink with each layer — leading to vanishing gradients, especially in deep networks.
- If weights remain non-zero but unevenly distributed across layers, activations can spike, causing exploding gradients in certain directions due to unbalanced Jacobians.
These effects are particularly problematic in ReLU-like networks, where clipping reduces activation diversity and gradient feedback becomes increasingly unreliable.
- Training instability and non-smooth loss: Empirical studies (e.g., Figure 4 in [14]) show that critics trained under clipping oscillate unpredictably. In some iterations, the critic becomes too flat to distinguish between real and fake inputs; in others, it becomes overly reactive to minor differences. This leads to high-variance Wasserstein estimates and erratic training curves. Worse, when the critic is underfit, the generator may receive biased or misleading gradients, preventing effective mode coverage or long-term convergence.
Despite these challenges, weight clipping served its purpose in the original WGAN: it provided a proof of concept that optimizing the Wasserstein-1 distance offers substantial advantages over traditional GAN losses. However, it quickly became apparent that a more robust and mathematically faithful mechanism was needed. This inspired Gulrajani et al. [194] to propose WGAN-GP — which enforces Lipschitz continuity via a smooth and principled gradient penalty, significantly improving stability and sample quality.
20.5.5 WGAN-GP: Gradient Penalty for Stable Lipschitz Enforcement
While WGAN introduced a major improvement by replacing the JS divergence with the Wasserstein-1 distance, its dual formulation relies on a key mathematical requirement: the critic \( f \colon \mathcal {X} \to \mathbb {R} \) must be 1-Lipschitz. In the original WGAN, this was enforced via weight clipping, which constrains parameters to a small interval. As discussed, clipping is a coarse proxy for Lipschitz control and often leads to underfitting (an overly simple critic) or brittle optimization.
To address this, Gulrajani et al. [194] proposed WGAN-GP, which replaces structural constraints on parameters with a differentiable gradient penalty that directly regularizes the critic’s input sensitivity in the region most relevant to training.
Theoretical Motivation: Lipschitz Continuity as “Controlled Sensitivity” A function \( f \) is 1-Lipschitz if the change in its output is bounded by the change in its input: \[ |f(x_1) - f(x_2)| \leq \|x_1 - x_2\|. \] Intuitively, this imposes a global “speed limit” on the critic: small changes in the image should not cause arbitrarily large changes in the critic score. When \(f\) is differentiable almost everywhere, 1-Lipschitzness implies \[ \|\nabla _x f(x)\|_2 \leq 1 \quad \mbox{for almost every } x \in \mathcal {X}, \] and (under mild regularity conditions) the converse holds as well. See Villani [646] for a rigorous treatment of Lipschitz continuity in optimal transport.
The WGAN-GP Loss Function WGAN-GP enforces this constraint softly via regularization. We train the critic to minimize \[ \mathcal {L}_{\mbox{critic}}^{\mbox{GP}} = \underbrace {\mathbb {E}_{\tilde {x} \sim p_G}[f(\tilde {x})] \;-\; \mathbb {E}_{x \sim p_{\mbox{data}}}[f(x)]}_{\mbox{WGAN critic loss (minimization form)}} \;+\; \lambda \; \underbrace {\mathbb {E}_{\hat {x} \sim p_{\hat {x}}} \left [ \left (\|\nabla _{\hat {x}} f(\hat {x})\|_2 - 1\right )^2 \right ]}_{\mbox{gradient penalty}}. \] The generator is updated using the standard WGAN objective: \[ \mathcal {L}_{G} = -\mathbb {E}_{z \sim p(z)}\bigl [f(G(z))\bigr ]. \] Here \( \lambda \) is a regularization coefficient (typically \( \lambda = 10 \)). The distribution \(p_{\hat {x}}\) is defined by the interpolated samples used to evaluate the penalty, described next.
Interpolated Points: Enforcing a “Controlled Slope” Where It Matters Enforcing \(\|\nabla f\|\le 1\) everywhere in high-dimensional space is both intractable and unnecessary. WGAN-GP instead enforces a controlled slope in the region that most strongly influences learning: the “bridge” between current generated samples and real samples.
- The bridge intuition (local changes should cause local score changes): The generator updates its parameters by backpropagating through the critic score \(f(G(z))\). Consequently, the geometry of \(f\) in the neighborhood of generated samples—and in the nearby region leading toward real samples—determines the direction and stability of the generator’s gradient. If \(f\) becomes too steep in this region, generator updates can become unstable; if \(f\) becomes too flat, learning stalls.
- Implementation via interpolation (sampling the bridge): WGAN-GP approximates this bridge by sampling straight-line segments between random real and fake pairs. Given \(x \sim p_{\mbox{data}}\), \(\tilde {x} \sim p_G\), and \(\varepsilon \sim \mathcal {U}[0,1]\), define \[ \hat {x} \;=\; \varepsilon \,x \;+\; (1-\varepsilon )\,\tilde {x}. \] The distribution \(p_{\hat {x}}\) is the law of \(\hat {x}\) induced by this sampling procedure. The penalty is evaluated on these \(\hat {x}\), encouraging the critic to behave like a well-conditioned “ramp” between real and fake.
- An infinitesimal-change view (Explicit Intuition): For a small perturbation \(\delta \), a first-order approximation gives \[ |f(\hat {x}+\delta ) - f(\hat {x})| \;\approx \; |\langle \nabla _{\hat {x}} f(\hat {x}), \delta \rangle | \;\le \; \|\nabla _{\hat {x}} f(\hat {x})\|_2 \,\|\delta \|_2. \] Thus, penalizing deviations of \(\|\nabla _{\hat {x}} f(\hat {x})\|_2\) from 1 explicitly enforces a controlled sensitivity: it ensures that changing the image slightly along this bridge changes the critic score by a predictable, bounded amount (roughly proportional to the change in the image).
Why Penalize Toward Norm \(1\) (Not Just “\(\le 1\)”)? Formally, the Kantorovich–Rubinstein dual requires \(\|\nabla f\|\le 1\). WGAN-GP uses the two-sided penalty \((\|\nabla f\|_2 - 1)^2\) as a practical way to produce a critic that is both Lipschitz-compliant and useful for learning.
- Upper bound (preventing instability): Enforcing gradients near \(1\) automatically discourages \(\|\nabla f\|\gg 1\), which would make the critic hypersensitive. This prevents the exploding gradients that often destabilize standard GANs.
- Avoiding flat regions (ensuring signal): If the critic becomes flat on the bridge (\(\|\nabla f\|\approx 0\)), then \(f\) changes little as \(\tilde {x}\) moves toward \(x\). In this scenario, the generator receives a zero or negligible gradient and stops learning. The two-sided penalty discourages such degeneracy by encouraging a non-trivial slope on the bridge.
-
A simple 1D example (Flat vs. Steep vs. Controlled): Consider a scalar input \(t \in [0,1]\) parameterizing a path from fake (\(t=0\)) to real (\(t=1\)), and let the critic along this path be \(f(t)\).
- Flat (\(f'(t) \approx 0\)): The critic outputs constant scores. The generator gets no signal.
- Steep (\(f'(t) \gg 1\)): The critic jumps rapidly. Generator updates are unstable and explode.
- Controlled (\(f'(t) \approx 1\)): The critic acts like a ramp. Moving \(t\) from 0 to 1 improves the score steadily. This provides the ideal, constant-magnitude learning signal.
Comparison: Standard GANs vs. Clipped WGAN vs. WGAN-GP
- 1.
- Vs. Standard GANs: Standard GANs optimize a classification objective with a sigmoid output. When the discriminator is perfect, the sigmoid saturates, and gradients vanish. WGAN-GP uses a linear critic with a gradient penalty; this combination prevents saturation and guarantees a steady flow of gradients even when the critic is accurate.
- 2.
- Vs. WGAN with Weight Clipping: Weight clipping constrains the critic’s parameters to a box, which biases the network toward simple, linear functions and limits its capacity. In contrast, WGAN-GP constrains the local slope of the function. This allows the parameters themselves to be large, enabling the critic to learn complex, non-linear decision boundaries (e.g., deep ResNets) while maintaining stability.
Why This Avoids Over-Regularization Because the penalty is applied only on the interpolated bridge samples \(\hat {x}\), the critic is not forced to satisfy a tight constraint everywhere in the vast input space \(\mathcal {X}\). Instead, it is encouraged to be well-behaved precisely in the region that dominates generator learning dynamics, yielding a practical compromise: controlled sensitivity where it matters, without globally crippling the critic’s capacity.
Code Walkthrough: Penalty Computation Below is a robust PyTorch implementation of the gradient penalty. Note the use of create_graph=True, which is essential because the penalty depends on \(\nabla _{\hat {x}} f(\hat {x})\); updating the critic therefore requires differentiating through this gradient computation.
def compute_gradient_penalty(critic, real_samples, fake_samples, device):
"""
WGAN-GP gradient penalty: E[(||grad_xhat f(xhat)||_2 - 1)^2].
Assumes fake_samples are treated as constants during the critic update.
"""
# Detach fake samples to avoid backprop to G during critic update
fake_samples = fake_samples.detach()
# 1) Sample interpolation coefficients and build x_hat
alpha = torch.rand(real_samples.size(0), 1, 1, 1, device=device)
alpha = alpha.expand_as(real_samples)
x_hat = (alpha * real_samples + (1 - alpha) * fake_samples).requires_grad_(True)
# 2) Critic output on interpolates
f_hat = critic(x_hat)
# 3) Compute grad_{x_hat} f(x_hat)
grad_outputs = torch.ones_like(f_hat)
gradients = torch.autograd.grad(
outputs=f_hat,
inputs=x_hat,
grad_outputs=grad_outputs,
create_graph=True, # enables backprop through the gradient norm
retain_graph=True
)[0]
# 4) Per-sample L2 norm and penalty
gradients = gradients.view(gradients.size(0), -1)
grad_norm = gradients.norm(2, dim=1)
return ((grad_norm - 1) ** 2).mean()Step-by-step intuition:
- (a)
- Sample & interpolate: Mix real and fake samples to form \(x_{\hat {}}\), and set requires_grad_(True) so gradients w.r.t. inputs are tracked.
- (b)
- Differentiate through the critic: Use torch.autograd.grad to compute \(\nabla _{x_{\hat {}}} f(x_{\hat {}})\). Setting create_graph=True is crucial so the penalty can backpropagate into critic parameters.
- (c)
- Apply the penalty: Flatten per sample, compute \(\ell _2\) norms, and penalize \(\bigl (\| \nabla _{x_{\hat {}}} f(x_{\hat {}})\|_2 - 1\bigr )^2\).
Resulting Dynamics & Why It Helps
- Stabilized training: The critic avoids the pathological saturation or massive weight expansions that occur with naive clipping. Its gradients remain “under control” precisely in the real-fake frontier.
- More reliable gradients in practice: Compared to clipped WGANs, the critic is less likely to become overly flat or excessively steep near the real–fake frontier, which often yields a smoother and more informative learning signal for the generator.
- Minimal overhead, maximum benefits: The penalty is computed via a simple first-order differentiation step. Empirically, it yields a more robust Lipschitz enforcement than globally constraining network weights.
Interpreting the Loss Components
- The Wasserstein Estimate: \[ \mathbb {E}[f(\tilde {x})] - \mathbb {E}[f(x)] \] The critic minimizes \(\mathbb {E}_{\tilde {x}}[f(\tilde {x})] - \mathbb {E}_{x}[f(x)]\), which is equivalent to maximizing \(\mathbb {E}_{x}[f(x)] - \mathbb {E}_{\tilde {x}}[f(\tilde {x})]\), thereby widening the real–fake score gap.
- The Gradient Penalty: \[ \lambda \, \mathbb {E} \left [\left ( \|\nabla _{\hat {x}} f(\hat {x})\|_2 - 1 \right )^2\right ] \] Why penalize deviation from 1, rather than just values \(>1\)? To maximize the Wasserstein gap, the optimal critic tends to use as much slope as allowed (up to the Lipschitz limit) in regions that separate real from generated samples. Penalizing deviation from \(1\) encourages non-degenerate slopes (so infinitesimal changes in \(\hat {x}\) produce informative but bounded changes in \(f(\hat {x})\)) while still controlling excessive gradients.
Key Benefits of the Gradient Penalty vs. Weight Clipping
- Precisely targeted constraint: By checking gradients only on line segments connecting real and generated data, WGAN-GP avoids excessive regularization in unimportant regions.
- Avoids clipping pathologies: Hard-clipping forces weights into a small box, often causing the critic to behave like a simple linear function. The soft gradient penalty allows for complex, non-linear critics.
- Supports deeper architectures: WGAN-GP is compatible with deep ResNets without suffering the instabilities or gradient vanishing often observed in clipped WGANs.
Practical Implementation Note: Avoid Batch Normalization A critical requirement for WGAN-GP is that the critic must not use Batch Normalization. The gradient penalty is computed w.r.t. individual inputs. BatchNorm couples samples in a batch, invalidating the independence assumption of the penalty. Use Layer Normalization, Instance Normalization, or no normalization in the critic (BatchNorm may still be used in the generator, since the gradient penalty is not taken w.r.t. generator inputs).
Architectural Robustness One of the most compelling benefits of WGAN-GP is its architectural flexibility. It works reliably with MLPs, DCGANs, and deep ResNets—even when using the same hyperparameters across models.
State-of-the-Art Results on CIFAR-10 (At the Time of Publication) In the experimental setup of Gulrajani et al. [194], WGAN-GP with a ResNet-based critic achieves leading Inception scores on CIFAR-10 among the compared unsupervised baselines at the time of publication. Since then, many subsequent GAN variants and training schemes have surpassed these numbers; here, the table is best read as evidence that stable Lipschitz enforcement enables higher-capacity architectures to train reliably and reach strong results under a fixed, controlled comparison.
| Unsupervised Model | Inception Score |
|---|---|
| ALI (Dumoulin et al.) | 5.34 \(\pm \) 0.05 |
| DCGAN (Radford et al.) | 6.16 \(\pm \) 0.07 |
| Improved GAN (Salimans et al.) | 6.86 \(\pm \) 0.06 |
| EGAN-Ent-VI | 7.07 \(\pm \) 0.10 |
| DFM | 7.72 \(\pm \) 0.13 |
| WGAN-GP (ResNet) | 7.86 \(\pm \) 0.07 |
Conclusion WGAN-GP combines the theoretical strength of optimal transport with the practical stability of smooth gradient regularization. It replaces rigid weight clipping with a principled, differentiable loss term—enabling deeper architectures, smoother convergence, and high-quality generation across domains. Its success laid the groundwork for many subsequent GAN improvements, including conditional models and progressive training techniques.
Enrichment 20.6: The StyleGAN Family
The StyleGAN family, developed by Karras et al. [278, 280, 279], represents a major advancement in generative modeling. These architectures build upon the foundational Progressive Growing of GANs (ProGAN) [281], introducing a radically different generator design that enables better disentanglement, fine-grained control, and superior image quality.
Enrichment 20.6.1: ProGAN Overview: A Stability-Oriented Design
ProGAN [281] stabilizes GAN training by progressively growing both the generator and discriminator during optimization. Instead of learning to synthesize \(1024\times 1024\) images from the start, training begins at a very low spatial resolution (typically \(4\times 4\)) and then doubles resolution in stages: \[ 4^2 \rightarrow 8^2 \rightarrow 16^2 \rightarrow \cdots \rightarrow 1024^2. \] The core idea is that early stages learn global structure (pose, layout, coarse shape) in a low-dimensional pixel space, while later stages specialize in high-frequency detail (texture, strands of hair, wrinkles), reducing optimization shock and improving stability.
Training Strategy ProGAN couples a resolution-aware curriculum with several stabilization heuristics (pixelwise feature normalization, minibatch standard deviation, equalized learning rate). The progressive schedule has two intertwined components: (i) architectural expansion and (ii) a fade-in transition that smoothly introduces newly added layers.
-
Progressive layer expansion (the core mechanism): To move from resolution \(R\) to \(2R\), ProGAN does not restart training from scratch. Instead, it grows both networks by appending a small, highest-resolution block while reusing the previously trained lower-resolution networks unchanged as an Old Stack. Conceptually, the Old Stack has already learned how to model and judge coarse structure at resolution \(R\), so the newly added parameters can concentrate on the incremental difficulty of handling finer-scale detail that only exists at resolution \(2R\). This isolates the new learning problem, reduces optimization shock, and makes the adversarial game substantially better conditioned.
-
Generator growth (adding detail at \(2R\)): Let \(G_R\) denote the generator after training at resolution \(R\). When run up to its last internal feature tensor, it produces \(h_R \in \mathbb {R}^{R \times R \times C}\), which encodes a stable coarse scene description (global pose, layout, low-frequency shape). To reach \(2R\), ProGAN upsamples this feature map and appends a New Block (typically two \(3\times 3\) convolutions) that operates specifically at the new resolution. Finally, a new toRGB head (a \(1\times 1\) convolution) projects the refined features to the three RGB channels: \[ \underbrace {z \to \cdots \to h_R}_{\substack {\mbox{Old Stack} \\ (R \times R \times C)}} \;\xrightarrow {\;\mbox{upsample}\;} \mathbb {R}^{2R\times 2R\times C} \;\xrightarrow [\substack {\mbox{New Block} \\ \mbox{(learns fine detail)}}]{\mbox{Two } 3\times 3 \mbox{ Convs}} h_{2R} \in \mathbb {R}^{2R\times 2R\times C'} \;\xrightarrow [\mathbf {1\times 1}]{\texttt{toRGB}} \underbrace {x_{2R}}_{\substack {\mbox{Output Image} \\ (2R \times 2R \times 3)}}. \] In practice, upsampling is performed via nearest-neighbor interpolation (to avoid checkerboard artifacts from transposed convolutions), followed by the two \(3\times 3\) convolutions.
The New Block and its toRGB head are the only components that must learn how to express and render the additional degrees of freedom available at \(2R\) (sharper edges, higher-frequency texture statistics), while the Old Stack continues to provide the already-learned global structure. This division of labor is the main reason progressive growing is easier to optimize than training a full \(2R\)-resolution generator from scratch, where global geometry and micro-texture would need to be discovered simultaneously under a rapidly strengthening discriminator.
-
Discriminator growth (mirroring the generator at \(2R\)): Let \(D_R\) denote the discriminator trained at resolution \(R\). At this point in training, \(D_R\) is already a competent “coarse realism” judge: it has learned to map an \(R\times R\) image (or, equivalently, an \(R\times R\) feature representation) to a scalar score by detecting global inconsistencies such as wrong layout, implausible shapes, or broken low-frequency statistics.
When we increase the generator’s output resolution to \(2R\), the discriminator must expand its perceptual bandwidth: it should still leverage its learned global judgment, but it must also become sensitive to the new high-frequency evidence that now exists in \(2R\times 2R\) images (e.g., sharper edges, texture regularities, aliasing artifacts). ProGAN achieves this without discarding the already-trained discriminator by growing the discriminator in the opposite direction of the generator: it prepends a small, high-resolution processing block at the input side, and then plugs the pre-trained \(D_R\) (the Old Stack) in after this new block.
Concretely, the new input-side block consists of a fromRGB stem (a \(1\times 1\) convolution) that lifts raw pixels into feature space, followed by two \(3\times 3\) convolutions that operate at resolution \(2R\) to analyze fine-detail cues, and finally an average-pooling downsample that produces an \(R\times R\) feature tensor of the shape expected by the old discriminator stack: \[ \underbrace {x_{2R}}_{\substack {\mbox{Input Image} \\ (2R \times 2R \times 3)}} \;\xrightarrow [\mathbf {1\times 1}]{\texttt{fromRGB}} \underbrace {\mathbb {R}^{2R\times 2R\times C'}}_{\substack {\mbox{High-res features} \\ \mbox{(new stem output)}}} \;\xrightarrow [\substack {\mbox{New Block} \\ \mbox{(critiques fine detail)}}]{\mbox{Two } 3\times 3 \mbox{ Convs}} \mathbb {R}^{2R\times 2R\times C} \;\xrightarrow {\;\mbox{avgpool}\;} \underbrace {\mathbb {R}^{R\times R\times C}}_{\substack {\mbox{Compatible input for} \\ \mbox{Old Stack } D_R}} \;\xrightarrow {\;D_R\;} \mbox{Score}. \]
This construction makes the training dynamics much better behaved. The old discriminator \(D_R\) is not “thrown away” and relearned; it remains intact and continues to process an \(R\times R\) representation with the same tensor shape and comparable semantic level as in the previous stage. In other words, the newly added high-resolution block acts as a learned front-end sensor: it observes the extra information available at \(2R\), extracts the fine-scale evidence that was previously invisible, and then hands a downsampled summary to the already-trained “global judge” \(D_R\).
As a result, the discriminator becomes stronger exactly where the generator gained new degrees of freedom, but it does so in a controlled, localized way: most of the discriminator’s capability (the Old Stack) remains a stable foundation for judging geometry and low-frequency structure, while only the new input-side block must learn how to interpret and penalize higher-frequency artifacts. This is one of the key reasons progressive growing improves stability compared to training a large \(2R\)-resolution discriminator from scratch, which can either (i) rapidly overpower the generator before it has learned coarse structure, or (ii) destabilize optimization by forcing the entire discriminator to simultaneously learn both global and fine-scale judgments from an initially weak generator distribution.
-
-
Fade-in mechanism (what is blended, when, and how it is controlled): Abruptly inserting new layers can destabilize training, because the discriminator suddenly receives higher-resolution inputs and the generator suddenly produces outputs through untrained weights. ProGAN avoids this by linearly blending two image pathways during a dedicated transition period.
At resolution \(2R\), the generator produces the final RGB image via: \[ x^{\mbox{out}}_{2R}(\alpha ) = \alpha \cdot x^{\mbox{high}}_{2R} + (1-\alpha )\cdot x^{\mbox{low}}_{2R}, \qquad \alpha \in [0,1], \] where:
- \(x^{\mbox{high}}_{2R}\) is the RGB output from the new block (upsample \(\rightarrow \) conv \(\rightarrow \) toRGB) at resolution \(2R\).
- \(x^{\mbox{low}}_{2R}\) is obtained by taking the previous stage output \(x_R \in \mathbb {R}^{R\times R\times 3}\) and upsampling it to \(2R\times 2R\) (using the same deterministic upsampling).
The discriminator uses a matching fade-in at its input: \[ \phi ^{\mbox{in}}_{2R}(\alpha ) = \alpha \cdot \phi ^{\mbox{high}}_{2R} + (1-\alpha )\cdot \phi ^{\mbox{low}}_{2R}, \] where \(\phi ^{\mbox{high}}_{2R}\) is the feature map after the new fromRGB and convs at \(2R\), and \(\phi ^{\mbox{low}}_{2R}\) is obtained by downsampling the input image to \(R\times R\) and passing it through the previous-stage fromRGB branch.
How \(\alpha \) is scheduled in practice: \(\alpha \) is treated as a deterministic scalar that is updated as training progresses, typically linearly with the number of images processed during the fade-in phase: \[ \alpha \leftarrow \min \!\left (1,\; \frac {n}{N_{\mbox{fade}}}\right ), \] where \(n\) is the number of training images seen so far in the fade-in phase and \(N_{\mbox{fade}}\) is a fixed hyperparameter (often specified in “kimg”). Equivalently, in code one updates \(\alpha \) once per minibatch using the minibatch size. After the fade-in phase completes (\(\alpha =1\)), ProGAN continues training at the new resolution for an additional stabilization phase with \(\alpha \) fixed to 1.
-
Stage completion criterion (schedule, not adaptive metrics): ProGAN uses a fixed curriculum, not an adaptive convergence test. Each resolution stage consists of:
- Fade-in phase: linearly ramp \(\alpha :0\rightarrow 1\) over \(N_{\mbox{fade}}\) images.
- Stabilization phase: continue training for \(N_{\mbox{stab}}\) images with \(\alpha =1\).
The values \(N_{\mbox{fade}},N_{\mbox{stab}}\) are resolution-dependent hyperparameters (often larger for high resolutions; e.g., hundreds of thousands of images per phase at \(128^2\) and above in the original setup).
- Upsampling and downsampling operators (why these choices): The generator uses nearest-neighbor upsampling followed by \(3\times 3\) convolutions to avoid the checkerboard artifacts often associated with transposed convolutions. The discriminator uses average pooling for downsampling to provide a simple, stable low-pass behavior, again followed by \(3\times 3\) convolutions.
Why This Works Progressive growing decomposes a difficult high-resolution game into a sequence of easier games:
- Large-scale structure first: At \(4^2\) or \(8^2\), the networks learn global layout with very limited degrees of freedom, reducing the chance that training collapses into high-frequency “noise wars” between generator and discriminator.
- Detail refinement later: Each new block primarily controls a narrower frequency band (finer scales), so it can specialize in textures while earlier blocks preserve global semantics.
- Compute efficiency: Early stages are much cheaper, and a substantial portion of training time occurs before reaching the largest resolutions, reducing total compute versus training exclusively at full resolution.
Stabilization Heuristics Beyond the progressive growth curriculum, ProGAN introduces three concrete modifications whose shared goal is to make the generator–discriminator game numerically well-conditioned: (i) keep generator signal magnitudes from drifting or “escalating” across depth and time, (ii) give the discriminator an explicit handle on within-batch diversity so collapse is easier to detect, and (iii) equalize the effective step sizes of different layers by a simple re-parameterization of convolution weights.
-
Pixelwise feature normalization (PixelNorm in the generator): ProGAN inserts a deterministic normalization step after each convolutional layer in the generator (in the original architecture, after the nonlinearity), applied independently at every spatial location and independently for every sample in the minibatch. Let \(a_{h,w} \in \mathbb {R}^{C}\) denote the channel vector at pixel \((h,w)\) in some intermediate generator feature map (for a fixed sample). PixelNorm rescales this vector by its root-mean-square (RMS) magnitude: \[ b_{h,w} = \frac {a_{h,w}}{\sqrt {\frac {1}{C}\sum _{j=1}^{C}\bigl (a_{h,w}^{(j)}\bigr )^2 + \epsilon }}, \qquad b_{h,w}\in \mathbb {R}^{C}. \] This operation has no batch dependence and no learnable affine parameters (no \(\gamma ,\beta \)); it is a pure, local rescaling.
Why this particular form helps. The generator repeatedly upsamples and refines features, so small imbalances in per-layer gain can amplify over depth, leading to layers that operate at very different dynamic ranges. PixelNorm acts as a per-location “automatic gain control”: it keeps the feature energy at each pixel close to a fixed scale, while still allowing the network to encode semantics in the direction of \(a_{h,w}\) (i.e., relative patterns across channels). This tends to reduce sensitivity to initialization and learning-rate choices, and it limits runaway signal magnitudes without forcing the generator to be linear or low-capacity.
How it differs from common normalizers. BatchNorm normalizes using minibatch statistics, coupling unrelated samples and potentially injecting batch-dependent artifacts into generation; PixelNorm avoids this entirely by operating per sample and per spatial location. LayerNorm typically uses both centering and scaling (subtracting a mean and dividing by a standard deviation over channels, sometimes over larger axes depending on implementation) and is usually paired with a learnable affine transform; PixelNorm performs only RMS-based rescaling (no mean subtraction) and no learned gain/shift, which preserves sparsity patterns induced by ReLU/leaky-ReLU and keeps the normalization as a lightweight stabilizer rather than a feature-wise affine re-mapping. In the ProGAN context, the intent is not “feature whitening” but simply keeping the generator’s internal signal scale under control throughout progressive growth.
-
Minibatch standard deviation (explicit diversity signal in the discriminator): Mode collapse is difficult for a standard discriminator to detect because it scores each image independently: if the generator outputs the same plausible-looking image for many latent codes, per-sample classification can remain ambiguous even though the set of samples is clearly non-diverse. ProGAN addresses this by appending a statistic that measures variation across the minibatch to the discriminator’s activations near the end of the network.
Computation. Let \(f \in \mathbb {R}^{N\times C\times H\times W}\) be a discriminator feature tensor for a minibatch of size \(N\) at some late layer (typically when spatial resolution is already small).
The minibatch standard deviation layer computes:
- (a)
- Batch-wise deviation: compute the per-feature, per-location standard deviation across the minibatch, \[ \sigma _{c,h,w} = \sqrt {\frac {1}{N}\sum _{n=1}^{N}\bigl (f_{n,c,h,w}-\mu _{c,h,w}\bigr )^2 + \epsilon }, \qquad \mu _{c,h,w}=\frac {1}{N}\sum _{n=1}^{N} f_{n,c,h,w}. \]
- (b)
- Aggregate to a scalar: average \(\sigma _{c,h,w}\) over channels and spatial positions to obtain a single scalar \(s\in \mathbb {R}\), \[ s = \frac {1}{CHW}\sum _{c,h,w}\sigma _{c,h,w}. \]
- (c)
- Broadcast and concatenate: replicate \(s\) to a constant feature map \(s\mathbf {1}\in \mathbb {R}^{N\times 1\times H\times W}\) and concatenate it as an additional channel: \[ f' = \mathrm {Concat}\bigl (f,\; s\mathbf {1}\bigr )\in \mathbb {R}^{N\times (C+1)\times H\times W}. \] How it is used inside the discriminator: the next discriminator layers simply continue operating on \(f'\) (now with \(C+1\) channels). In particular, the subsequent convolution (or final dense layers, depending on the stage) has trainable weights on this extra channel, so it can treat \(s\mathbf {1}\) as a dedicated “diversity sensor” and incorporate it into the real/fake decision alongside the usual learned features.
Why this discourages collapse. If the generator collapses so that samples in the batch become nearly identical, then many discriminator features also become nearly identical across \(n\), driving \(\sigma _{c,h,w}\) (and hence \(s\)) toward zero. The discriminator can then learn a simple rule: “real batches tend to exhibit non-trivial variation, whereas collapsed fake batches do not”. This converts lack of diversity into an easily separable cue, forcing the generator to maintain perceptible sample-to-sample variability in order to keep the discriminator uncertain. The aggregation to a single scalar is deliberate: it provides a robust, low-variance signal that is hard to game by injecting diversity into only a small subset of channels or spatial positions.
How this affects the generator (the feedback loop). Although \(s\) is computed inside the discriminator, it changes the generator’s training signal because the discriminator’s output now depends on a quantity that summarizes between-sample variation. During backpropagation, gradients flow from the discriminator score through the weights that read the extra channel \(s\mathbf {1}\), then through the computation of \(s\), and finally back to the generator parameters via the generated samples that contributed to \(f\). Consequently, if the discriminator learns to penalize low \(s\) as “fake”, the generator can only improve its objective by producing batches for which the discriminator features are not nearly identical across different latent codes. Operationally, this introduces a pressure to map different \(z\) values to meaningfully different outputs (and intermediate discriminator activations), counteracting the collapsed solution in which \(G(z_1)\approx G(z_2)\) for many \(z_1\neq z_2\).
-
Equalized learning rate (EqLR): Standard initializations (like He or Xavier) scale weights once at initialization to ensure stable signal magnitudes. However, this creates a side effect: layers with different fan-ins end up with weights of vastly different magnitudes (e.g., \(0.01\) vs \(1.0\)). Since modern optimizers (like Adam) often use a global learning rate, this leads to update speeds that vary wildly across layers. ProGAN solves this by decoupling the parameter scale from the signal scale.
The Mechanism (Runtime Scaling). First, recall that fan-in (\(n\)) is the number of input connections to a neuron (e.g., \(k^2 \cdot C_{in}\) for a convolution). In EqLR, we initialize all stored parameters \(w\) from a standard normal distribution \(\mathcal {N}(0, 1)\). Then, during every forward pass, we scale them dynamically: \[ w_{\mbox{effective}} = w \cdot c, \qquad \mbox{where } c = \sqrt {\frac {2}{n}}. \] The layer uses \(w_{\mbox{effective}}\) for convolution, ensuring the output activations have unit variance (just like He initialization).
Why this stabilizes training (The ”Learning Speed” Intuition). The benefit appears during the backward pass. To see why, compare a large layer (where weights must be small) under both schemes:
- Standard He Initialization: We initialize \(w \approx 0.01\). If the learning rate is \(\eta = 0.01\), a single gradient step can change the weight from \(0.01 \to 0.02\). This is a huge 100% relative change, causing the layer to train explosively fast and potentially diverge.
- EqLR: We initialize \(w \approx 1.0\). The constant \(c \approx 0.01\) handles the scaling downstream. Now, the same gradient update \(\eta = 0.01\) changes the stored parameter from \(1.0 \to 1.01\). This is a stable 1% relative change.
Result: By keeping all stored parameters in the same range (\(w \sim 1\)), EqLR ensures that all layers—regardless of their size—learn at the same relative speed. This prevents the ”race condition” where some layers adapt instantly while others lag behind, which is critical for the delicate balance of GAN training.
Note on Inference: There is no train–test discrepancy. The scaling \(c\) is a fixed mathematical constant derived from the architecture dimensions. It is applied identically during training and inference.
Enrichment 20.6.1.1: Limitations of ProGAN: Toward Style-Based Generators
While ProGAN successfully synthesized high-resolution images with impressive quality, its architecture introduced three fundamental limitations that StyleGAN sought to overcome:
- Latent code bottleneck: The latent vector \( z \sim \mathcal {N}(0, I) \) is injected only once at the input. Its influence can weaken in deeper layers, which are responsible for fine-grained texture and microstructure.
- Entangled representations: High-level attributes such as pose, identity, and background are mixed in the latent space, so small perturbations in \( z \) can produce unpredictable coupled changes across multiple factors.
- Lack of stochastic control: Fine-scale stochastic details (e.g., pores, hair microstructure, subtle lighting variation) are not explicitly controlled or reproducibly isolatable in the generator.
These limitations motivated a rethinking of the generator design—leading to StyleGAN, which introduces multi-resolution modulation, explicit stochastic inputs, and a non-linear mapping from \( z \) to intermediate style vectors to improve disentanglement and controllability.
Enrichment 20.6.2: StyleGAN: Style-Based Synthesis via Latent Modulation
While ProGAN succeeded in generating high-resolution images by progressively growing both the generator and discriminator, its architecture left a core limitation unresolved: the latent code \( z \sim \mathcal {N}(0, I) \) was injected only at the input layer of the generator. As a result, deeper layers — responsible for fine-grained details — received no direct influence from the latent space, making it difficult to control semantic factors in a disentangled or interpretable way.
StyleGAN, proposed by Karras et al. [278], addresses this by completely redesigning the generator, while keeping the ProGAN discriminator largely unchanged. The key idea is to inject the latent code — transformed into an intermediate vector \( w \in \mathcal {W} \) — into every layer of the generator. This turns the generator into a learned stack of stylization blocks, where each resolution is modulated independently by semantic information.
This architectural shift repositions the generator not as a direct decoder from latent to image, but as a controllable, hierarchical stylization process — enabling high-quality synthesis and fine-grained control over attributes like pose, texture, and color.
Key Architectural Ideas
(1) Mapping Network (\(\mathcal {Z} \to \mathcal {W}\)): Instead of injecting the latent vector \( z \in \mathbb {R}^d \) directly into the generator, StyleGAN introduces a learned mapping network — an 8-layer MLP that transforms \( z \) into an intermediate latent vector \( w = f(z) \in \mathcal {W} \). This design serves two main purposes:
- Alleviating entanglement (empirically): The original latent space \( \mathcal {Z} \) tends to entangle unrelated attributes — such as pose, hairstyle, and facial expression — making them difficult to control independently. The mapping network learns to reparameterize the latent space into \( \mathcal {W} \), which is observed (empirically) to be more disentangled: specific dimensions in \( w \) often correspond to localized and semantically meaningful variations.
- Improved editability: The intermediate latent space \( \mathcal {W} \) facilitates smoother interpolation and manipulation. Small movements in \( w \) tend to yield isolated, predictable image changes (e.g., adjusting skin tone or head orientation) without unintentionally affecting other factors.
Why Not Just Increase the Dimensionality of \( z \)? A natural question arises: could increasing the dimensionality of the original latent vector \( z \) achieve the same effect as using a mapping network? In practice, the answer is no — the limitation lies not in the capacity of \( z \), but in its geometry.
Latents drawn from \( \mathcal {N}(0, I) \) are distributed isotropically: all directions in \( \mathcal {Z} \) are equally likely, with no preference for meaningful directions of variation. This forces the generator to learn highly nonlinear transformations to decode useful structure from \( z \), often leading to entangled image features. Merely increasing the dimension expands the space without addressing this fundamental mismatch.
By contrast, the mapping network explicitly learns to warp \( \mathcal {Z} \) into \( \mathcal {W} \), organizing it such that different axes correspond more closely to semantically interpretable changes. While not theoretically guaranteed, this empirically observed disentanglement leads to significant improvements in image control, interpolation quality, and latent traversal. Karras et al. [278] demonstrate that using \( w \in \mathcal {W} \) consistently outperforms direct use of \( z \) — even with larger dimension — in terms of editability and semantic structure.
(2) Modulating Each Layer via AdaIN (Block A): In ProGAN, the latent code \(z\) is injected only once at the input. To prevent signal magnitude escalation, ProGAN uses PixelNorm, which forces every feature vector to unit norm. While stable, this is rigid: it applies the same normalization rule to every image, denying the latent code the ability to emphasize or suppress specific features sample-by-sample.
The Feature Statistics Hypothesis: What is “Style”? To understand StyleGAN’s solution, we must first define what “style” means in the context of Convolutional Neural Networks. Building on insights from neural style transfer [248], StyleGAN relies on the Feature Statistics Hypothesis:
- Spatial Layout (Content): The relative spatial locations of peaks and valleys in a feature map encode geometry (e.g., “an eye is at pixel \((10,10)\)”).
- Global Statistics (Style): The channel-wise mean and variance encode the texture or appearance (e.g., “how strong are the edges globally?” or “what is the background lighting?”).
Under this hypothesis, we can alter the “style” of an image simply by overwriting its feature map statistics, without needing to modify the spatial layout directly.
The “Wash and Paint” Mechanism (AdaIN). StyleGAN replaces PixelNorm with Adaptive Instance Normalization (AdaIN), turning each synthesis layer into a latent-controlled feature-styling module.
Unlike neural style transfer, which borrows statistics from a reference image, StyleGAN predicts the target statistics from the intermediate latent code \(w\). The operation proceeds in two steps:
Step 1: The Wash (Instance Normalization). First, we strip the input features of their current style statistics. Let \(x_\ell \in \mathbb {R}^{N \times C_\ell \times H_\ell \times W_\ell }\) be the activation tensor at layer \(\ell \). For each sample \(i\) and channel \(c\), we compute the spatial mean \(\mu \) and standard deviation \(\sigma \) across the dimensions \((H_\ell , W_\ell )\): \[ \mbox{Norm}(x_{\ell ,i,c}) = \frac {x_{\ell ,i,c} - \mu _{\ell ,i,c}}{\sigma _{\ell ,i,c}}. \] This “wash” removes the global energy and offset from the feature map while preserving its relative spatial structure. Ideally, the network retains where the features are (the layout), but forgets how strong they are.
Step 2: The Paint (Latent-Driven Modulation). Next, StyleGAN “paints” new statistics onto this canonical canvas. The latent \(w\) is projected via a learned affine transform \(A_\ell \) into style parameters: \[ (\gamma _\ell (w), \beta _\ell (w)) = A_\ell (w), \quad \gamma _\ell , \beta _\ell \in \mathbb {R}^{C_\ell }. \] These parameters are broadcast across the spatial dimensions \((H_\ell , W_\ell )\) to modulate the normalized features: \[ \mathrm {AdaIN}(x_\ell , w) = \underbrace {\gamma _\ell (w)}_{\mbox{Scale}} \odot \mbox{Norm}(x_\ell ) + \underbrace {\beta _\ell (w)}_{\mbox{Bias}}. \]
Why does this work? (Mathematical Derivation). We can prove that this operation forces the output features to have exactly the statistics dictated by \(w\). Let \(\hat {x} = \mbox{Norm}(x)\). By construction, its spatial mean is 0 and variance is 1. The statistics of the output \(y = \gamma \hat {x} + \beta \) are: \[ \mathbb {E}[y] = \mathbb {E}[\gamma \hat {x} + \beta ] = \gamma \mathbb {E}[\hat {x}] + \beta = \beta , \] \[ \sqrt {\mbox{Var}[y]} = \sqrt {\mbox{Var}[\gamma \hat {x} + \beta ]} = \sqrt {\gamma ^2 \mbox{Var}[\hat {x}]} = \gamma . \] Thus, for every layer \(\ell \), the pair \((\beta _\ell (w), \gamma _\ell (w))\) is precisely the layer’s “style”: it directly dictates the baseline and contrast of every feature channel.
Intuition: The “Global Control Panel” Analogy. Imagine each channel \(c\) is a specific feature detector (e.g., Channel 42 detects “vertical wrinkles”). The AdaIN parameters act as a global control panel for these detectors:
-
Scale \(\gamma _{\ell ,c}\) (The Volume Knob): This controls the gain or contrast.
- High \(\gamma \): The volume is up. The detector’s response is amplified. Deep, sharp wrinkles appear wherever the layout indicates.
- Low \(\gamma \): The volume is down. The feature is muted or washed out.
-
Bias \(\beta _{\ell ,c}\) (The Offset Slider): This controls the baseline presence.
- High \(\beta \): The feature is active everywhere (e.g., brightening the global lighting condition).
- Low \(\beta \): The feature is suppressed below the activation threshold.
Key Limitations: Spatially Uniform and Channel-Wise Control. While powerful, the AdaIN mechanism imposes two strict algebraic constraints on how the latent code \(w\) can influence the image:
- Spatially Uniform Control: The parameters \(\gamma _\ell (w)\) and \(\beta _\ell (w)\) are scalars that are broadcast over all spatial locations \((H_\ell , W_\ell )\). This means \(w\) cannot directly specify “brighten the top-left corner” differently from the bottom-right. It can only modulate the entire feature detector globally. (Note: Localized effects like a glint can still be produced via the spatial layout of the input features \(x_\ell \), but \(w\) cannot selectively target them).
- Channel-Wise (Diagonal) Control: The modulation acts on each channel independently. The affine transformation scales and shifts individual feature detectors but cannot mix or rotate them based on the latent code. Any coordination between channels must be handled implicitly by the convolutional weights.
The Downside: Normalization Artifacts (“Droplets”). These limitations—specifically the Instance Normalization step (The “Wash”)—are the primary motivation for StyleGAN2. Because AdaIN re-normalizes every feature map to unit variance, it discards the relative signal strength between channels. To bypass this, the generator learns to create localized spikes in signal magnitude (blobs or “droplets”) in the background. These spikes inflate the variance \(\sigma \), allowing the generator to manipulate the normalization constant and effectively preserve signal magnitude elsewhere. StyleGAN2 resolves this by removing explicit normalization in favor of a new weight demodulation scheme, which preserves the benefits of style modulation without causing these artifacts.
Why this matters (Hierarchical Control): Despite the limitation, this mechanism yields the disentanglement properties StyleGAN is famous for:
- Explicit separation of layout and appearance: The spatial arrangement flows through the convolutions (the “content”), while \(w\) acts as an external controller that overwrites the statistics (the “style”).
- Sample-dependent behavior: The same convolutional filters behave differently for different images because their operating points are modulated by \(w\).
- Coarse-to-fine control: By modulating early layers, \(w\) controls the statistics of coarse features (pose, shape). By modulating deeper layers, it controls fine details (colors, micro-textures).
(3) Fixed Learned Input (Constant Tensor): A second innovation in StyleGAN is the use of a fixed learned input tensor: a constant trainable block of shape \( 4 \times 4 \times C \), shared across all samples. Unlike earlier GANs, where \( z \) or \( w \) was reshaped into an initial feature map, StyleGAN treats this constant as a base canvas.
All variation is introduced after this tensor, via style-based AdaIN modulation and additive noise. This decoupling is only viable because AdaIN provides a mechanism to inject sample-specific statistics into every layer. Without such modulation, a fixed input would collapse to identical outputs; with AdaIN, global structure emerges from the constant canvas, while semantic and stylistic variation is progressively layered in.
This design enforces:
- Consistent spatial structure: A shared input encourages stable layouts (e.g., facial geometry), while variations arise from modulation.
- Stronger disentanglement: Since \( w \) no longer defines spatial structure, it can focus on semantic and appearance attributes.
(4) Stochastic Detail Injection (Block B): To introduce variation in fine-grained details, StyleGAN adds Gaussian noise per spatial location. A single-channel noise map is drawn from \( \mathcal {N}(0,1) \), broadcast across channels, scaled by learned per-channel strengths, and added: \[ x' = x + \gamma \cdot \mbox{noise}, \qquad \gamma \in \mathbb {R}^C. \] This stochastic injection (Block B) allows natural variability (e.g., freckles, hair strands) without affecting global style.
Together, Blocks A and B mark a conceptual shift. Instead of mapping latent codes directly into images, StyleGAN decomposes generation into:
- Global, semantic variation: style-modulated via affine AdaIN.
- Local, stochastic variation: injected via per-layer noise.
Summary of changes from the original AdaIN: In Huang & Belongie’s work, AdaIN is a non-parametric alignment of statistics between two images [248]. StyleGAN modifies it into a parametric operator: style statistics are no longer extracted but predicted from latent codes. This repurposing enables a constant input tensor, because all per-sample variation is reintroduced through AdaIN and noise.
(5) Style Mixing Regularization: Breaking Co-Adaptation Across Layers A key goal of StyleGAN is to enable disentangled, scale-specific control over the synthesis process: early generator layers should influence coarse structure (e.g., face shape, pose), while later layers refine medium and fine details (e.g., eye color, skin texture). This structured control relies on the assumption that styles injected at each layer should work independently of one another.
However, if the generator always receives the same latent vector \( w \in \mathcal {W} \) at all layers during training, it may fall into a form of co-adaptation: early and late layers jointly specialize to particular combinations of attributes (e.g., blond hair only appears with pale skin), resulting in entangled features and reduced diversity.
Style Mixing Regularization disrupts this overfitting by occasionally injecting two distinct styles into the generator during training:
- Two latent codes \( z_1, z_2 \sim \mathcal {Z} \) are sampled and mapped to \( w_1 = f(z_1) \), \( w_2 = f(z_2) \).
- At a randomly chosen resolution boundary (e.g., \(16 \times 16\)), the generator applies \( w_1 \) to all earlier layers and switches to \( w_2 \) for the later layers.
Why this works: Because the generator is trained to synthesize coherent images even when style vectors abruptly change between layers, it cannot rely on tight correlations across resolutions. Instead, each layer must learn to independently interpret its style input. For example:
- If early layers specify a round face and neutral pose (from \( w_1 \)), then later layers must correctly render any eye shape, hair color, or lighting (from \( w_2 \)), regardless of what \( w_1 \) “would have” dictated.
- This prevents the network from implicitly coupling attributes (e.g., enforcing that a certain pose always goes with a certain hairstyle), which helps achieve true scale-specific disentanglement.
Result: Style Mixing acts as a form of regularization that:
- Improves editing robustness, as individual \( w \) vectors can be manipulated without unexpected side effects.
- Enables style transfer and recombination, where coarse features can be swapped independently of fine features.
- Encourages the generator to learn modularity, treating layer inputs as semantically independent rather than jointly entangled.
(6) Perceptual Path Length (PPL): Quantifying Disentanglement in Latent Space One of the defining features of a well-disentangled generative model is that interpolating between two latent codes should cause predictable, semantically smooth changes in the generated output. To formalize this idea, StyleGAN introduces the Perceptual Path Length (PPL) — a metric designed to measure the local smoothness of the generator’s mapping from latent codes to images.
PPL computes the perceptual distance between two very close interpolated latent codes in \( \mathcal {W} \)-space. Specifically, for two samples \( w_1, w_2 \sim \mathcal {W} \), we linearly interpolate between them and evaluate the visual difference between outputs at a small step: \[ \mbox{PPL} = \mathbb {E}_{w_1, w_2 \sim \mathcal {W}} \left [ \frac {1}{\epsilon ^2} \cdot \mathrm {LPIPS}(G(w(\epsilon )) , G(w(0))) \right ], \quad w(\epsilon ) = (1 - \epsilon ) w_1 + \epsilon w_2, \] where \( \epsilon \ll 1 \) (e.g., \( \epsilon = 10^{-4} \)) and \( G(w) \) is the image generated from \( w \).
What Is LPIPS? The Learned Perceptual Image Patch Similarity (LPIPS) metric [778] approximates human-perceived visual differences by comparing the feature activations of two images in a pretrained deep network (e.g., VGG-16). Unlike pixel-wise distances, LPIPS captures semantic similarity (e.g., facial expression, lighting) and is insensitive to small, perceptually irrelevant noise. This makes it especially suitable for assessing smoothness in generated outputs.
Why PPL Matters — and How It Relates to Training PPL serves two key roles:
- Evaluation: A low PPL score implies that the generator’s mapping is smooth — small steps in \( \mathcal {W} \) lead to controlled, localized changes in the image. High PPL values, in contrast, signal entanglement — for example, where a minor shift might simultaneously change pose and hairstyle.
- Regularization (StyleGAN2): StyleGAN2 adds a path length regularization term that encourages consistent image changes per unit movement in \( \mathcal {W} \). This is implemented by randomly perturbing latent codes and penalizing variance in the image-space response, pushing the generator toward more linear and disentangled behavior.
Crucially, PPL also helps diagnose the effectiveness of the generator’s latent modulation mechanisms, including AdaIN and noise injection. Improvements in PPL correlate with better interpretability and higher-quality style control. In this sense, PPL provides a complementary lens to adversarial loss functions — it doesn’t measure realism per se, but rather semantic coherence under manipulation.
(7) Loss Functions: From WGAN-GP to Non-Saturating GAN + R1 While StyleGAN’s architecture is central to its performance, stable training dynamics are equally crucial. To this end, the authors explored two major loss formulations across different experiments and datasets:
- WGAN-GP [194] — used for datasets like CelebA-HQ and LSUN, following the ProGAN pipeline. This loss minimizes the Wasserstein-1 distance while enforcing 1-Lipschitz continuity of the critic via a soft gradient penalty on interpolated samples.
- Non-Saturating GAN with R1 Regularization [424] — used in more recent experiments with the FFHQ dataset. This formulation applies a gradient penalty only to real samples, improving local stability and enabling deeper generators to converge reliably. To reduce computational overhead, the penalty is often applied lazily (e.g., every 16 steps).
These loss functions are not mutually exclusive with the perceptual evaluation tools like PPL. In fact, StyleGAN’s most robust results — especially in FFHQ — combine:
- 1.
- R1-regularized non-saturating loss for stable GAN convergence,
- 2.
- Path length regularization to encourage disentangled and smooth latent traversals (i.e., low PPL),
- 3.
- And LPIPS-based evaluation for empirical disentanglement measurement.
Together, these tools enable StyleGAN to not only generate photorealistic images, but also produce consistent, interpretable, and user-controllable latent manipulations — a key departure from earlier GANs where realism and control often conflicted.
Summary and Additional Contributions Beyond its architectural innovations — such as intermediate latent modulation, per-layer AdaIN, and stochastic noise injection — StyleGAN owes part of its success to the introduction of the Flickr-Faces-HQ (FFHQ) dataset. Compared to CelebA-HQ, FFHQ offers higher quality and broader diversity in age, ethnicity, accessories, and image backgrounds, enabling more robust and generalizable training.
This combination of structural disentanglement and dataset diversity allows StyleGAN to generate not only high-fidelity images, but also provides fine-grained control over semantic and local attributes. These advances collectively position StyleGAN as a foundational step toward interpretable and high-resolution image synthesis.
Emerging Capabilities
By separating global structure and local texture, StyleGAN enabled applications previously difficult in traditional GANs:
- Interpolation in latent space yields smooth, identity-preserving transitions.
- Truncation tricks can improve image quality by biasing \( w \) toward the center of \( \mathcal {W} \).
- Latent space editing tools can manipulate facial attributes with high precision.
This architectural shift — from latent vector injection to layer-wise modulation — laid the foundation for follow-up work on improved realism, artifact removal, and rigorous disentanglement.
Enrichment 20.6.3: StyleGAN2: Eliminating Artifacts, Improving Training Stability
StyleGAN2 [280] fundamentally refines the style-based generator framework, resolving key limitations of the original StyleGAN—most notably the so-called water droplet artifacts, excessive dependence on progressive growing, and training instabilities in high-resolution image synthesis. By removing or carefully restructuring problematic normalization modules, and by rethinking how noise and style manipulations are injected, StyleGAN2 achieves higher fidelity, improved consistency, and better disentanglement.
Enrichment 20.6.3.1: Background: From StyleGAN1 to StyleGAN2
StyleGAN1 (often termed StyleGAN1) introduced Adaptive Instance Normalization (AdaIN) in multiple generator layers, thereby allowing each feature map to be rescaled by learned style parameters. While this unlocked highly flexible style control and improved image quality, it also produced characteristic water droplet-like artifacts, most evident beyond \(64 \times 64\) resolution.
According to [280], the culprit lies in channel-wise normalization. AdaIN standardizes each feature map independently, removing not just its absolute magnitude but also any cross-channel correlations. In many cases, these correlations carry important relational information, such as spatial coherence or color harmony. By discarding them, the generator loses a mechanism to maintain consistent patterns across channels. In an effort to “sneak” crucial amplitude information forward, the network learns to insert extremely sharp, localized activation spikes. These spikes dominate the channel statistics at normalization time, effectively bypassing AdaIN’s constraints. Unfortunately, the localized spikes persist as structured distortions in the final images, creating the recognizable “droplet” effect.
To resolve these issues, StyleGAN2 reexamines the generator’s foundational design. Rather than normalizing activations via AdaIN, it shifts style control to a weight demodulation paradigm, ensuring that channel relationships remain intact. By scaling weights before convolution, the generator can preserve relative magnitudes across channels and avoid the need for spurious spikes.
Beyond demodulation, StyleGAN2 also relocates noise injection, removes progressive growing, and employs new regularization strategies, leading to improved stability and sharper image synthesis. We outline these core innovations below.
Enrichment 20.6.3.2: Weight Demodulation: A Principled Replacement for AdaIN
Context and Motivation: In the original StyleGAN (StyleGAN1), each layer applied Adaptive Instance Normalization (AdaIN) to the activations post-convolution, enforcing a learned mean and variance on each channel. This eroded cross-channel relationships and caused the network to insert “activation spikes” to reintroduce lost amplitude information, giving rise to “droplet” artifacts. StyleGAN2 addresses this by normalizing the weights instead of the activations, thereby preserving channel coherence and eliminating those artifacts.
High-Level Flow in a StyleGAN2 Generator Block:
- 1.
- Input Feature Map and Style Code. Each block receives:
- The input feature map from the preceding layer (or from a constant input if it is the first block).
- A latent code segment \(\mathbf {w}_\mathrm {latent}\) specific to that layer, from the block A. In practice, \(\mathbf {w}_\mathrm {latent}\) is generated by an affine transform applied to \(\mathbf {W}\) (the style vector shared across layers, typically after a learned mapping network).
- 2.
- Optional Upsampling (Skip Generator): Before passing the feature map into the convolution, StyleGAN2 may upsample the spatial resolution if this block operates at a higher resolution than the previous one. In the simplified “skip-generator” design, upsampling occurs right before the convolution in each block (rather than as a separate training phase, as in progressive growing).
- 3.
- Weight Modulation: \[ w_{ijk}^{\prime } \;=\; s_i \,\cdot \, w_{ijk}, \quad \mbox{where } s_i = \mathrm {affine}\bigl (\mathbf {w}_\mathrm {latent}\bigr )_i. \] The style vector \(\mathbf {w}_\mathrm {latent}\) is used to generate a set of scale factors \(\{s_i\}\). These factors modulate (i.e., rescale) the convolution’s filter weights by channel \(i\). As a result, each channel’s influence on the output can be boosted or suppressed depending on the style.
- 4.
- Weight Demodulation: \[ w_{ijk}^{\prime \prime } \;=\; \frac {w_{ijk}^{\prime }}{\sqrt {\sum _{i}\sum _{k} \bigl (w_{ijk}^{\prime }\bigr )^2 + \varepsilon }}. \] After modulation, each output channel \(j\) is normalized so that the final “modulated+demodulated” filter weights \(\{w_{ijk}^{\prime \prime }\}\) remain in a stable range. Crucially, this step does not standardize the activations channel-by-channel; it only ensures that the overall filter magnitudes do not explode or vanish.
- 5.
- Convolution: \[ \mathrm {output} \;=\; \mathrm {Conv}\bigl (\mathrm {input},\, w^{\prime \prime }\bigr ). \] The network now applies a standard 2D convolution using the newly modulated-and-demodulated weights \(w_{ijk}^{\prime \prime }\). The resulting activations reflect both the incoming feature map and the style-dependent scaling, but without discarding cross-channel relationships.
Why This Avoids the Pitfalls of AdaIN.
- No Post-Activation Reset: Unlike AdaIN, where each channel’s mean/variance is forcibly re-centered, weight demodulation never re-normalizes each activation channel in isolation.
- Preserved Relative Magnitudes: Because the filters themselves incorporate style scaling before the convolution, the resulting activations can naturally maintain the relationships among channels.
- Prevents “Spikes”: The generator no longer needs to create sharp activation peaks to reintroduce magnitude differences lost by AdaIN’s normalization.
Maintaining Style Control: Even though the normalizing step moves from the activation space to the weight space, the style vector (\(\mathbf {w}_\mathrm {latent}\)) still dictates how each channel’s contribution is scaled. This ensures layer-wise flexibility over high-level attributes (e.g., color palettes, facial geometry, textures) without imposing uniform channel normalization. By avoiding activation-based standardization, StyleGAN2 preserves rich inter-channel information, thus enabling more stable and artifact-free synthesis.
Enrichment 20.6.3.3: Noise Injection Relocation: Separating Style and Stochasticity
In StyleGAN1, spatially uncorrelated Gaussian noise was injected within the AdaIN block — directly into normalized activations. This setup caused the style vector \( w \) and the random noise to interfere in ways that were hard to control. Because both types of signals shared the same normalization path, their effects were entangled, making it difficult for the generator to cleanly separate structured semantic features (e.g., pose, facial shape) from fine-grained randomness (e.g., freckles, skin pores).
StyleGAN2 resolves this by moving the noise injection outside the style modulation block. Now, the noise is added after convolution and nonlinearity, as a purely additive operation. This isolates noise from the style-driven modulation, allowing each component to play its role without interference:
- Noise: Adds per-pixel stochastic variation — capturing non-deterministic, high-frequency effects like hair placement, pores, or skin texture.
- Style (via \( w \)): Encodes global, perceptual properties such as pose, identity, and illumination.
By decoupling noise from normalization, the generator gains more precise control over where and how randomness is applied. This reduces unintended amplification of pixel-level variation, improves training stability, and enhances interpretability of the learned style representation.
Enrichment 20.6.3.4: Path Length Regularization: Smoother Latent Traversals
While StyleGAN1 introduced the perceptual path length (PPL) as a metric — using LPIPS [778] to quantify how much the image changes under latent interpolation — StyleGAN2 builds on this idea by turning it into a regularization objective. Crucially, however, the authors abandon LPIPS (which depends on pretrained VGG features) and instead compute the gradient directly in pixel space.
Why the change? Although LPIPS correlates well with human perception, it has several drawbacks when used for regularization:
- It is computationally expensive and requires forward passes through large pretrained networks (e.g., VGG16).
- It is non-differentiable or inefficient to backpropagate through, complicating training.
- It introduces a mismatch between the generator and the external perceptual model, which may bias optimization in unintended ways.
Instead, StyleGAN2 proposes a simpler yet effective solution: directly regularize the Jacobian norm of the generator with respect to the latent vector \( \mathbf {w} \in \mathcal {W} \), computed in pixel space. The goal is to ensure that small perturbations in latent space result in proportionally smooth and stable changes in the image. The proposed path length regularization loss is: \[ \mathcal {L}_\mbox{path} = \mathbb {E}_{\mathbf {w}, \mathbf {y}} \left [ \left ( \left \| \nabla _{\mathbf {w}} G(\mathbf {w}) \cdot \mathbf {y} \right \|_2 - a \right )^2 \right ], \] where:
- \( \mathbf {y} \sim \mathcal {N}(0, I) \) is a random direction in latent space.
- \( a \) is a running average of the expected gradient norm, which centers the loss to avoid shrinking gradients to zero.
Benefits of this formulation:
- Lightweight: No need to rely on external networks or pretrained feature extractors.
- Differentiable: The pixel-space gradient is fully backpropagatable through the generator.
- Tightly coupled to training: The regularization adapts directly to the generator’s own dynamics and feature statistics.
Although pixel-space distances are not perfectly aligned with human perception (as LPIPS aims to be), as it turns out, this gradient-based regularizer effectively captures smoothness in practice. It ensures that the generator’s output changes at a steady rate along latent directions, leading to better interpolations and more reliable latent editing.
Outcome: Latent walks in StyleGAN2 produce continuous, identity-preserving morphs with reduced topological discontinuities — a key improvement over the sometimes jerky transitions seen in StyleGAN1. This lightweight regularizer thus preserves the spirit of perceptual path length while avoiding its practical limitations.
Enrichment 20.6.3.5: Lazy R1 Regularization and Evolved Loss Strategy
StyleGAN1 explored a mix of loss strategies, including Wasserstein loss with gradient penalty (WGAN-GP) [194] and the non-saturating GAN loss with R1 regularization [424]. StyleGAN2 formalizes and stabilizes this setup, adopting a consistent combination of:
- Non-saturating GAN loss for both generator and discriminator.
- Lazy one-sided gradient penalty (R1) on real samples.
- Optional path length regularization on the generator.
Discriminator Loss: The full discriminator objective is given by: \[ \mathcal {L}_{D} = - \mathbb {E}_{x \sim p_{\mbox{data}}}[\log D(x)] - \mathbb {E}_{\tilde {x} \sim p_G}[\log (1 - D(\tilde {x}))] + \delta (i \boldsymbolod N = 0) \cdot \frac {\gamma }{2} \cdot \mathbb {E}_{x \sim p_{\mbox{data}}} \left [ \|\nabla _x D(x)\|_2^2 \right ], \] where the final term is the R1 gradient penalty, applied only every \(N\) steps (typically \(N = 16\)) to reduce computational overhead.
Generator Loss: The generator minimizes the standard non-saturating loss: \[ \mathcal {L}_G = - \mathbb {E}_{\tilde {x} \sim p_G}[\log D(\tilde {x})] + \lambda _{\mbox{path}} \cdot \mathcal {L}_{\mbox{path}}, \] where \(\mathcal {L}_{\mbox{path}}\) is the path length regularization term: \[ \mathcal {L}_{\mbox{path}} = \mathbb {E}_{\mathbf {w}, \mathbf {y}} \left [ \left ( \left \| \nabla _{\mathbf {w}} G(\mathbf {w}) \cdot \mathbf {y} \right \|_2 - a \right )^2 \right ], \] with \(\mathbf {y} \sim \mathcal {N}(0, I)\) and \(a\) a running exponential average of gradient magnitudes.
Joint Optimization Logic: Despite having different loss functions, the generator \(G\) and discriminator \(D\) are trained alternatingly in an adversarial setup:
- In each training iteration, the discriminator is first updated to better distinguish real samples \(x\) from generated ones \(\tilde {x} = G(\mathbf {w})\), using \(\mathcal {L}_D\).
- Then, the generator is updated to fool the discriminator, i.e., to maximize \(D(\tilde {x})\), via \(\mathcal {L}_G\).
- Regularization terms like R1 and path length are applied at different frequencies to avoid computational bottlenecks.
This adversarial training loop leads both networks to co-evolve: the generator learns to produce realistic images, while the discriminator sharpens its ability to detect fake ones — with each providing a learning signal to the other.
Why this setup works:
- R1 avoids the interpolation overhead of WGAN-GP while regularizing gradients only near real data points.
- Lazy application of both R1 and \(\mathcal {L}_{\mbox{path}}\) allows training to scale to higher resolutions without excessive cost.
- Path length regularization improves the smoothness and predictability of the generator’s latent-to-image mapping, aiding inversion and editing tasks.
Takeaway: StyleGAN2’s adversarial training framework and especially its modular loss design — non-saturating adversarial loss, lazy R1, and optional path regularization — has become the de facto foundation for modern high-resolution GANs.
Enrichment 20.6.3.6: No Progressive Growing
Moving Away From Progressive Growing. In ProGAN and StyleGAN1, progressive growing gradually adds higher-resolution layers during training, aiming to stabilize convergence and manage memory. Despite its initial success, this approach can fix early spatial layouts in ways that cause phase artifacts, such as misaligned facial geometry (e.g., teeth remain centered to the camera rather than following the head pose). These artifacts emerge because the network’s lower-resolution layers hard-code specific spatial assumptions that later layers struggle to correct.
StyleGAN2 addresses these issues by removing progressive growing entirely and training directly at the target resolution from the outset. The architecture achieves the same coarse-to-fine benefits through more transparent and robust mechanisms:
1. Multi-Scale Skip Connections in the Generator
- RGB at Every Resolution. Each generator block outputs an RGB image at its own resolution (e.g., \(8 \times 8,\ 16 \times 16,\ \ldots ,\ 1024 \times 1024\)). These partial images are upsampled and summed to form the final output.
- Coarse to Fine in a Single Pass. Early in training, low-resolution blocks dominate the composite image, while higher-resolution blocks contribute less. As the network learns, the high-resolution outputs become more significant, refining details.
- No Opaque Fade-Ins. Instead of abruptly fading in new layers, each resolution’s contribution smoothly increases as training progresses, maintaining consistent alignment.
2. Residual Blocks in the Discriminator
- Residual Connections. The StyleGAN2 discriminator adopts a residual design, allowing inputs to bypass certain convolutions through identity (or \(1 \times 1\)) paths.
- Smooth Gradient Flow. The shortcut paths let gradients propagate effectively, even in early training, before higher-resolution features are fully meaningful.
- Flexible Depth Usage. Over time, the network learns to leverage high-resolution filters more, while the early residual connections remain available for coarse discrimination.
3. Tracking Per-Resolution Contributions The authors in [280] analyze how each resolution block affects the final output by measuring the variance of its partial RGB contribution through training. They observe:
- Early Dominance of Low-Res Layers. Initially, low-res blocks define major global structures.
- Increasing Role of High-Res Layers. As learning continues, high-resolution blocks (especially those with more channels) add finer details and sharper edges.
- Adaptive Shift Toward Detail. The model naturally transitions from coarse shapes to intricate textures without any manual “fade-in” scheduling.
Why This Redesign Matters
- Avoids Locked-In Artifacts. Without progressive growing, low-resolution layers no longer imprint rigid spatial biases that cause geometry misalignment.
- All Layers Co-Adapt. The network learns to distribute coarse and fine features simultaneously, improving semantic consistency.
- Sharper and More Stable. Multi-resolution skip connections and residual blocks make training smoother, boosting final image fidelity and detail.
- Scalable to Deep/High-Res Models. Eliminating progressive phases simplifies training when moving to ultra-high resolutions or deeper networks.
Overall, StyleGAN2’s skip+residual generator and discriminator retain the coarse-to-fine advantage of progressive growing without succumbing to phase artifacts. This shift enables more stable training and sharper, better-aligned outputs at high resolutions.
Enrichment 20.6.3.7: StyleGAN3: Eliminating Texture Sticking
StyleGAN2 excels at photorealistic image synthesis but suffers from a subtle defect: texture sticking. When performing latent interpolations or spatial transformations (e.g., translation, rotation), textures like hair or skin do not follow the global object motion. Instead, they appear anchored to fixed pixel coordinates, leading to a breakdown of equivariance—the property that image content transforms consistently with object movement.
StyleGAN3 [279] re-engineers the entire generator pipeline to ensure alias-free behavior, eliminating unintended pixel-grid reference points that cause sticking. This is achieved by treating feature maps as bandlimited continuous signals and filtering all frequency components throughout the model. As a result, StyleGAN3 generates content that moves smoothly under sub-pixel shifts and rotations, making it suitable for video, animation, and neural rendering applications.
Why Does Texture Sticking Occur? The root cause lies in how the generator in StyleGAN2 implicitly uses positional information—especially during upsampling and convolution—introducing unintentional alignment with the image grid. The generator effectively creates textures based on pixel coordinates, not object-relative positions. This limits spatial generalization and causes artifacts when the generator is expected to simulate camera motion or rotation.
How StyleGAN3 Fixes It: Core Innovations
- 1.
- Bandlimited Filtering at All Resolutions: In earlier architectures, upsampling operations (e.g., nearest-neighbor, bilinear) introduced high-frequency artifacts by duplicating or interpolating values without controlling the spectral content. These artifacts then propagated through the network, causing textures to become “anchored” to pixel grid positions. StyleGAN3 resolves this by replacing standard up/downsampling with windowed sinc filters—true low-pass filters designed to attenuate high-frequency components beyond the Nyquist limit. The filter parameters (e.g., cutoff frequency, transition bandwidth) are tuned per resolution level to retain only the frequencies that the current scale can represent reliably. This ensures that spatial detail is consistent and alias-free across all scales.
- 2.
- Filtered Nonlinearities: Pointwise nonlinearities like LeakyReLU are known to introduce sharp spectral edges, generating high-frequency harmonics even when their inputs are smooth. These harmonics can cause aliasing when passed into lower-resolution branches or subsequent convolutions. StyleGAN3 inserts a filtering step around each nonlinearity: \[ \mbox{Upsample} \;\rightarrow \; \mbox{Activate} \;\rightarrow \; \mbox{Low-pass Filter} \;\rightarrow \; \mbox{Downsample}. \] This structure ensures that the nonlinear transformation doesn’t introduce frequency components that cannot be represented at the given resolution. As a result, each block only processes and propagates bandlimited signals, preserving translation and rotation equivariance throughout the network.
- 3.
- Fourier Feature Input and Affine Spatial Transforms: In StyleGAN2, the generator begins from a fixed, learnable \( 4 \times 4 \) tensor, which is inherently tied to the pixel grid. This gives the network a built-in “origin” and orientation, which can subtly leak positional information into the generated image. StyleGAN3 replaces this with a set of Fourier features—spatially continuous sinusoidal patterns encoding different frequencies. These features are not fixed but undergo an affine transformation (rotation and translation) controlled by the first latent vector \( \mathbf {w}_0 \). This change removes the generator’s reliance on the pixel grid and introduces a trainable coordinate system based on object geometry. As a result, spatial operations (like rotating or translating the input) correspond to smooth, meaningful changes in the generated image, supporting equivariant behavior even under subpixel movements.
- 4.
- Equivariant Kernel Design: In rotationally equivariant variants (e.g., StyleGAN3-R), convolutions are restricted to \(1 \times 1\) or radially symmetric kernels, ensuring that learned filters do not introduce directionality or grid-aligned bias.
- 5.
- No Skip Connections or Noise Injection: Intermediate skip-to-RGB pathways and stochastic noise injection are removed, both of which previously introduced fixed spatial bias. Instead, StyleGAN3 allows positional information to flow only via controlled transformations.
Training Changes and Equivariance Goals
- The Perceptual Path Length regularization (\(\mathcal {L}_\mbox{path}\)) from StyleGAN2 is removed, since it penalizes motion-equivariant generators by enforcing consistent change magnitudes in pixel space.
- StyleGAN3 achieves translation equivariance in the “T” configuration and rotation+translation equivariance in “R”. This makes it ideal for unaligned datasets (e.g., FFHQ-Unaligned) and motion synthesis.
Latent and Spatial Disentanglement While StyleGAN3 retains the original \( \mathcal {W} \) and StyleSpace (\( \mathcal {S} \)) representations, studies (e.g., [4]) show that:
- Editing in \(\mathcal {S}\) remains the most disentangled.
- Unaligned generators tend to entangle pose with other attributes, so pseudo-alignment (fixing \(w_0\)) or using an aligned generator with explicit spatial transforms (\(r, t_x, t_y\)) is recommended for editing.
- In videos: Texture sticking is almost entirely gone. Hairs, wrinkles, and facial features follow object movement.
- In interpolation: Latent traversals produce realistic and continuous changes, even under subpixel jitter.
- In inversion and editing: Real images can be reconstructed and manipulated with higher spatial coherence using encoders trained on aligned data and StyleGAN3’s affine spatial parameters.
Official code and models: https://github.com/NVlabs/stylegan3
Takeaway StyleGAN3 resolves one of the most persistent issues in GAN-generated motion: positional artifacts caused by grid alignment. Through a careful redesign grounded in signal processing, it enables truly equivariant, high-quality, and temporally consistent image generation—laying the foundation for advanced video editing, scene control, and neural rendering.
Enrichment 20.7: Conditional GANs: Label-Aware Image Synthesis
Conditional GANs (cGANs) [435] enhance the classic GAN framework by incorporating structured inputs—such as class labels—into both the generator and discriminator. The motivation is clear: standard GANs produce samples from a learned distribution without any explicit control. If one wants to generate, say, only images of cats or digit “3” from MNIST, standard GANs offer no direct way to enforce that condition.
By injecting label information, cGANs enable class-conditional synthesis. The generator learns to produce samples \( G(z \mid y) \) that match a desired label \(y\), while the discriminator learns to assess whether a given sample is both real and label-consistent. This label-aware feedback significantly enhances training signals and improves controllability, quality, and diversity of generated samples.
Enrichment 20.7.1: Conditional Batch Normalization (CBN)
Conditional Batch Normalization (CBN) [136] is a key technique that enables GANs to incorporate class information not just at the input level, but deep within the generator’s layers. Unlike naive conditioning methods—such as concatenating the label vector \( y \) with the latent code \( z \)—CBN injects label-specific transformations throughout the network, significantly improving class control and generation quality.
Motivation In the vanilla GAN setup, the generator learns a mapping from noise \( z \) to image \( x \), i.e., \( G(z) \approx x \). But what if we want \( G(z \mid y) \approx x_y \), an image from a specific class \( y \)? Concatenating \( y \) with \( z \) only conditions the generator’s first layer. What happens afterward is left unregulated—there is no guarantee that the network will retain or meaningfully use the label signal. This is especially problematic in deep generators. CBN solves this by embedding the label \( y \) into every normalization layer of the generator.
This ensures that class information continually modulates the internal feature maps across layers, guiding the generation process at multiple scales.
How CBN Works Let \( x \) be the input feature map to a BatchNorm layer. In standard BatchNorm, we normalize and then apply learned scale and shift: \[ \mathrm {BN}(x) = \gamma \cdot \frac {x - \mu }{\sigma } + \beta \]
CBN replaces the static \( \gamma \) and \( \beta \) with label-dependent values \( \gamma _y \) and \( \beta _y \), often produced via a small embedding or MLP based on \( y \): \[ \mathrm {CBN}(x \mid y) = \gamma _y \cdot \frac {x - \mu }{\sigma } + \beta _y \]
Here, each class \( y \) learns its own affine transformation parameters. This leads to class-specific modulation of normalized features—effectively injecting semantic ”style” throughout the generator.
- CBN allows for a shared generator backbone, with only minor per-class differences through \( \gamma _y \) and \( \beta _y \).
- During training, these class-specific affine parameters are learned jointly with the generator weights.
- CBN does not increase the number of convolutions but dramatically boosts the expressiveness of conditional generation.
CBN in the Generator Conditional Batch Normalization (CBN) introduces class information deep into the generator. At each layer \( \ell \), the activations are batch-normalized and then rescaled using label-specific parameters \( \gamma _y^\ell \), \( \beta _y^\ell \), allowing each class to modulate the feature flow independently across scales.
Enrichment 20.7.1.1: Projection-Based Conditioning in Discriminators
While Conditional Batch Normalization (CBN) is highly effective for injecting label information into the generator, it is rarely applied in the discriminator. The discriminator’s primary responsibility is to distinguish real from fake images and verify that they match the target label \( y \). Rather than applying class-specific transformations to every layer, conditional information is typically injected via architectural conditioning, using either:
- Concatenation-Based Conditioning: The one-hot label \( y \) is spatially expanded and concatenated to the input image \( x \in \mathbb {R}^{3 \times H \times W} \), resulting in a combined tensor \( [x; y'] \in \mathbb {R}^{(3+C) \times H \times W} \), where \( C \) is the number of classes. While simple, this method weakens in deeper layers, where the label signal may vanish.
-
Projection Discriminator [438]: A more robust alternative that introduces label conditioning directly into the discriminator’s output logit. The logit is defined as: \[ \underbrace {D(x, y)}_{\mbox{class-aware score}} = \underbrace {b(x)}_{\mbox{realism term}} + \underbrace {h(x)^\top e(y)}_{\mbox{semantic match}}, \] where:
- \( h(x) \in \mathbb {R}^d \) is a global feature vector extracted from the image (after convolution and pooling).
- \( e(y) \in \mathbb {R}^d \) is a learned embedding vector for the class label \( y \).
- \( b(x) = w^\top h(x) \) is a standard linear layer predicting the realism of \( x \), independent of label.
This design cleanly separates visual quality from semantic alignment.
Advantages of Projection-Based Conditioning:
- Efficiency: Requires only one additional dot product at the final layer, with minimal parameter overhead.
- Interpretability: Clearly decomposes the output into realism and semantic compatibility terms.
- Scalability: Works well for large-scale datasets and deep discriminators (e.g., BigGAN which we’ll cover later).
By combining this strategy with techniques like Spectral Normalization (discussed next), projection-based discriminators remain stable even under high capacity settings and offer strong guidance for conditional image synthesis.
Enrichment 20.7.1.2: Training Conditional GANs with CBN
Conditional GANs (cGANs) trained with Conditional Batch Normalization (CBN) aim to synthesize images that are not only visually realistic, but also semantically aligned with a given class label \( y \). To achieve this, the generator and discriminator are trained in tandem, each using label information differently.
Generator \( G(z, y) \): Label-Aware Synthesis The generator receives a latent code \( z \sim \mathcal {N}(0, I) \) and a class label \( y \). The label modulates every normalization layer via CBN: \[ \mathrm {CBN}(x \mid y) = \gamma _y \cdot \frac {x - \mu }{\sigma } + \beta _y \] This injects label-specific transformations into the generator’s internal feature maps, allowing class control at multiple spatial scales. The output image is: \[ \tilde {x} = G(z, y) \]
Discriminator \( D(x, y) \): Realness and Label Consistency The discriminator receives both an image \( x \) and its associated label \( y \), and outputs a scalar score that jointly reflects:
- Whether the image looks real (i.e., sampled from \( p_{\mbox{data}} \) rather than the generator).
- Whether it is semantically consistent with the provided label \( y \).
This dual-role is often realized using a projection discriminator [438], where the label is embedded and combined with the discriminator’s internal features:
\[ D(x, y) = b(x) + h(x)^\top e(y) \]
Here, \( h(x) \) is a learned feature embedding from the image, \( e(y) \) is the learned embedding of the label \( y \), and \( b(x) \) is a base logit representing the visual realism of \( x \). The dot product term encourages semantic agreement between the image and the label — if \( h(x) \) and \( e(y) \) align well, \( D(x, y) \) increases.
Training Pipeline with CBN Conditioning: The Conditional GAN training loop is fully differentiable and jointly optimizes two objectives: (1) realism — fooling the discriminator into classifying fake images as real, and (2) semantic alignment — ensuring that generated images match the assigned class label. Conditional Batch Normalization (CBN) plays a key role in achieving this alignment by embedding the label \( y \) throughout the generator.
- 1.
- Sample Inputs: For each batch:
- Sample latent codes \( z^{(i)} \sim \mathcal {N}(0, I) \) and corresponding labels \( y^{(i)} \in \{1, \dots , K\} \).
- 2.
- Generate Conditioned Fakes: For each \( (z^{(i)}, y^{(i)}) \), generate a fake image: \[ \tilde {x}^{(i)} = G(z^{(i)}, y^{(i)}) \] The generator uses CBN at every layer to condition on \( y^{(i)} \), ensuring class-relevant features are injected at all depths.
- 3.
- Discriminator Update:
- For real images \( x^{(i)} \sim p_{\mbox{data}}(x \mid y^{(i)}) \), the discriminator \( D(x^{(i)}, y^{(i)}) \) should output a high value, indicating high confidence that the image is real and belongs to class \( y^{(i)} \).
- For fake images \( \tilde {x}^{(i)} \), the discriminator \( D(\tilde {x}^{(i)}, y^{(i)}) \) should output a low value, identifying them as generated (and potentially misaligned with \( y^{(i)} \)).
- 4.
- Loss Functions:
- Discriminator: \[ \mathcal {L}_D = -\frac {1}{N} \sum _{i=1}^N \log D(x^{(i)}, y^{(i)}) \; - \; \frac {1}{N} \sum _{i=1}^N \log \left ( 1 - D(\tilde {x}^{(i)}, y^{(i)}) \right ) \] The first term is minimized when real samples are confidently classified as real \((D(x, y) \to 1)\), while the second is minimized when fake samples are correctly rejected \((D(\tilde {x}, y) \to 0)\).
- Generator: \[ \mathcal {L}_G = -\frac {1}{N} \sum _{i=1}^N \log D(\tilde {x}^{(i)}, y^{(i)}) \] The generator is optimized to maximize the discriminator’s belief that its outputs are real and consistent with label \( y^{(i)} \) — hence minimizing the negative log-likelihood encourages \( D(\tilde {x}, y) \to 1 \).
- 5.
- Backpropagation: Gradients are computed and propagated through both the standard network layers and the label-conditioned affine parameters in CBN. This teaches the generator to match label semantics at multiple feature levels, and the discriminator to enforce both realism and label consistency.
- The logarithmic terms act as soft penalties: \[ \log D(x, y) \to 0 \mbox{ if } D(x, y) \to 1 \quad \mbox{(real images correct)} \] \[ \log (1 - D(\tilde {x}, y)) \to 0 \mbox{ if } D(\tilde {x}, y) \to 0 \quad \mbox{(fake images rejected)} \]
- Similarly, the generator aims to push \( D(\tilde {x}, y) \to 1 \), making \(\log D(\tilde {x}, y) \to 0\), which occurs when the discriminator is fooled — i.e., when the generated image is both realistic and label-consistent.
This adversarial setup enforces both high-fidelity and class-conditioned generation. However, without regularization, it can suffer from unstable gradients, overconfident discriminators, and poor generalization — issues we’ll now get into.
Limitations of CBN-Only Conditioning While CBN provides powerful class control, it comes with caveats:
- Shortcut Learning: The generator might ignore the noise vector \( z \), reducing output diversity.
- Overfitting to Labels: CBN parameters \( (\gamma _y, \beta _y) \) may overfit when class distributions are imbalanced.
- Training Instability: Without constraints, the discriminator may overemphasize labels at the cost of visual quality.
To address these issues, the next section introduces Spectral Normalization [438]—a principled method for controlling the discriminator’s capacity and improving the stability of conditional GAN training.
Enrichment 20.7.2: Spectral Normalization for Stable GAN Training
Spectral Normalization (SN) [438] is a technique designed to stabilize GAN training by constraining the Lipschitz constant of the discriminator. This is achieved by directly controlling the largest singular value—also known as the spectral norm—of each weight matrix in the network. By normalizing the spectral norm to a fixed value (typically 1), SN ensures that no layer can amplify the norm of its input arbitrarily.
Why Lipschitz Constraints Help. The training of GANs involves a two-player minimax game between a discriminator \( D \) and a generator \( G \). The discriminator is trained to distinguish real data from fake samples generated by \( G \), using an objective such as: \[ \mathcal {L}_D = -\mathbb {E}_{x \sim p_{\mathrm {data}}} [\log D(x)] \;-\; \mathbb {E}_{z \sim p(z)}[\log (1 - D(G(z)))]. \] If the discriminator is too flexible—particularly if its output varies too rapidly in response to small input perturbations—it can easily overfit, confidently separating real and fake data. In this regime, the generator receives vanishing gradients: once \( D \) becomes near-perfect, it ceases to provide useful learning signals, and \( \nabla _G \approx 0 \). This leads to generator collapse and training instability.
To prevent this, we can restrict the class of discriminator functions to those with bounded sensitivity. More formally, we enforce a 1-Lipschitz (or \( K \)-Lipschitz) constraint: for all inputs \( x_1, x_2 \), \[ \| D(x_1) - D(x_2) \| \leq K \|x_1 - x_2\| \] This condition ensures that the discriminator behaves smoothly—its outputs cannot change faster than a controlled rate with respect to input variation. Under such a constraint, gradients passed to the generator remain informative and well-scaled throughout training.
But how can we impose this constraint practically, especially when the discriminator is a deep neural network composed of many weight matrices? The answer lies in analyzing how each linear layer scales input vectors—and that leads us directly to a set of mathematical tools designed to measure such transformations: eigenvalues, singular values, and ultimately, the spectral norm.
To understand these ideas rigorously, we begin by revisiting a fundamental concept from linear algebra: eigenvalues and eigenvectors.
Enrichment 20.7.2.1: Spectral Normalization - Mathematical Background
Eigenvalues and Eigenvectors: Invariant Directions in Linear Maps Given a square matrix \( A \in \mathbb {R}^{n \times n} \), an eigenvector \( v \in \mathbb {R}^n \) is a non-zero vector that, when transformed by \( A \), results in a scaled version of itself: \[ A v = \lambda v \] where \( \lambda \in \mathbb {R} \) (or \( \mathbb {C} \)) is the corresponding eigenvalue. Geometrically, this means that the action of \( A \) leaves the direction of \( v \) unchanged—only its length is scaled by \( \lambda \). In contrast to general vectors that may be rotated, skewed, or fully transformed, eigenvectors identify the matrix’s “fixed” directions of behavior, and eigenvalues quantify how strongly each of those directions is scaled.
These pairs \( (\lambda , v) \) play a fundamental role in understanding the internal structure of linear transformations. For example, they describe the principal modes along which a system stretches or compresses space, and they allow us to determine whether a transformation is stable, reversible, or diagonalizable. In systems theory, optimization, and neural network analysis, they reveal how signals are amplified or attenuated by repeated application of a layer or operator.
To compute eigenvalues, we rearrange the eigenvector equation as \( (A - \lambda I)v = 0 \), which admits non-trivial solutions only when \( \det (A - \lambda I) = 0 \). This gives the characteristic polynomial of \( A \), whose roots are the eigenvalues. Once we solve for \( \lambda \), we can substitute it back and solve \( (A - \lambda I)v = 0 \) to find the corresponding eigenvectors \( v \).
Here is a basic numerical example in Python:
import numpy as np
A = np.array([[2, 1],
[1, 2]])
eigvals, eigvecs = np.linalg.eig(A)
# Print eigenvalues
print("Eigenvalues:")
for i, val in enumerate(eigvals):
print(f" lam{i + 1} = {val:.6f}")
# Print eigenvectors
print("\nEigenvectors (each column is a vector):")
for i in range(eigvecs.shape[1]):
vec = eigvecs[:, i]
print(f" v{i + 1} = [{vec[0]:.6f}, {vec[1]:.6f}]")Results for this:
Eigenvalues:
lam1 = 3.000000
lam2 = 1.000000
Eigenvectors(each column is a vector):
v1 = [0.707107, 0.707107]
v2 = [-0.707107, 0.707107]Why is this relevant to GANs, or to neural networks more broadly? Each linear layer in a network is defined by a weight matrix \( W \), which transforms input vectors as \( x \mapsto Wx \). The key question is: how much can \( W \) amplify the norm of its input? If certain directions are stretched excessively, the network becomes unstable—gradients may explode, and outputs may become overly sensitive to small input changes. If other directions are collapsed, information is lost and gradients vanish.
Eigenvalues help quantify this behavior in square, symmetric matrices: the largest eigenvalue reflects the maximum scaling factor applied in any direction. In such cases, bounding the largest eigenvalue effectively bounds the transformation’s ability to distort inputs. This idea connects directly to the concept of Lipschitz continuity, which constrains how sensitive a function is to perturbations in its input. For a function \( f \) to be \( K \)-Lipschitz, we must have \( \|f(x_1) - f(x_2)\| \leq K \|x_1 - x_2\| \) for all \( x_1, x_2 \). In the case of the WGAN-GP optimization objective, being constrained in that way is crucial for ensuring gradient stability and generalization.
In the case of a linear transformation, the Lipschitz constant is exactly the operator norm of the matrix \( W \), i.e., the maximum value of \( \|Wx\| / \|x\| \) over all non-zero \( x \).
For square matrices, this coincides with the largest singular value. Spectral normalization leverages this insight: by explicitly normalizing \( W \) so that its largest singular value—also called its spectral norm—is 1, we guarantee that the linear component of the layer is 1-Lipschitz.
A natural follow-up question is whether this guarantee still holds after applying the layer’s nonlinearity, such as ReLU. Indeed, activation functions also influence the Lipschitz constant. Some nonlinearities, like sigmoid or tanh, can shrink or saturate outputs, leading to norm compression or gradient vanishing. However, ReLU and most of its variants (e.g., Leaky ReLU) are 1-Lipschitz compliant: applying them to a vector cannot increase its norm. Therefore, when using ReLU-based activations in conjunction with spectrally normalized linear layers, the composition preserves the Lipschitz bound. This makes the entire layer (linear + activation) 1-Lipschitz, ensuring stable gradients and reliable signal propagation.
Since eigenvalue analysis provides a structured way to understand how matrices scale vectors, it serves as the conceptual precursor to the singular value decomposition (SVD)—a generalization that extends these ideas to arbitrary matrices, including those that are non-square and non-symmetric. SVD and spectral norm estimation will form the mathematical core of spectral normalization, and enable its application to deep convolutional networks and GAN discriminators.
Singular Value Decomposition (SVD): Structure and Signal in Data Singular Value Decomposition (SVD) is one of the most widely used and interpretable tools in linear algebra, especially when applied to data analysis. It provides a principled way to factorize any real matrix \( X \in \mathbb {R}^{n \times m} \) into three matrices that expose its internal structure—how it stretches, rotates, and reprojects the data. SVD serves as a foundation for many modern machine learning algorithms and dimensionality reduction techniques.
At a high level, SVD can be seen as a data-driven generalization of the Fourier Transform. Whereas the Fourier basis decomposes signals into global sinusoidal modes that are independent of the data, the SVD basis is tailored to the actual dataset. It adapts to the underlying structure of \( X \), identifying key directions—patterns, features, or modes—that explain most of the variation in the data. This same decomposition underlies Principal Component Analysis (PCA), where the goal is to find orthogonal directions (principal components) along which the data exhibits maximum variance. While PCA specifically centers and projects the data to find these components, SVD applies to any matrix directly—making it more general.
The utility of SVD goes far beyond mathematical elegance. It is used everywhere: in image compression, facial recognition, search engine ranking algorithms, natural language processing, and recommendation systems like those at Amazon or Netflix. There, rows may represent customers, columns may represent movies, and the entries in \( X \) quantify viewing history. SVD can identify latent structures—such as genres or interest patterns—that drive behavior. What makes SVD powerful is not just that it works, but that the components it reveals are often understandable and interpretable. It transforms complex, high-dimensional data into structured modes we can visualize, analyze, and act on. Even better, it is scalable to massive datasets through efficient numerical algorithms.
For a practical and intuitive introduction to these concepts, including real Python code and visual explanations, we highly recommend Steve Brunton’s excellent video series on Singular Value Decomposition and PCA from the University of Washington. The following summary builds on most of its ideas.
SVD: Structure, Meaning, and Application to Real-World Data To make this concrete, consider two real-world examples of data matrices \( X \). In the first, suppose we have a dataset consisting of face images, each stored as a column vector. If each image is grayscale and of size \( H \times W \), then after flattening, each column \( x_i \in \mathbb {R}^n \), where \( n = H \cdot W \). Stacking \( m \) such vectors side by side yields a matrix \( X \in \mathbb {R}^{n \times m} \), where \( n \gg m \). This is a “tall and skinny” matrix where each column represents one person’s face. Performing SVD on this matrix allows us to extract spatial modes across all the faces—patterns like edges, contours, or lighting variations—allowing for data compression, denoising, and the generation of new faces from a reduced latent basis.
In the second example, consider a simulation of fluid flow past a circular object. Each column of the matrix \( X \in \mathbb {R}^{n \times m} \) now represents the velocity field (or pressure field) at a particular time step, flattened into a vector. As the fluid evolves in time, the state changes, so each column \( x_i \) captures the system’s dynamics at time \( t_i \). Here, SVD reveals the dominant coherent structures in the flow—vortex shedding patterns, boundary layer oscillations, and so on—distilled into interpretable spatial modes. In both cases, SVD helps convert a high-dimensional system into a compact and meaningful representation.
The SVD of any real matrix \( X \in \mathbb {R}^{n \times m} \) (with \( n \geq m \)) always exists and takes the form: \[ X = U \Sigma V^\top \] Here, \( U \in \mathbb {R}^{n \times n} \) and \( V \in \mathbb {R}^{m \times m} \) are orthonormal matrices, meaning their columns are orthogonal, and they have a unit length. Algebraically, this means: \[ U^\top U = UU^\top = I_{n \times n}, \qquad V^\top V = VV^\top = I_{m \times m} \] Each set of vectors in \( U \) and \( V \) forms a complete orthonormal basis for its respective space. The columns of \( U \) span the column space of \( X \), and the columns of \( V \) span the row space. While these matrices can be interpreted geometrically as rotations or reflections that preserve norms and angles, their real significance lies in the fact that they provide a new basis tailored to the data itself.
The left singular vectors in \( U \) have the same dimensionality as the columns of \( X \), and they can be thought of as data-specific “eigen-basis” elements. In the face image example, the vectors \( u_1, u_2, \ldots \) correspond to eigenfaces—representative spatial patterns that appear repeatedly across different faces. These might reflect things like lighting patterns, face shape contours, or common structural differences. In the fluid dynamics example, the \( u_i \) represent eigen flow-fields—dominant patterns in how fluid velocity or pressure changes over time. These basis vectors are not arbitrary: they are orthonormal directions derived from the data that best capture variance across the dataset. Crucially, only the first \( m \) columns of \( U \) are used in the decomposition, since the rank of \( X \in \mathbb {R}^{n \times m} \) is at most \( m \). These \( u_i \) vectors are sorted according to their importance in capturing variance, meaning \( u_1 \) is more important than \( u_2 \), and so on.
The matrix \( \Sigma \in \mathbb {R}^{n \times m} \) is diagonal and contains the singular values \( \sigma _1, \ldots , \sigma _m \), followed by trailing zeros if \( n > m \). It has the form: \[ \Sigma = \begin {bmatrix} \sigma _1 & 0 & \cdots & 0 \\ 0 & \sigma _2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma _m \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \end {bmatrix}_{n \times m}, \qquad \mbox{with } \sigma _1 \geq \sigma _2 \geq \cdots \geq \sigma _m \geq 0 \] These singular values tell us how much variance or “energy” each corresponding mode captures from the data. In fact, the total energy in the matrix—measured as the squared Frobenius norm—is the sum of the squared singular values: \[ \|X\|_F^2 = \sum _{i=1}^m \sigma _i^2 \] Hence, the first few singular values usually dominate, and \( \sigma _1^2 / \|X\|_F^2 \) gives the fraction of total variance captured by the first mode.
We can express the full decomposition explicitly as a sum of rank-one outer products: \[ X = \sum _{i=1}^{r} \sigma _i u_i v_i^\top \] where \( r = \mbox{rank}(X) \), and \( u_i \in \mathbb {R}^n \), \( v_i \in \mathbb {R}^m \) are the \( i \)-th left and right singular vectors. Each term \( \sigma _i u_i v_i^\top \) represents a matrix of rank one that contributes to reconstructing \( X \). These terms are not just additive: they are ordered so that each successive mode contributes less to the matrix’s variance.
To reconstruct a specific data point \( x_i \)—that is, the \( i \)-th column of the data matrix \( X \)—we combine the shared spatial modes \( u_1, \ldots , u_m \) using weights derived from the matrix product \( \Sigma V^\top \). Each vector \( u_j \) contributes a particular spatial pattern, and the coefficients that determine how to mix them to recover \( x_i \) are drawn from the \( i \)-th column of \( \Sigma V^\top \). This can be written explicitly as: \[ x_i = \sum _{j=1}^{m} \sigma _j u_j v_{j,i} \] where \( v_{j,i} \) is the entry in row \( j \), column \( i \) of \( V \), and \( \sigma _j v_{j,i} \) reflects the scaled contribution of mode \( u_j \) to sample \( x_i \). This formulation always holds, but its interpretation depends on the nature of the data encoded in \( X \).
In static datasets like facial images—where each column \( x_i \) represents a different face—the interpretation is sample-centric. The vectors \( u_1, \ldots , u_m \) are shared spatial modes, or eigenfaces, and each face \( x_i \) is a specific mixture of them. The weights that determine this mixture are found in the \( i \)-th column of \( V^\top \), or equivalently the \( i \)-th row of \( V \). Each such row tells us how much of each spatial mode to include when reconstructing the corresponding face. The singular values in \( \Sigma \) scale these weights to reflect the global importance of each mode. In other words, \( V^\top \) tells us how to linearly combine the shared features \( u_1, \ldots , u_m \) to form each image in the dataset.
In time-evolving physical systems, such as fluid flow simulations, the interpretation is reversed: the dataset \( X \) consists of snapshots of the system’s state at different times. Each column \( x_i \) corresponds to the system’s configuration at time \( t_i \). In this setting, the \( i \)-th column of \( V \) describes how strongly the \( i \)-th spatial mode \( u_i \) is activated at each time step. That is, each \( v_i \in \mathbb {R}^m \) forms a temporal profile—or an eigen time-series—that quantifies how mode \( u_i \) varies throughout time. In this case, each \( u_i \) represents a coherent spatial structure (e.g., a vortex or shear layer), and the corresponding \( v_i \) tells us when and how that structure appears across the sequence of system states.
In both interpretations, the combination of \( U \), \( \Sigma \), and \( V \) enables a powerful and interpretable reconstruction of the original data. The matrix \( U \) defines spatial structures shared across samples or time, the matrix \( V \) tells us either how to mix those structures for each observation (static data) or how the structures evolve temporally (dynamic data), and \( \Sigma \) modulates their importance.
This distinction is crucial for understanding SVD as a data-driven basis decomposition tailored to the geometry and temporal structure of the dataset.
When some singular values \( \sigma _i \) are very small—indicating low energy or negligible contribution—we can truncate the decomposition to retain only the top \( r \) modes:
\[ X \approx \sum _{i=1}^{r} \sigma _i u_i v_i^\top \]
This yields a rank-\( r \) approximation of \( X \) that captures the dominant structure while ignoring negligible details. This approximation is not just convenient—it is provably optimal in the Frobenius norm sense. That is, among all rank-\( r \) matrices \( \tilde {X} \in \mathbb {R}^{n \times m} \), the truncated SVD minimizes the squared error: \[ \|X - \tilde {X}\|_F \geq \left \|X - \sum _{i=1}^{r} \sigma _i u_i v_i^\top \right \|_F \] This optimality is fundamental to many applications in data science, including dimensionality reduction, matrix compression, and feature extraction.
Spectral Structure via \( X^\top X \) and \( XX^\top \) To better understand why the SVD always exists and how it connects to fundamental linear algebra operations, recall that for any real matrix \( X \in \mathbb {R}^{m \times n} \), both \( X^\top X \in \mathbb {R}^{n \times n} \) and \( XX^\top \in \mathbb {R}^{m \times m} \) are symmetric and positive semi-definite. This means:
- They can be diagonalized via eigendecomposition: \( X^\top X = V \Lambda V^\top \), \( XX^\top = U \Lambda U^\top \).
- Their eigenvalues are real and non-negative.
The Singular Value Decomposition leverages these eigendecompositions. Specifically, the right singular vectors \( V \) are the eigenvectors of \( X^\top X \), while the left singular vectors \( U \) are the eigenvectors of \( XX^\top \). The non-zero eigenvalues \( \lambda _i \) of either matrix are equal and relate to the singular values as \( \sigma _i = \sqrt {\lambda _i} \).
Economy (or Truncated) SVD When \( \mbox{rank}(X) = r < \min (m, n) \), we can simplify the decomposition by using only the top \( r \) singular values and their associated singular vectors. This yields the so-called economy SVD: \[ X \approx \hat {U} \hat {\Sigma } \hat {V}^\top \] where:
- \( \hat {U} \in \mathbb {R}^{m \times r} \) contains the top \( r \) left singular vectors (columns of \( U \)),
- \( \hat {\Sigma } \in \mathbb {R}^{r \times r} \) is a diagonal matrix with the top \( r \) singular values,
- \( \hat {V} \in \mathbb {R}^{n \times r} \) contains the top \( r \) right singular vectors (columns of \( V \)).
This truncated representation captures the most significant directions of variance or information in \( X \), and is especially useful in dimensionality reduction, PCA, and low-rank approximations.
How is SVD Computed in Practice? Although the SVD is defined mathematically via the factorization \( X = U \Sigma V^\top \), computing it in practice follows a conceptually clear pipeline that is closely tied to eigendecomposition. Here is a high-level outline of how the singular values and vectors of a real matrix \( X \in \mathbb {R}^{m \times n} \) can be computed:
- 1.
- Form the symmetric, positive semi-definite matrices \( X^\top X \in \mathbb {R}^{n \times n} \) and \( XX^\top \in \mathbb {R}^{m \times m} \).
- 2.
- Compute the eigenvalues \( \lambda _1, \ldots , \lambda _r \) of \( X^\top X \) by solving the characteristic equation: \[ \det (X^\top X - \lambda I) = 0 \] This polynomial equation of degree \( n \) yields all the eigenvalues of \( X^\top X \). In most practical algorithms, direct determinant expansion is avoided, and iterative numerical methods (e.g., the QR algorithm) are used for greater stability.
- 3.
- For each eigenvalue \( \lambda _i \), compute the corresponding eigenvector \( v_i \in \mathbb {R}^n \) by solving the homogeneous system: \[ (X^\top X - \lambda _i I) v_i = 0 \] This involves finding a nontrivial solution in the nullspace of the matrix \( X^\top X - \lambda _i I \).
- 4.
- The singular values \( \sigma _i \) are then obtained as the square roots of the eigenvalues: \[ \sigma _i = \sqrt {\lambda _i} \] These are placed in decreasing order along the diagonal of \( \Sigma \), capturing how strongly \( X \) stretches space along each mode.
- 5.
- The right singular vectors \( v_i \) form the columns of \( V \). To recover the corresponding left singular vectors \( u_i \), we use the relation: \[ u_i = \frac {1}{\sigma _i} X v_i \] for all \( \sigma _i \neq 0 \). This ensures orthonormality between the columns of \( U \) and links the left and right singular vectors through the action of \( X \).
While this approach is instructive, explicitly computing \( X^\top X \) or \( XX^\top \) is rarely done in modern numerical practice, especially for large or ill-conditioned matrices, because squaring the matrix amplifies numerical errors and can destroy low-rank structure.
Instead, standard libraries use more stable and efficient algorithms based on bidiagonalization. The most prominent is the Golub–Kahan SVD algorithm, which proceeds in two stages:
- First, \( X \) is orthogonally transformed into a bidiagonal matrix using Householder reflections.
- Then, iterative eigen-solvers (such as the QR algorithm or Divide-and-Conquer strategy) are applied to the bidiagonal form to extract the singular values and vectors.
Other methods include the Golub–Reinsch algorithm for computing the full SVD and Lanczos bidiagonalization for sparse or low-rank approximations.
Curious readers who want to dive deeper into these techniques are encouraged to consult:
- Matrix Computations by Golub and Van Loan — especially Chapters 8–10 (full SVD, QR-based bidiagonalization, and Divide-and-Conquer methods).
- Numerical Linear Algebra by Trefethen and Bau — particularly the discussion on the numerical stability of SVD versus eigendecomposition.
- LAPACK’s online documentation — detailing routines like dgesvd (full SVD) and dgesdd (Divide-and-Conquer SVD).
Understanding how these algorithms work and when to apply them is critical for large-scale scientific computing, dimensionality reduction, and neural network regularization techniques like spectral normalization.
Nevertheless, for practitioners who simply want to apply SVD in real-world problems—having understood its purpose and how to interpret its results—modern scientific computing libraries make it easy to compute with just a few lines of code.
For example, in Python with NumPy or SciPy:
import numpy as np
# Create an example matrix X
X = np.random.randn(100, 50) # Tall-and-skinny matrix
# Compute the full SVD
U, S, Vt = np.linalg.svd(X, full_matrices=True)
# U: left singular vectors (100x100)
# S: singular values (vector of length 50)
# Vt: transpose of right singular vectors (50x50)Alternatively, to compute a truncated or low-rank approximation (economy SVD), you can use:
from scipy.linalg import svd
# Compute economy-sized SVD (faster for large problems)
U, S, Vt = svd(X, full_matrices=False)This approach is widely used in machine learning pipelines, signal processing, recommendation systems, and dimensionality reduction algorithms such as PCA. Efficient and scalable variants also exist for sparse or streaming data matrices.
Finally, we also get why SVD is guaranteed to exist for any real matrix. Another interesting property of SVD is that it is unique up to signs: for each pair \( (u_i, v_i) \), flipping their signs simultaneously leaves the outer product \( u_i v_i^\top \) unchanged. This sign ambiguity does not affect reconstruction, but it is important to be aware of when analyzing the components numerically.
In the context of deep learning, these insights become practically useful. The largest singular value \( \sigma _1 \), also known as the spectral norm, determines the maximum amplification that a linear transformation can apply to an input vector. Spectral normalization takes advantage of this by enforcing an upper bound on the spectral norm of a weight matrix—ensuring that networks remain stable, gradients do not explode, and the Lipschitz continuity of the model is preserved. This plays a critical role in training robust GANs and other adversarial models.
Finally, we also get why SVD is guaranteed to exist for any real matrix. Another interesting property of SVD is that is unique up to signs: for each pair \( (u_i, v_i) \), flipping their signs simultaneously leaves the outer product \( u_i v_i^\top \) unchanged. This sign ambiguity does not affect reconstruction, but it is important to be aware of when analyzing the components numerically.
In the context of deep learning, these insights become practically useful. The largest singular value \( \sigma _1 \), also known as the spectral norm, determines the maximum amplification that a linear transformation can apply to an input vector. Spectral normalization takes advantage of this by enforcing an upper bound on the spectral norm of a weight matrix—ensuring that networks remain stable, gradients do not explode, and the Lipschitz continuity of the model is preserved. This plays a critical role in training robust GANs and other adversarial models.
Spectral Norm of a Weight Matrix Let \(W \in \mathbb {R}^{m \times n}\) be the weight matrix of a NN layer. Its spectral norm \(\sigma (W)\) is its largest singular value: \[ \sigma (W) \;=\; \max _{\|v\|=1} \|Wv\|_2. \] To constrain \(\sigma (W)\) to 1, spectral normalization reparameterizes \(W\) as \(\hat {W} \;=\; \frac {\,W\,}{\,\sigma (W)\!}.\) This ensures that the layer cannot amplify an input vector’s norm by more than 1, thus bounding the discriminator’s Lipschitz constant.
Fast Spectral–Norm Estimation via Power Iteration What is the spectral norm and why that inequality is true? For any matrix \(W\) the spectral norm is defined as \[ \sigma (W)\;=\;\|W\|_{2}\;=\;\max _{\|x\|_{2}=1}\|Wx\|_{2}. \] It is the largest factor by which \(W\) can stretch a vector. If \(x\neq 0\) is arbitrary, write \(x=\|x\|_{2}\,\hat x\) with \(\|\hat x\|_{2}=1\). Then \[ \frac {\|Wx\|_{2}}{\|x\|_{2}} =\frac {\|W\hat x\|_{2}}{1} \le \max _{\|y\|_{2}=1}\|Wy\|_{2} =\sigma (W). \] Equality is achieved when \(\hat x\) is the right singular vector \(v_{1}\) corresponding to the largest singular value \(\sigma _{1}\). Thus \(\sigma (W)\) is the supreme stretch factor and every individual ratio \(\|Wx\|_{2}/\|x\|_{2}\) is bounded by it.
What power iteration is and why it works? Repeatedly multiplying any non-orthogonal vector by \(W\) and renormalising pushes the vector toward \(v_{1}\); equivalently, repeatedly multiplying by the symmetric positive-semi-definite matrix \(W^{\mathsf T}W\) pushes toward \(v_{1}\) even faster, because \(v_{1}\) is its dominant eigenvector with eigenvalue \(\sigma _{1}^{2}\). Forming \(W^{\mathsf T}W\) explicitly is expensive and unnecessary—alternating \(W^{\mathsf T}\) and \(W\) gives the same effect using only matrix–vector products.
Step-by-step (one iteration per forward pass)
- 1.
- Persistent vector: Keep a single unit vector \(u\in \mathbb {R}^{m}\). Initialise it once with random entries; after that recycle the updated \(u\) from the previous mini-batch.
- 2.
- Right–vector update. Compute \[ v \;=\; \frac {W^{\mathsf T}u}{\|W^{\mathsf T}u\|_{2}} \quad (\;v\in \mathbb {R}^{n},\ \|v\|_{2}=1\;). \]
This is one gradient-free step toward the dominant right singular vector.
- 3.
- Left–vector update: Compute \[ u \;=\; \frac {Wv}{\|Wv\|_{2}} \quad (\;\|u\|_{2}=1\;). \] After this pair of operations, \(u\) and \(v\) are better aligned with the true singular vectors \(u_{1}\) and \(v_{1}\).
- 4.
- Singular-value estimate: Evaluate \[ \hat \sigma \;=\; u^{\mathsf T}Wv \;=\;\|Wv\|_{2}. \] With the recycled \(u\) the estimate is already very accurate; a single sweep is enough in practice.
- 5.
- Weight normalisation: Scale the weight matrix once per forward pass: \[ \widehat {W} \;=\; \frac {W}{\hat \sigma }. \] Now \(\|\widehat {W}\|_{2}\approx 1\), so the layer is approximately \(1\)-Lipschitz.
Why alternate \(W^{\mathsf T}\) and \(W\)? From the SVD \(W=U\Sigma V^{\mathsf T}\) we have \(Wv_{1}=\sigma _{1}u_{1}\) and \(W^{\mathsf T}u_{1}=\sigma _{1}v_{1}\). Composing the two maps gives \(W^{\mathsf T}Wv_{1}=\sigma _{1}^{2}v_{1}\). Power iteration on \(W^{\mathsf T}W\) would therefore converge to \(v_{1}\); carrying it out implicitly via \(W^{\mathsf T}\!/\,W\) multiplication avoids the \(\mathcal {O}(mn^{2})\) cost of forming the normal matrix.
Cost in practice Each layer pays for two extra matrix–vector products and a few normalisations—tiny compared with convolution operations—yet gains a reliable on-the-fly \(\sigma (W)\) estimate that keeps gradients and adversarial training under control.
def spectral_norm_update(W, u, num_iterations=1):
# W: Weight matrix shaped [out_features, in_features]
# u: Approximated top singular vector (shape = [out_features])
for _ in range(num_iterations):
# v: top right singular vector approximation
v = W.t().mv(u)
v_norm = v.norm()
v = v / (v_norm + 1e-12)
# u: top left singular vector approximation
u_new = W.mv(v)
u_new_norm = u_new.norm()
u = u_new / (u_new_norm + 1e-12)
sigma = u.dot(W.mv(v))
# Return normalized weights and updated vectors
return W / sigma, u, vAlternative Loss: Hinge Loss Formulation While the non-saturating GAN loss is commonly used in conditional GANs with CBN, another widely adopted objective—especially in more recent setups such as this work and BigGANs—is the hinge loss we’ve covered previously with SVMs §3.6.4. It replaces the cross-entropy terms with a margin-based objective, helping the discriminator focus on classification margins and improving gradient stability.
Hinge loss (for conditional GANs) \[ \begin {aligned} \mathcal {L}_D &= \mathbb {E}_{x \sim p_{\mbox{data}}} \left [ \max (0, 1 - D(x, y)) \right ] + \mathbb {E}_{z \sim p(z)} \left [ \max (0, 1 + D(G(z, y), y)) \right ] \\ \mathcal {L}_G &= - \mathbb {E}_{z \sim p(z)} \left [ D(G(z, y), y) \right ] \end {aligned} \]
Intuition:
- The discriminator learns to assign a positive score (ideally \(\geq 1\)) to real images \((x, y)\), and a negative score (ideally \(\leq -1\)) to generated images \(G(z, y)\).
- If a sample is already on the correct side of the margin (e.g., a real image with \(D(x, y) > 1\)), the loss is zero — no gradient is applied.
- The generator is trained to maximize the discriminator’s score for its outputs (i.e., make fake images look real to the discriminator).
Why hinge loss helps
- Avoids vanishing gradients when the discriminator becomes too confident (a problem with \(-\log (1 - D(G(z)))\) in early GANs).
- Simplifies optimization with piecewise-linear objectives.
- Empirically improves convergence speed and stability, particularly when combined with spectral normalization.
- Stable Training: With a 1-Lipschitz constraint, the discriminator avoids extreme gradients; the generator receives more reliable updates.
- No Extra Gradient Penalties: Unlike methods (e.g., WGAN-GP) that add penalty terms, SN modifies weights directly, incurring lower overhead.
- Enhanced Diversity: By preventing the discriminator from collapsing too fast, SN often yields more diverse generated samples and mitigates mode collapse.
In practice, Spectral Normalization integrates neatly with standard deep learning frameworks, requiring minimal changes to existing layers. It has become a mainstay technique for reliably training high-quality GANs, used in both unconditional and conditional setups.
Enrichment 20.7.3: Self-Attention GANs (SAGAN)
While convolutional GANs operate effectively on local patterns, they struggle with modeling long-range dependencies, especially in complex scenes. In standard convolutions, each output pixel is influenced only by a small neighborhood of input pixels, and even deep networks require many layers to connect distant features. This becomes problematic in global structure modeling — e.g., maintaining symmetry across a face or coherence across distant body parts.
Self-Attention GANs (SAGAN) [763] address this limitation by integrating non-local self-attention layers into both the generator and discriminator. This allows the model to reason about all spatial locations simultaneously, capturing long-range dependencies without requiring deep, inefficient convolutional hierarchies.
Architecture Overview The self-attention block follows the ”query–key–value” formulation:
- Given an input feature map \( X \in \mathbb {R}^{C \times H \times W} \), three \( 1 \times 1 \) convolutions produce: \( f(X) \) (queries), \( g(X) \) (keys), and \( h(X) \) (values).
- Queries and keys are reshaped to \( C' \times N \) (with \( N = H \cdot W \)) and multiplied, yielding a \( N \times N \) attention map.
- A softmax ensures attention scores sum to 1 across each row (normalized over keys).
- The result is multiplied with values \( h(X) \) and reshaped back to the spatial layout.
- A learnable scale parameter \( \gamma \), initialized to zero, controls the strength of the attention output: \( \mbox{Output} = \gamma \cdot \mbox{SelfAttention}(X) + X \).
- Facilitates global reasoning — e.g., the left eye can align symmetrically with the right, even if they are spatially far apart.
- Improves texture consistency and fine-grained detail preservation in images.
- Enhances expressiveness in multi-class generation tasks like ImageNet.
Training Details and Stabilization SAGAN adopts two key techniques for stable training:
- 1.
- Spectral Normalization [438] applied to both generator and discriminator (unlike earlier approaches which only normalized the discriminator). This constrains each layer’s Lipschitz constant, preventing exploding gradients and improving convergence.
- 2.
- Two Time-Scale Update Rule (TTUR): The generator and discriminator are updated with separate learning rates. This allows the discriminator to stabilize quickly while the generator catches up.
Their combination leads to faster convergence, improved stability, and better FID/IS scores.
Loss Function SAGAN uses the hinge version of the adversarial loss: \[ \mathcal {L}_D = \mathbb {E}_{x \sim p_{\mbox{data}}}[\max (0, 1 - D(x))] + \mathbb {E}_{z \sim p(z)}[\max (0, 1 + D(G(z)))] \] \[ \mathcal {L}_G = - \mathbb {E}_{z \sim p(z)}[D(G(z))] \] This formulation improves gradient behavior by clearly separating the penalties for incorrect real/fake classification.
Quantitative Results SAGAN significantly improves generative performance:
- Achieves state-of-the-art FID and IS scores on ImageNet (128×128).
- Produces semantically consistent outputs, outperforming convolution-only GANs especially on complex classes like “dog” or “person”.
Summary Self-attention enables the generator and discriminator to capture global structures efficiently, helping GANs go beyond local textures. This innovation inspired later models like BigGAN [52], which combine attention, large-scale training, and class conditioning to achieve unprecedented photorealism.
Enrichment 20.7.4: BigGANs: Scaling Up GANs
BigGAN [52] marks a major milestone in the progression of class-conditional GANs by demonstrating that simply scaling up the model and training setup—when coupled with key stabilization techniques—yields state-of-the-art performance across resolution, sample fidelity, and class diversity. Developed by Brock et al., BigGAN pushes the frontier of GAN-based image synthesis, particularly on challenging datasets like ImageNet and JFT-300M.
Key Innovations and Techniques
- Conditional Batch Normalization (CBN): Class labels are incorporated deep into the generator via Conditional BatchNorm layers. Each BatchNorm is modulated by gain and bias vectors derived from a shared class embedding, enabling class-conditional feature modulation.
- Projection-Based Discriminator: The discriminator uses projection [438] to incorporate class information, effectively learning to assess whether an image is both real and aligned with its target class.
- Spectral Normalization (SN): Applied to both \( G \) and \( D \), SN constrains the Lipschitz constant of each layer, enhancing training stability by regularizing weight scales.
- Large-Scale Batch Training: Batch sizes as large as 2048 are used, significantly improving gradient quality and enabling more stable optimization trajectories. Larger batches cover more modes and support smoother convergence.
- Skip-\( z \) Connections: Latent vectors are not only injected at the generator input but also directly routed to multiple residual blocks at various resolutions. These skip connections facilitate hierarchical control over spatial features.
- Residual Architecture: Deep residual blocks enhance gradient flow and feature reuse. BigGAN-deep further expands the architecture using bottleneck ResBlocks and additional layers per resolution.
- Orthogonal Regularization: To support the truncation trick, orthogonal regularization [55] ensures the generator’s mapping from latent space is smooth and well-conditioned. This regularization minimizes cosine similarity between filters while avoiding norm constraints.
- Truncation Trick: During inference, samples are drawn from a truncated normal distribution, i.e., \( z \sim \mathcal {N}(0, I) \) with resampling of values exceeding a fixed magnitude threshold. This concentrates latent inputs around the distribution’s mode, improving visual fidelity at the cost of diversity. The truncation threshold serves as a dial for post-hoc control over the quality–variety tradeoff.
- Exponential Moving Average (EMA): The generator weights are averaged across training steps using an EMA with a decay of 0.9999, improving the quality and consistency of generated samples during evaluation.
- Orthogonal Initialization: All layers in \( G \) and \( D \) are initialized with orthogonal matrices [552], promoting stable signal propagation in very deep networks.
- Hinge Loss and Self-Attention: The architecture adopts hinge loss for adversarial training and includes self-attention modules [763] to improve long-range dependency modeling, especially in higher-resolution images.
Beyond the primary components discussed in earlier parts of this lecture such as label conditioning, spectral normalization, and self-attention—BigGAN incorporates several additional architectural and training innovations that play a crucial role in achieving high-fidelity, scalable synthesis. In what follows, we elaborate on these techniques, mainly those which were not previously covered in depth.
Enrichment 20.7.4.1: Skip-\( z \) Connections: Hierarchical Latent Injection
In conventional conditional GANs, the latent code \( z \in \mathbb {R}^{d} \) is typically introduced at the generator’s input layer and optionally used to initialize class-conditional batch normalization (CBN) in a uniform way. However, this limits the model’s ability to control spatially localized features in a deep generator architecture.
BigGAN implements a refined variant of latent conditioning, referred to as skip-\( z \) connections. The latent vector \( z \) is evenly split into \( L \) chunks—each assigned to one of the generator’s \( L \) residual blocks. Each block uses its assigned chunk \( z_\ell \in \mathbb {R}^{d/L} \) in combination with the shared class embedding \( c \in \mathbb {R}^{d_c} \) to compute block-specific conditional normalization parameters.
- 1.
- Concatenate \( z_\ell \) with \( c \).
- 2.
- Project this vector using two linear layers to produce the gain and bias for CBN.
- 3.
- Apply those to modulate the BatchNorm activations within the residual block.
This process occurs twice per block (once for each BatchNorm layer), and is implemented via reusable layers inside each residual block.
# From BigGAN-PyTorch: ConditionalBatchNorm2d
class ConditionalBatchNorm2d(nn.Module):
def __init__(self, num_features, cond_dim):
super().__init__()
self.bn = nn.BatchNorm2d(num_features, affine=False)
self.gain = nn.Linear(cond_dim, num_features)
self.bias = nn.Linear(cond_dim, num_features)
def forward(self, x, y): # y = [z_chunk, class_embedding]
out = self.bn(x)
gamma = self.gain(y).unsqueeze(2).unsqueeze(3)
beta = self.bias(y).unsqueeze(2).unsqueeze(3)
return gamma * out + betaEach residual block in the generator stores its own ‘ConditionalBatchNorm2d‘ instances and receives its dedicated chunk of \( z \). This allows each layer to capture different aspects of semantic control—for example, coarse structures at lower resolution, textures and edges at higher ones.
Comparison to Standard CBN: In standard conditional normalization, the generator is conditioned on a single global class embedding \( c \), which is reused across all layers. This provides semantic conditioning but lacks spatial specificity. In BigGAN, the class embedding \( c \) remains global and shared, but the latent vector \( z \) is partitioned into chunks \( z^{(l)} \), one per generator block. Each chunk influences a different spatial resolution by being fed into that block’s conditional batch normalization (CBN) layer.
This design allows different parts of the latent code to control different levels of the image hierarchy — from coarse global structure to fine-grained texture. As a result, the generator gains more expressive power and learns a hierarchical organization of semantic and stylistic attributes without modifying the way \( c \) is handled.
BigGAN-deep Simplification: In BigGAN-deep, the latent vector \( z \) is not split. Instead, the full \( z \) vector is concatenated with the class embedding and injected identically into every residual block. While this sacrifices per-layer specialization of \( z \), it simplifies parameter management and works effectively in deeper, bottlenecked architectures.
Enrichment 20.7.4.2: Residual Architecture: Deep and Stable Generators
A cornerstone of BigGAN’s scalability is its reliance on deep residual networks in both the generator and discriminator. Inspired by ResNet-style design [206], BigGAN structures its generator using stacked residual blocks, each of which learns a refinement over its input, enabling stable and expressive function approximation even at hundreds of layers.
Motivation and Design: GAN training becomes increasingly unstable as model capacity grows. Residual blocks counteract this by providing shortcut (identity) connections that facilitate gradient propagation and feature reuse. Each residual block contains:
- Two \( 3 \times 3 \) convolutions (optionally bottlenecked).
- Two conditional batch normalization layers (CBN), conditioned via skip-\( z \) as described earlier.
- A ReLU activation before each convolution.
- A learned skip connection (via \(1\times 1\) conv) when input/output shapes differ.
This design supports deep, expressive generators that do not suffer from vanishing gradients.
BigGAN vs. BigGAN-deep: BigGAN uses relatively shallow residual blocks with a single block per resolution stage. In contrast, BigGAN-deep significantly increases network depth by introducing:
- Two residual blocks per resolution (instead of one).
- Bottlenecked residual layers: each block includes \(1 \times 1\) convolutions before and after the main \(3 \times 3\) convolution to reduce and restore the channel dimensionality.
- Identity-preserving skip connections: in the generator, excess channels are dropped to match dimensions, while in the discriminator, missing channels are padded via concatenation.
These architectural changes enable deeper networks with better training stability and more efficient parameter usage.
These deeper and more modular residual structures help BigGAN-deep outperform its shallower predecessor across all resolutions and evaluation metrics (e.g., FID and IS), while often using fewer parameters due to the bottlenecked design.
Enrichment 20.7.4.3: Truncation Trick in BigGAN: Quality vs. Diversity
The truncation trick is a sampling technique introduced in BigGAN [52] to improve image quality during inference. It restricts latent vectors to lie within a high-density region of the standard normal distribution, where the generator is more likely to produce stable and realistic outputs.
Truncated Normal Distributions in Latent Space During training, the latent code \( z \in \mathbb {R}^d \) is drawn from a standard normal distribution, \( z_i \sim \mathcal {N}(0, 1) \). At test time, the truncation trick samples each component from the same distribution but only accepts values within an interval \( [-\tau , \tau ] \). Formally: \[ z_i \sim \mathcal {N}(0, 1) \quad \mbox{conditioned on} \quad |z_i| \leq \tau \] Samples exceeding \( \tau \) are rejected and resampled. This results in a truncated normal distribution with increased density near the origin and zero probability beyond the cutoff. The distribution is renormalized so that it still integrates to 1.
Why Truncate? In high-dimensional Gaussian space, most probability mass is concentrated in a thin spherical shell around \( \|z\|_2 \approx \sqrt {d} \). These high-norm vectors are often mapped by the generator to unstable or low-quality outputs. Truncation focuses sampling on lower-norm vectors near the origin—regions where the generator has been well-trained. This leads to:
- Cleaner and sharper images.
- Reduced artifacts.
- Stronger alignment with class-conditional structure.
How Is \( \tau \) Chosen? The truncation threshold \( \tau \) is a tunable hyperparameter. Smaller values yield higher quality but reduce diversity. Common values include \( \tau = 2.0 \), \( 1.5 \), \( 1.0 \), or \( 0.5 \). In practice, a truncation sweep is performed to empirically select the best trade-off. BigGAN reports IS and FID for multiple truncation levels, revealing the tradeoff curve between sample quality and variety.
Implementation in Practice Truncated sampling is implemented via per-dimension rejection sampling:
from scipy.stats import truncnorm
def truncated_z(dim, tau):
return truncnorm.rvs(-tau, tau, loc=0, scale=1, size=dim)This procedure generates a latent vector \( z \in \mathbb {R}^d \) with each component sampled independently from \( \mathcal {N}(0, 1) \), truncated to \( [-\tau , \tau ] \).
Tradeoffs and Limitations Truncation improves sample fidelity but comes with costs:
- Reduced Diversity: A smaller volume of latent space is explored.
- Possible Instability: Generators not trained to handle low-norm regions may produce collapsed or saturated outputs.
When Truncation Fails If the generator lacks smoothness near \( z = 0 \), truncation can trigger saturation artifacts or mode collapse. This happens when the model overfits to high-norm training inputs and generalizes poorly to low-norm regions. Thus, truncation should be used only with generators that have been explicitly regularized for this purpose.
How to Make Truncation Work Reliably To ensure that the generator behaves well under truncation, BigGAN applies orthogonal regularization, which promotes smoothness and local isometry in the latent-to-image mapping. This regularization term discourages filter redundancy and ensures the generator responds predictably to small latent variations—especially those near the origin.
Enrichment 20.7.4.4: Orthogonal Regularization: A Smoothness Prior for Truncated Latents
Orthogonal regularization is a key technique introduced in BigGAN to ensure that the generator remains well-behaved in low-norm regions of latent space—regions emphasized by the truncation trick. While truncation improves sample quality by concentrating latent inputs near the origin, this strategy only works reliably if the generator maps these inputs smoothly and predictably to images. Without this property, truncation may lead to artifacts, over-saturation, or even complete mode collapse.
To address this, BigGAN introduces a soft form of orthogonality constraint on the generator’s weight matrices. The goal is to encourage the columns of each weight matrix to be approximately orthogonal to each other. This makes each layer in the generator act as a near-isometric transformation, where similar inputs lead to similar outputs. As a result, local neighborhoods in latent space map to locally coherent image regions.
The standard orthogonal regularization term penalizes deviations from strict orthogonality by minimizing the squared Frobenius norm of the off-diagonal entries in \( W^\top W \), where \( W \) is a weight matrix: \[ \mathcal {L}_{\mbox{ortho}} = \lambda \left \| W^\top W - I \right \|_F^2 \] However, in practice, this constraint is too strong and can limit model expressiveness. Instead, BigGAN uses a relaxed variant that excludes the diagonal entries, focusing only on reducing correlations between filters while allowing their norms to vary. The regularization term becomes: \[ \mathcal {L}_{\mbox{ortho}} = \lambda \left \| W^\top W \odot (1 - I) \right \|_F^2 \] where \( I \) is the identity matrix and \( \odot \) denotes element-wise multiplication. This version of the penalty preserves the desired smoothness properties without overly constraining the generator’s capacity.
Empirical results show that orthogonal regularization dramatically increases the likelihood that a generator will remain stable under truncated sampling. In the BigGAN paper, only 16% of large models were truncation-tolerant without orthogonal regularization.
When this penalty was included, the success rate increased to over 60%. These results confirm that enforcing orthogonality improves the conditioning of the generator and mitigates gradient pathologies that would otherwise arise in narrow latent regions.
In implementation, orthogonal regularization is applied as an auxiliary term added to the generator’s loss during training. It is computed across all linear and convolutional weight matrices using simple matrix operations. Its computational overhead is negligible compared to the benefits it provides in stability, generalization, and quality at inference time—particularly when truncated latent vectors are used.
Orthogonal regularization should not be confused with orthogonal initialization, although both arise from the same geometric motivation: preserving distance and structure through linear transformations. Orthogonal initialization sets the initial weights of a neural network to be orthogonal matrices, satisfying \( W^\top W = I \) at initialization time. This technique was introduced in the context of deep linear and recurrent networks [552] to maintain variance propagation and avoid gradient explosion or vanishing.
BigGAN applies orthogonal initialization to all convolutional and linear layers in both the generator and the discriminator. This initialization ensures that the model starts in a well-conditioned regime where activations and gradients are stable across many layers. However, during training, weight matrices are updated by gradient descent and quickly deviate from orthogonality. This is where orthogonal regularization becomes essential—it continuously nudges the model back toward this structured regime.
Thus, orthogonal initialization provides a favorable starting point, while orthogonal regularization acts as a guiding prior during optimization. Their combination is especially effective in large-scale GANs: initialization alone may be insufficient to prevent pathological gradients, and regularization alone may be ineffective if starting from arbitrary weights. Together, they enable BigGAN to maintain spatial smoothness and local isometry throughout training, which is critical for its ability to support low-norm latent vectors and reliably generate high-quality images under truncation.
Enrichment 20.7.4.5: Exponential Moving Average (EMA) of Generator Weights
Another subtle but powerful technique used in BigGAN is the application of an exponential moving average (EMA) over the generator weights during training. Although it does not influence the optimization process directly, EMA plays a critical role during evaluation and sample generation. It acts as a temporal smoothing mechanism over the generator’s parameter trajectory, helping to counteract the noise and instability of high-variance gradient updates that occur throughout adversarial training.
The EMA maintains a running average of the generator’s weights \( \theta _t \) according to the update rule: \[ \theta ^{\mbox{EMA}}_t = \alpha \cdot \theta ^{\mbox{EMA}}_{t-1} + (1 - \alpha ) \cdot \theta _t \] where \( \alpha \in (0, 1) \) is the decay rate, often set very close to 1 (e.g., \( \alpha = 0.999 \) or \( 0.9999 \)). This formulation gives exponentially more weight to recent updates while slowly fading out older values. As training progresses, the EMA model tracks the moving average of each parameter across steps, effectively producing a smoothed version of the generator that is less affected by momentary oscillations or adversarial instability.
In practice, EMA is not used during training updates or backpropagation. Instead, a shadow copy of the generator is maintained and updated using the EMA formula after each optimization step.
Then, when it comes time to evaluate the generator—either for computing metrics like Inception Score or FID, or for sampling images for qualitative inspection—BigGAN uses this EMA-smoothed generator instead of the raw, most-recent checkpoint.
The benefits of this approach are particularly visible in high-resolution settings, where adversarial training can produce noisy or unstable weight fluctuations even when the model as a whole is converging. The EMA model filters out these fluctuations, resulting in visibly cleaner and more coherent outputs. It also improves quantitative metrics across the board, with lower FID scores and reduced sample variance across random seeds.
The idea of averaging model parameters over time is not unique to GANs—it has a long history in convex optimization and stochastic learning theory, and is closely related to Polyak averaging. However, in the context of GANs, it gains particular significance due to the non-stationary nature of the loss surface and the adversarial updates. The generator is not optimizing a static objective but is instead constantly adapting to a co-evolving discriminator. EMA helps decouple the generator from this shifting target by producing a more stable parameter estimate over time.
It is also worth noting that EMA becomes increasingly important as model size and capacity grow. In very large generators, even small perturbations to weight matrices can lead to visible differences in output. This sensitivity is amplified when using techniques like truncation sampling, which further constrain the input space. The EMA generator mitigates these issues by producing a version of the model that is representative of the broader training trajectory, rather than any single volatile moment in optimization.
In BigGAN, the EMA weights are typically stored alongside the training weights, and a final evaluation pass is conducted exclusively using the averaged version. This ensures that reported metrics reflect the most stable version of the model. As a result, EMA has become a de facto standard in high-quality GAN implementations, extending well beyond BigGAN into diffusion models, VAEs, and other generative frameworks that benefit from stable parameter averaging.
Enrichment 20.7.4.6: Discriminator-to-Generator Update Ratio
A key practical detail in BigGAN’s training strategy is its use of an asymmetric update schedule between the generator and discriminator. Specifically, for every generator update, the discriminator is updated twice. This 2:1 update ratio, while simple, has a significant impact on training stability and convergence—particularly during early stages when the generator is still producing low-quality outputs and lacks meaningful gradients.
This design choice arises from the fundamental nature of GANs as a two-player minimax game rather than a supervised learning problem. In the standard GAN objective, the generator relies on the discriminator to provide gradients that guide it toward producing more realistic samples. If the discriminator is undertrained or inaccurate, it fails to deliver informative gradients. In such cases, the generator may either receive gradients with very low magnitude (i.e., saturated) or gradients that are inconsistent and directionless. Either scenario leads to unstable training, poor convergence, or mode collapse.
Updating the discriminator more frequently ensures that it can closely track the current distribution of fake samples produced by the generator. In early training, this is especially important: the generator often outputs near-random images, while the discriminator can quickly learn to distinguish these from real samples. However, the generator can only learn effectively if the discriminator provides non-saturated gradients—responses that are confident yet not flat. By giving the discriminator extra updates, the model maintains a discriminator that is sufficiently strong to provide meaningful feedback but not so dominant that it collapses the generator.
This update schedule also compensates for the relatively high gradient variance and weaker signal that the generator typically receives. Since the generator’s loss depends entirely on how the discriminator scores its outputs, and because these outputs change with each batch, the gradient landscape faced by the generator is inherently less stable. Additional discriminator updates help mitigate this instability by ensuring that the discriminator has time to adapt to the generator’s latest distribution before a new generator step is taken.
Importantly, this strategy only works in combination with proper regularization. BigGAN uses spectral normalization in both \( G \) and \( D \) to constrain the discriminator’s Lipschitz constant and prevent overfitting. Without such constraints, training the discriminator more aggressively could lead it to perfectly memorize the training data or overpower the generator entirely, resulting in vanishing gradients.
While BigGAN settles on a 2:1 update ratio, other GAN variants may use different values depending on model complexity and the chosen loss function. For example, WGAN-GP updates the discriminator five times for every generator update to approximate the Wasserstein distance reliably. In contrast, StyleGAN2-ADA uses a 1:1 schedule but includes strong regularization and adaptive data augmentation to stabilize training. Ultimately, the ideal update frequency is a function of architectural depth, dataset difficulty, and the adversarial loss landscape. In BigGAN’s case, the 2:1 ratio is a well-calibrated compromise that supports rapid discriminator adaptation without overwhelming the generator.
Results and Legacy Trained on ImageNet, BigGAN models achieved an Inception Score (IS) of 166.5 and FID of 7.4 at \(128\times 128\) resolution—substantially surpassing previous benchmarks. The models generalize well to larger datasets such as JFT-300M and have inspired a cascade of follow-up works, including:
- BigBiGAN [130], which extends BigGAN with an encoder network, enabling bidirectional mapping and representation learning;
- ADM-G [123], whose strong results in class-conditional image synthesis with diffusion models were, in part, motivated by BigGAN’s performance ceiling;
- StyleGAN-T [321], a transformer-based GAN combining BigGAN-style residual backbones with Vision Transformer decoders;
- Consistency Models [581], which revisit training efficiency, stability, and realism tradeoffs using simplified objectives beyond GANs.
These extensions signal BigGAN’s long-standing impact—not merely as a powerful model, but as a catalyst for the generative modeling community’s move toward scalable, stable, and controllable synthesis. Its emphasis on architectural regularization, batch scaling, and sample quality–diversity tradeoffs continues to shape SOTA pipelines.
Enrichment 20.7.5: StackGAN: Two-Stage Text-to-Image Synthesis
StackGAN [765] introduced a pivotal advancement in text-to-image generation by proposing a two-stage architecture that decomposes the synthesis process into coarse sketching and progressive refinement. This design is inspired by how human artists typically work: first sketching global structure, then layering fine-grained detail. The central insight is that generating high-resolution, photorealistic images directly from text is extremely difficult—both because modeling fine detail in a single forward pass is computationally unstable, and because the generator must preserve semantic alignment with the conditioning text at increasing resolutions.
Earlier works such as GAN-INT-CLS [519] and GAWWN [520] introduced conditional GANs based on text embeddings. GAN-INT-CLS used a pre-trained RNN to encode descriptive captions into fixed-size vectors, which were then concatenated with noise and passed through a generator to produce \(64 \times 64\) images. While conceptually sound, it failed to capture high-frequency details or generate sharp textures. GAWWN added spatial attention and object location hints, but similarly struggled at scaling beyond low resolutions or preserving semantic richness.
StackGAN addresses these challenges by introducing a two-stage generator pipeline. But before either stage operates, StackGAN applies a crucial transformation called Conditioning Augmentation (CA). Instead of feeding the text embedding \( \phi _t \in \mathbb {R}^D \) directly into the generator, CA maps it to a Gaussian distribution \( \mathcal {N}(\mu (\phi _t), \Sigma (\phi _t)) \) using a learned mean and diagonal covariance. A conditioning vector \( \hat {c} \sim \mathcal {N}(\mu , \Sigma ) \) is then sampled and used as the actual conditioning input.
This stochastic perturbation serves several purposes:
- It encourages smoothness in the conditioning manifold, making the generator less brittle to small changes in text.
- It introduces variation during training, acting like a regularizer that improves generalization.
- It helps overcome mode collapse by encouraging the generator to explore nearby conditioning space without drifting far from the intended semantics.
With CA in place, StackGAN proceeds in two stages:
- Stage-I Generator: Takes as input the sampled conditioning vector \( \hat {c} \) and a random noise vector \( z \), and synthesizes a coarse \(64 \times 64\) image. This image captures the global layout, color palette, and rough object geometry implied by the text. However, it typically lacks sharpness and fine-grained texture.
- Stage-II Generator: Refines the low-resolution image by conditioning again on the original text embedding (not the sampled \( \hat {c} \)) and the Stage-I output. It corrects distortions, enhances object boundaries, and synthesizes photorealistic detail. This generator is built as a residual encoder–decoder network, with upsampling layers and deep residual connections that allow semantic feature reuse. The discriminator in this stage is also enhanced with matching-aware supervision to ensure image–text consistency.
The effect of this staged generation is illustrated in Figure 20.45. While one-stage GANs struggle to produce realistic \(256 \times 256\) images—even when equipped with deep upsampling layers—StackGAN’s sketch-and-refine paradigm achieves significantly better visual fidelity. Stage-I outputs provide rough structure, and Stage-II convincingly improves resolution, texture, and alignment with text cues.
The architectural overview illustrates the interaction between text embeddings, conditioning augmentation, and residual refinement. The text embedding is used at both stages to ensure that conditioning information is not lost in early transformations. Residual blocks in Stage-II integrate features from both the coarse image and the original text to construct plausible details aligned with the semantics of the prompt.
This two-stage framework offers several advantages:
- It decomposes the generation task into manageable subgoals: layout and detail.
- It maintains semantic consistency by conditioning both stages on the text.
- It improves training stability and image diversity through CA.
From Overview to Components: We now examine each of StackGAN’s core components in detail. The entire system is built on a simple but powerful idea: rather than attempting to generate high-resolution images in a single step, StackGAN decomposes the process into well-defined stages. Each stage plays a specialized role in the pipeline, and the quality of the final output hinges critically on the strength of the conditioning mechanism that feeds it.
We begin by studying Conditioning Augmentation (CA), which precedes both Stage-I and Stage-II generators and provides the stochastic conditioning vector from which the entire synthesis process unfolds. This module acts as the semantic foundation of StackGAN, and understanding it will clarify how subsequent stages achieve stability, diversity, and realism.
Enrichment 20.7.5.1: Conditioning Augmentation (CA)
A central challenge in text-conditioned GANs is that each natural language caption is mapped to a fixed high-dimensional embedding vector \( \phi _t \in \mathbb {R}^D \), typically obtained via an RNN-based text encoder. While these embeddings successfully encode semantics, they pose three major problems for image generation:
- Determinism: A single text embedding maps to a single point in feature space, limiting image diversity for the same caption.
- Sparsity and Interpolation Gaps: Fixed embeddings lie on a sparse, irregular manifold, making interpolation and smooth generalization difficult.
- Overfitting: The generator may memorize how to map a specific caption embedding to a specific image, risking mode collapse.
Solution: Learn a Distribution Over Conditioning Vectors StackGAN addresses these issues with Conditioning Augmentation (CA), which models a distribution over conditioning vectors rather than using a single deterministic embedding. Given a text embedding \( \phi _t \), CA learns the parameters of a Gaussian distribution: \[ \hat {c} \sim \mathcal {N}\left ( \mu (\phi _t), \operatorname {diag}(\sigma ^2(\phi _t)) \right ) \] where \( \mu (\phi _t) \in \mathbb {R}^{N_g} \) and \( \log \sigma ^2(\phi _t) \in \mathbb {R}^{N_g} \) are the outputs of two fully connected layers applied to \( \phi _t \). This distribution introduces controlled randomness into the conditioning process.
Sampling via Reparameterization Trick To ensure end-to-end differentiability, CA uses the reparameterization trick—first introduced in variational autoencoders: \[ \hat {c} = \mu (\phi _t) + \sigma (\phi _t) \odot \epsilon , \qquad \epsilon \sim \mathcal {N}(0, I) \] where \( \hat {c} \in \mathbb {R}^{N_g} \) becomes the actual conditioning input for the generator, and \( \odot \) denotes elementwise multiplication. This trick enables gradients to propagate through the stochastic sampling process during training.
KL Divergence Regularization To avoid arbitrary shifts in the learned distribution and ensure it remains centered and stable, CA includes a regularization term: \[ \mathcal {L}_{\mathrm {KL}} = D_{\mathrm {KL}}\left ( \mathcal {N}(\mu (\phi _t), \operatorname {diag}(\sigma ^2(\phi _t))) \;\|\; \mathcal {N}(0, I) \right ) \] This KL divergence penalizes deviations from the standard normal distribution, thereby encouraging the learned \( \mu \) to stay near zero and \( \sigma \) near one. This regularization discourages degenerate behavior such as collapsing the variance to zero (making CA deterministic again). The KL loss is added to the generator’s total loss during training.
Benefits of Conditioning Augmentation
- Diversity from Fixed Input: Sampling \( \hat {c} \) from a learned Gaussian allows multiple plausible images to be generated from a single caption \( \phi _t \).
- Smooth Latent Manifold: The conditioning space becomes more continuous, improving interpolation, generalization, and gradient flow.
- Robustness and Regularization: The KL penalty prevents the conditioning distribution from drifting arbitrarily far from the origin, which stabilizes training.
Summary Table: Conditioning Augmentation
| Component | Role |
|---|---|
| \( \phi _t \) | Sentence embedding from text encoder |
| \( \mu (\phi _t), \sigma ^2(\phi _t) \) | Parameters of a diagonal Gaussian |
| \( \hat {c} \) | Sampled conditioning vector fed to the generator |
| \( \mathcal {L}_{\mathrm {KL}} \) | Regularizer to keep \( \mathcal {N}(\mu , \sigma ^2) \) close to \( \mathcal {N}(0, I) \) |
Having established a robust and diverse conditioning vector \( \hat {c} \) via CA, we now turn to the first stage of generation: a low-resolution GAN that translates this semantic vector into a coarse but globally coherent image layout.
Enrichment 20.7.5.2: Stage-I Generator: Coarse Sketching from Noise and Caption
After sampling a stochastic conditioning vector \( \hat {c} \in \mathbb {R}^{N_g} \) via Conditioning Augmentation (CA), the Stage-I generator synthesizes a coarse \( 64 \times 64 \) image that captures the global layout, dominant colors, and rough object shapes. This stage is intentionally lightweight, focusing not on photorealism, but on producing a semantically plausible sketch aligned with the text description.
Motivation: Why Two Stages? Generating high-resolution images (e.g., \(256 \times 256\)) directly from noise and text is challenging due to multiple factors:
- Gradient instability: GAN training at large resolutions often suffers from unstable optimization.
- Complex mappings: A direct mapping from \( (z, \phi _t) \mapsto \mbox{image} \) must simultaneously learn global structure and fine-grained detail.
- Mode collapse: High-resolution generation without strong inductive structure can lead to poor sample diversity or overfitting.
To mitigate these issues, StackGAN breaks the synthesis process into two distinct tasks:
- Stage-I: Learn to generate a coarse image from the conditioning vector.
- Stage-II: Refine that image into a high-fidelity result using residual enhancement.
This decomposition improves modularity, training stability, and sample quality, following the same coarse-to-fine approach used in human drawing.
Architecture of Stage-I Generator The generator takes as input: \[ z \sim \mathcal {N}(0, I), \qquad \hat {c} \sim \mathcal {N}(\mu (\phi _t), \sigma ^2(\phi _t)) \] where \( z \in \mathbb {R}^{N_z} \) is a standard Gaussian noise vector and \( \hat {c} \in \mathbb {R}^{N_g} \) is the sampled conditioning vector. These vectors are concatenated to form a combined input: \[ h_0 = [z; \hat {c}] \in \mathbb {R}^{N_z + N_g} \]
The forward pass proceeds as follows:
- 1.
- Fully connected layer: \( h_0 \) is mapped to a dense feature vector and reshaped to a spatial tensor (e.g., \( 4 \times 4 \times 512 \)).
- 2.
- Upsampling blocks: A series of convolutional blocks upsample this tensor
progressively to \(64 \times 64\), each consisting of:
- Nearest-neighbor upsampling (scale factor 2)
- \(3 \times 3\) convolution to reduce channel dimensionality
- Batch Normalization
- ReLU activation
- 3.
- Final layer: A \(3 \times 3\) convolution maps the output to 3 channels (RGB), followed by a Tanh activation: \[ I_{\mbox{stage-I}} = \tanh (\mbox{Conv}_{\mbox{RGB}}(h)) \in \mathbb {R}^{64 \times 64 \times 3} \]
Output Normalization: Why Tanh? The Tanh function ensures that pixel values lie in the range \( (-1, 1) \). This matches the normalized data distribution used during training and avoids vanishing gradients more effectively than the Sigmoid function, which squashes values into \( [0, 1] \) and saturates near boundaries. Moreover, Tanh is zero-centered, which harmonizes well with BatchNorm layers that follow a zero-mean distribution.
From Latent Tensor to Displayable Image At inference time, the generated image \( I \in [-1, 1]^{H \times W \times 3} \) is rescaled to displayable RGB format via: \[ \mbox{image}_{\mbox{uint8}} = \left ( \frac {I + 1}{2} \right ) \times 255 \] This rescaling is not part of the generator architecture—it is applied externally during image saving or visualization.
How Channel Reduction Works in Upsampling Blocks A common misconception is that upsampling reduces the number of channels. In fact:
- Upsampling (e.g., nearest-neighbor or bilinear) increases spatial resolution, but preserves channel depth.
- Convolution that follows upsampling reduces channel dimensionality via learned filters.
Thus, a typical stack in Stage-I looks like: \[ \begin {aligned} 4 \times 4 \times 512 &\rightarrow 8 \times 8 \times 256 \\ &\rightarrow 16 \times 16 \times 128 \\ &\rightarrow 32 \times 32 \times 64 \\ &\rightarrow 64 \times 64 \times 3 \end {aligned} \] Each transition consists of: upsample → convolution → BatchNorm → ReLU.
| Component | Role |
|---|---|
| \( z \sim \mathcal {N}(0, I) \) | Random noise to seed diversity |
| \( \hat {c} \sim \mathcal {N}(\mu , \sigma ^2) \) | Conditioning vector from CA |
| FC layer | Projects input into spatial feature map |
| Upsampling + Conv blocks | Build image resolution step-by-step |
| Final Tanh activation | Constrains pixel values to \( [-1, 1] \) |
This completes the first stage of StackGAN. The output image \( I_{\mbox{stage-I}} \) serves as a rough semantic sketch that is then refined in Stage-II, where texture, edges, and class-specific details are injected in a residual encoder–decoder framework.
Enrichment 20.7.5.3: Stage-II Generator: Refinement with Residual Conditioning
The Stage-I Generator outputs a low-resolution image \( I_{\mbox{stage-I}} \in [-1, 1]^{64 \times 64 \times 3} \) that captures the coarse spatial layout and color distribution of the target object. However, it lacks photorealistic texture and fine-grained semantic details. To address this, StackGAN introduces a Stage-II Generator that refines \( I_{\mbox{stage-I}} \) into a high-resolution image (typically \(256 \times 256\)) by injecting residual information—guided again by the original text description.
Why Two Stages Are Beneficial The division of labor into two stages is not arbitrary. It allows the model to separate:
- Global coherence and layout (handled by Stage-I)
- Local realism, edges, and fine detail (handled by Stage-II)
This decomposition mimics human drawing: a rough sketch is laid down first, then detail is added in successive refinement passes. The result is more stable training, higher sample fidelity, and clearer semantic grounding.
Inputs to Stage-II Generator Stage-II receives: \[ I_{\mbox{stage-I}} \in \mathbb {R}^{64 \times 64 \times 3}, \quad \hat {c} \in \mathbb {R}^{N_g} \] where \( I_{\mbox{stage-I}} \) is the output from Stage-I, and \( \hat {c} \) is the same conditioning vector sampled from the CA module.
Network Structure and Residual Design The Stage-II Generator follows an encoder–decoder architecture with residual connections:
- 1.
- Downsampling encoder: The \(64 \times 64\) image is downsampled through strided convolutions, extracting a hierarchical feature representation.
- 2.
- Text-aware residual blocks: The encoded features are concatenated with the text conditioning vector \( \hat {c} \) and processed through multiple residual blocks: \[ x \mapsto x + F(x, \hat {c}) \] where \( F \) is a learnable function composed of BatchNorm, ReLU, and convolutions, modulated by the text embedding.
- 3.
- Upsampling decoder: The enhanced feature map is upsampled through nearest-neighbor blocks and convolutions until it reaches size \(256 \times 256 \times 3\).
- 4.
- Tanh activation: A final \(3 \times 3\) convolution followed by Tanh ensures output pixel values are in \( [-1, 1] \).
Semantic Reinforcement via Dual Conditioning One subtle but critical detail is that Stage-II does not rely solely on the coarse image. It also reuses the original caption embedding \( \phi _t \) via the CA vector \( \hat {c} \), allowing it to reinterpret the initial sketch and enforce textual alignment. This reinforcement ensures that Stage-II does not merely sharpen the image, but corrects and realigns it to better reflect the input caption.
Discriminator in Stage-II The Stage-II Discriminator is also conditioned on text. It takes as input: \[ D_{\mbox{Stage-II}}(I_{\mbox{fake}}, \phi _t) \] and is trained to distinguish between real and generated images given the caption. It follows a PatchGAN-style architecture and applies spectral normalization to improve convergence.
Overall Effect of Stage-II Compared to naive GANs that attempt high-resolution synthesis in a single pass, StackGAN’s residual refinement strategy in Stage-II enables:
- Sharper object boundaries and fine-grained textures (e.g., feathers, eyes, flower petals)
- Fewer artifacts and better color consistency
- Improved semantic alignment between caption and image
| Component | Role |
|---|---|
| \( I_{\mbox{stage-I}} \in \mathbb {R}^{64 \times 64 \times 3} \) | Coarse layout from Stage-I |
| \( \hat {c} \in \mathbb {R}^{N_g} \) | Conditioning vector from CA (reused) |
| Encoder network | Extracts low-res image features |
| Residual blocks | Refine features using text-aware transformation |
| Decoder network | Upsamples features to \(256 \times 256\) |
| Final Tanh | Outputs image in \( [-1, 1] \) range |
Together with CA and Stage-I, this final refinement stage completes the StackGAN architecture, establishing a blueprint for many follow-up works in text-to-image synthesis that adopt coarse-to-fine generation, residual conditioning, and staged refinement.
Enrichment 20.7.5.4: Training Procedure and Multi-Stage Objectives
StackGAN is trained in two sequential stages, each consisting of its own generator–discriminator pair and loss functions. The Conditioning Augmentation (CA) module is shared and optimized during both stages via an additional KL divergence penalty.
Stage-I Training: The Stage-I generator \( G_0 \) receives noise \( z \sim \mathcal {N}(0, I) \) and a sampled conditioning vector \( \hat {c} \sim \mathcal {N}(\mu (\phi _t), \sigma ^2(\phi _t)) \) from the CA module, and outputs a coarse image \( I_{\mbox{stage-I}} \in \mathbb {R}^{64 \times 64 \times 3} \). A discriminator \( D_0 \) is trained to classify whether this image is real and whether it corresponds to the conditioning text embedding \( \phi _t \). The training losses are:
- Stage-I Discriminator Loss: \[ \mathcal {L}_{D_0} = \mathbb {E}_{(x, \phi _t)}[\log D_0(x, \phi _t)] + \mathbb {E}_{(z, \hat {c})}[\log (1 - D_0(G_0(z, \hat {c}), \phi _t))] \] where \( x \) is a real image and \( G_0(z, \hat {c}) \) is the generated fake image.
- Stage-I Generator Loss: \[ \mathcal {L}_{G_0}^{\mbox{total}} = \mathbb {E}_{(z, \hat {c})}[\log D_0(G_0(z, \hat {c}), \phi _t)] + \lambda _{\mathrm {KL}} \cdot \mathcal {L}_{\mathrm {KL}}^{(0)} \] where the KL divergence term is: \[ \mathcal {L}_{\mathrm {KL}}^{(0)} = D_{\mathrm {KL}}\left ( \mathcal {N}(\mu (\phi _t), \sigma ^2(\phi _t)) \;\|\; \mathcal {N}(0, I) \right ) \]
The generator \( G_0 \) and the CA module are updated together to minimize \( \mathcal {L}_{G_0}^{\mbox{total}} \), while the discriminator \( D_0 \) is trained to minimize \( \mathcal {L}_{D_0} \).
Stage-II Training: After Stage-I has converged, its generator \( G_0 \) is frozen. The Stage-II generator \( G_1 \) takes \( I_{\mbox{stage-I}} \) and a new sample \( \hat {c} \sim \mathcal {N}(\mu (\phi _t), \sigma ^2(\phi _t)) \), and refines the image to high resolution \( I_{\mbox{stage-II}} \in \mathbb {R}^{256 \times 256 \times 3} \). A second discriminator \( D_1 \) is trained to distinguish between real and generated high-resolution images, given the same conditioning text.
- Stage-II Discriminator Loss: \[ \mathcal {L}_{D_1} = \mathbb {E}_{(x, \phi _t)}[\log D_1(x, \phi _t)] + \mathbb {E}_{(\hat {x}, \phi _t)}[\log (1 - D_1(G_1(I_{\mbox{stage-I}}, \hat {c}), \phi _t))] \] where \( x \) is a real \(256 \times 256\) image and \( \hat {x} = G_1(I_{\mbox{stage-I}}, \hat {c}) \) is the generated refinement.
- Stage-II Generator Loss: \[ \mathcal {L}_{G_1}^{\mbox{total}} = \mathbb {E}_{(\hat {x}, \phi _t)}[\log D_1(G_1(I_{\mbox{stage-I}}, \hat {c}), \phi _t)] + \lambda _{\mathrm {KL}} \cdot \mathcal {L}_{\mathrm {KL}}^{(1)} \] with the KL regularization again encouraging the conditioning distribution to remain close to standard normal.
Training Alternation: For each stage, training proceeds by alternating updates between:
- The generator \( G_i \), which minimizes \( \mathcal {L}_{G_i}^{\mbox{total}} \)
- The discriminator \( D_i \), which minimizes \( \mathcal {L}_{D_i} \)
- The CA module (through shared gradients with \( G_i \))
Stage-I and Stage-II are not trained jointly but in sequence. This modular strategy prevents instability, improves sample fidelity, and mirrors a hierarchical refinement process—first capturing scene layout, then enhancing texture and semantic alignment.
Enrichment 20.7.5.5: Legacy and Extensions: StackGAN++ and Beyond
StackGAN’s core contribution is not merely architectural, but conceptual. By recognizing that text-to-image generation is inherently hierarchical, it introduced a modular, interpretable strategy that has since become foundational. Many subsequent works—such as StackGAN++ [766], AttnGAN [715], and DM-GAN [806]—build directly on its key innovations in conditioning augmentation, multi-stage generation, and residual refinement.
StackGAN++ generalizes the two-stage approach of StackGAN into a more flexible and scalable multi-branch architecture. Instead of just two stages, StackGAN++ supports an arbitrary number of generators operating at increasing resolutions (e.g., \(64 \times 64\), \(128 \times 128\), \(256 \times 256\)), all trained jointly in an end-to-end fashion. Unlike StackGAN, where the second stage generator is trained after freezing the first, StackGAN++ employs shared latent features and hierarchical skip connections across all branches—enabling simultaneous refinement of low-to-high resolution details. It also removes explicit Conditioning Augmentation and instead integrates conditional information at each scale using residual connections and shared text embeddings. This makes training more stable and improves semantic alignment across resolutions. Additionally, each generator stage in StackGAN++ has its own dedicated discriminator, enabling finer gradient signals at every level of resolution.
These changes make StackGAN++ more robust to training instabilities and better suited to modern high-resolution synthesis tasks. By enabling joint optimization across scales and conditioning paths, it sets the stage for more sophisticated architectures like AttnGAN, which further introduces word-level attention mechanisms to ground visual details in fine-grained linguistic tokens.
Enrichment 20.7.6: VQ-GAN: Taming Transformers for High-Res Image Synthesis
Enrichment 20.7.6.1: VQ-GAN: Overview and Motivation
VQ-GAN [148] combines the efficient compressive abilities of Vector Quantized Variational Autoencoders (VQ-VAE) with the powerful generative capabilities of transformers. It introduces a hybrid architecture where a convolutional autoencoder compresses images into spatially structured discrete visual tokens, and a transformer models the distribution over these tokens to enable high-resolution synthesis. Unlike VQ-VAE-2 [514], which uses hierarchical convolutional priors for modeling, VQ-GAN incorporates adversarial and perceptual losses during training to enhance visual fidelity and semantic richness in the learned codebook.
This section builds upon the foundation set by VQ-VAE-2 (§20.3.1) and now turns to a detailed examination of the VQ-GAN’s key innovations—beginning with its codebook structure and perceptual training objectives. It is highly suggested to read the VQ-VAE2 part prior continuing if you haven’t done so already.
The design of VQ-GAN addresses a core trade-off in image synthesis: transformers are well-suited to modeling global, compositional structure but are computationally expensive when applied directly to high-resolution pixel grids due to their quadratic scaling. In contrast, convolutional neural networks (CNNs) are highly efficient in processing local image features—such as textures, edges, and short-range patterns—because of their spatial locality and weight-sharing mechanisms. While this practical strength is sometimes referred to as an inductive bias, the term itself is not precisely defined; in this context, it reflects the empirical observation that CNNs excel at capturing local correlations in natural images. However, they often fail to model long-range dependencies without additional architectural support or stacking many layers one after the other, creating very deep and computationally expensive architectures.
VQ-GAN bridges this gap by:
- Using a CNN-based encoder–decoder to transform images into discrete tokens arranged on a spatial grid.
- Employing a transformer to model the autoregressive distribution over these tokens.
The result is a generator that is both efficient and expressive—capable of scaling to resolutions like \( 256 \times 256 \), \( 512 \times 512 \), and beyond. This overall pipeline proceeds in two stages. First, a convolutional encoder maps the image \( x \in \mathbb {R}^{H \times W \times 3} \) into a low-resolution latent feature map \( \hat {z} \in \mathbb {R}^{h \times w \times d} \). Each feature vector \( \hat {z}_{ij} \) is then quantized to its nearest code \( z_k \in \mathcal {Z} = \{z_1, \ldots , z_K\} \) from a learned codebook \( \mathcal {Z} \subset \mathbb {R}^d \). The decoder reconstructs the image \( \hat {x} = G(z_q) \) from this quantized map \( z_q \). Unlike VQ-VAE, which minimizes pixel-level MSE, VQ-GAN uses a combination of perceptual loss \( \mathcal {L}_{\mbox{perc}} \) (measured between VGG features) and a patch-based adversarial loss \( \mathcal {L}_{\mbox{GAN}} \) to enforce both high-level semantic similarity and local realism. These losses enhance the codebook’s ability to capture visually meaningful features.
Once the autoencoder and codebook are trained, they are frozen, and a transformer is trained on the flattened sequence of codebook indices. The goal is to learn the joint distribution: \[ p(s) = \prod _{i=1}^{N} p(s_i \mid s_{<i}) \] where \( s \in \{1, \ldots , K\}^N \) is the raster-scanned sequence of codebook entries for an image. Training proceeds via standard teacher-forced cross-entropy.
At inference time, sampling is performed autoregressively one token at a time. To mitigate the computational cost of modeling long sequences (e.g., 1024 tokens for \(32 \times 32\) maps), VQ-GAN adopts a sliding window self-attention mechanism during sampling, which limits the receptive field at each generation step. This approximation enables tractable synthesis at high resolutions while preserving global structure.
In summary, VQ-GAN decouples local perceptual representation from global autoregressive modeling, yielding a scalable and semantically rich architecture for image generation. The full generation pipeline can be interpreted in two training stages:
- Stage 1: Discrete Tokenization via VQ-GAN. An image is encoded into a grid of latent vectors by a convolutional encoder. Each vector is quantized to its nearest neighbor in a learned codebook. A CNN decoder reconstructs the image from these discrete tokens. The training objective incorporates adversarial realism, perceptual similarity, and vector quantization consistency.
- Stage 2: Autoregressive Modeling. A transformer is trained on token indices to model their spatial dependencies. It learns to predict each token based on preceding ones, enabling both unconditional and conditional sampling during generation.
This decoupling of local perceptual encoding from global generative modeling enables VQ-GAN to achieve the best of both worlds: localized feature accuracy and long-range compositional control.
Enrichment 20.7.6.2: Training Objectives and Losses in VQ-GAN
The training of VQ-GAN centers around a perceptually informed autoencoding task. The encoder \( E \) maps an input image \( x \in \mathbb {R}^{H \times W \times 3} \) to a latent map \( \hat {z} = E(x) \in \mathbb {R}^{h \times w \times d} \), which is then quantized to \( z_q \in \mathcal {Z}^{h \times w} \) by nearest-neighbor lookup from a codebook of learned prototypes. The decoder \( G \) reconstructs the image \( \hat {x} = G(z_q) \). While this process resembles the original VQ-VAE [460], the loss function in VQ-GAN is significantly more expressive.
Total Loss The total objective used to train the encoder, decoder, and codebook jointly is: \[ \mathcal {L}_{\mbox{VQ-GAN}} = \lambda _{\mbox{rec}} \cdot \mathcal {L}_{\mbox{rec}} + \lambda _{\mbox{GAN}} \cdot \mathcal {L}_{\mbox{GAN}} + \mathcal {L}_{\mbox{VQ}} \] where each term is detailed below, and \( \lambda _{\mbox{rec}}, \lambda _{\mbox{GAN}} \) are hyperparameters (typically \( \lambda _{\mbox{rec}} = 1.0 \), \( \lambda _{\mbox{GAN}} = 1.0 \)).
1. Perceptual Reconstruction Loss \( \mathcal {L}_{\mbox{rec}} \) Rather than minimizing pixel-wise MSE, VQ-GAN uses a perceptual loss based on deep feature activations: \[ \mathcal {L}_{\mbox{rec}} = \frac {1}{C_l H_l W_l} \left \| \phi _l(x) - \phi _l(\hat {x}) \right \|_2^2 \] Here, \( \phi _l(\cdot ) \) denotes the activation map of a pre-trained VGG network at layer \( l \), and \( C_l, H_l, W_l \) are its dimensions. This encourages reconstructions that preserve semantic and texture-level similarity even if pixel-level details vary, helping avoid the blurriness seen in VQ-VAE outputs.
2. Adversarial Patch Loss \( \mathcal {L}_{\mbox{GAN}} \) To further enhance realism, VQ-GAN adds an adversarial loss using a multi-scale PatchGAN discriminator \( D \). This discriminator classifies local image patches as real or fake. The generator (i.e., encoder + quantizer + decoder) is trained with the hinge loss: \[ \mathcal {L}_{\mbox{GAN}}^{G} = -\mathbb {E}_{\hat {x}} [ D(\hat {x}) ] \quad , \quad \mathcal {L}_{\mbox{GAN}}^{D} = \mathbb {E}_{\hat {x}} [ \max (0, 1 + D(\hat {x})) ] + \mathbb {E}_{x} [ \max (0, 1 - D(x)) ] \] This formulation stabilizes adversarial training and ensures that reconstructions match the patch statistics of real images.
3. Vector Quantization Commitment and Codebook Loss \( \mathcal {L}_{\mbox{VQ}} \) The standard VQ loss is used to train the codebook and encourage encoder outputs to commit to discrete codes. Following [460], the loss is: \[ \mathcal {L}_{\mbox{VQ}} = \underbrace {\left \| \mbox{sg}[E(x)] - z_q \right \|_2^2}_{\mbox{Codebook loss}} + \beta \cdot \underbrace {\left \| E(x) - \mbox{sg}[z_q] \right \|_2^2}_{\mbox{Commitment loss}} \] where \( \mbox{sg}[\cdot ] \) is the stop-gradient operator, and \( \beta \) controls the strength of the commitment penalty (typically \( \beta = 0.25 \)).
Combined Optimization Strategy During training, the encoder, decoder, and codebook are updated to minimize \( \mathcal {L}_{\mbox{VQ-GAN}} \), while the discriminator is trained adversarially via \( \mathcal {L}_{\mbox{GAN}}^{D} \). Optimization alternates between these two steps using Adam with a 2:1 or 1:1 update ratio. The perceptual loss and discriminator feedback reinforce each other: one encourages semantically faithful reconstructions, the other pushes the generator to produce images indistinguishable from real data.
Why This Loss Works The combination of perceptual and adversarial losses compensates for the main weaknesses of prior methods. While VQ-VAE reconstructions are often blurry due to MSE, the perceptual loss helps match high-level content, and adversarial feedback ensures photo-realistic textures. This makes the quantized codebook entries more semantically meaningful, resulting in compressed representations that are useful for downstream transformer modeling.
Training Summary VQ-GAN training proceeds in two stages:
- 1.
- Stage 1: Autoencoding. The encoder, decoder, codebook, and discriminator are trained jointly using the perceptual, adversarial, and quantization losses. The model learns to represent images as discrete token grids with high perceptual quality.
- 2.
- Stage 2: Transformer Language Modeling. The autoencoder is frozen, and a transformer is trained on the flattened token sequences \( z_q \) using standard cross-entropy loss for next-token prediction.
This dual-stage training ensures that VQ-GAN not only compresses visual information effectively, but also produces discrete codes that are highly suitable for transformer-based generation.
Enrichment 20.7.6.3: Discrete Codebooks and Token Quantization
A central innovation in VQ-GAN lies in its use of a discrete latent space, where each spatial location in the encoder output is assigned an index corresponding to a learned codebook entry. This mechanism—first introduced in VQ-VAE [460]—forms the foundation for compressing images into compact, semantically meaningful tokens suitable for transformer-based modeling.
Latent Grid and Codebook Structure Let \( x \in \mathbb {R}^{H \times W \times 3} \) denote an image. The encoder \( E \) transforms it into a continuous latent map \( \hat {z} = E(x) \in \mathbb {R}^{h \times w \times d} \), where each spatial position \( (i, j) \) corresponds to a \( d \)-dimensional vector. The spatial resolution \( h \times w \) is typically much smaller than \( H \times W \), e.g., \( 16 \times 16 \) for \( 256 \times 256 \) images.
This latent map is then quantized into a discrete tensor \( z_q \in \mathcal {Z}^{h \times w} \) using a codebook \( \mathcal {Z} = \{ e_k \in \mathbb {R}^d \mid k = 1, \ldots , K \} \) containing \( K \) learnable embeddings (e.g., \( K = 1024 \)).
Nearest-Neighbor Quantization For each location \( (i,j) \), the vector \( \hat {z}_{i,j} \in \mathbb {R}^d \) is replaced by its closest codebook entry: \[ z_q(i,j) = e_k \quad \mbox{where} \quad k = \arg \min _{k'} \left \| \hat {z}_{i,j} - e_{k'} \right \|_2^2 \] This lookup converts the continuous feature map into a grid of discrete embeddings, each pointing to one of the \( K \) learned codebook vectors.
Gradient Flow via Stop-Gradient and Codebook Updates Because the argmin operation is non-differentiable, VQ-GAN uses the same trick as VQ-VAE: it copies the selected embedding \( e_k \) into the forward pass and blocks gradients from flowing into the encoder during backpropagation. Formally, the quantized output is written as: \[ z_q = \mbox{sg}(e_k) + (\hat {z} - \mbox{sg}(\hat {z})) \] where \( \mbox{sg}(\cdot ) \) denotes the stop-gradient operator.
To update the codebook entries \( \{ e_k \} \), the gradient is backpropagated from the reconstruction loss to the selected embeddings. This allows the codebook to adapt over time based on usage and reconstruction feedback.
Codebook Capacity and Token Usage The number of entries \( K \) in the codebook is a key hyperparameter. A small \( K \) leads to coarse quantization (less expressiveness), while a large \( K \) may overfit or lead to infrequent usage of some codes. VQ-GAN monitors token usage statistics during training to ensure that all codes are being used (via an exponential moving average of codebook assignments). This avoids codebook collapse.
Spatial Token Grid as Transformer Input After quantization, the grid \( z_q \in \mathbb {R}^{h \times w \times d} \) is flattened into a sequence of token indices \( \{k_1, \ldots , k_{hw}\} \in \{1, \ldots , K\}^{hw} \), forming the input for the transformer. The transformer learns to model the autoregressive distribution over this sequence: \[ p(k_1, \ldots , k_{hw}) = \prod _{t=1}^{hw} p(k_t \mid k_1, \ldots , k_{t-1}) \] These discrete tokens serve as the vocabulary of the transformer, analogous to word tokens in natural language processing.
Comparison to VQ-VAE-2 Unlike VQ-VAE-2, which uses multiple hierarchical codebooks to represent coarse-to-fine visual features, VQ-GAN uses a single spatially aligned codebook and compensates for the lack of hierarchy by injecting a stronger perceptual and adversarial training signal. This results in tokens that are rich in local structure and semantically coherent, making them more suitable for transformer-based modeling.
Summary The quantization mechanism in VQ-GAN compresses an image into a spatial grid of discrete tokens drawn from a learned embedding table. This enables efficient transformer training by decoupling high-resolution pixel processing from global token modeling. The next section explains how the transformer is trained on these token sequences to generate new images.
Enrichment 20.7.6.4: Autoregressive Transformer for Token Modeling
Once the VQ-GAN encoder and decoder are trained and the discrete codebook is stabilized, the model proceeds to its second stage: learning a generative model over token sequences. Rather than modeling images at the pixel level, this stage focuses on learning the probability distribution of the codebook indices that describe compressed image representations.
Token Sequence Construction After quantization, the encoder yields a spatial grid of token indices \( z_q \in \{1, \ldots , K\}^{h \times w} \). To apply sequence modeling, this 2D array is flattened into a 1D sequence \( \mathbf {k} = [k_1, \ldots , k_{N}] \), where \( N = h \cdot w \). Typically, this flattening is performed in row-major order, preserving local spatial adjacency as much as possible.
Autoregressive Training Objective A transformer decoder is trained to predict the next token given all previous ones. The learning objective is to maximize the log-likelihood of the true sequence: \[ \mathcal {L}_{\mbox{AR}} = - \sum _{t=1}^{N} \log p(k_t \mid k_1, \ldots , k_{t-1}) \] This objective is optimized using teacher forcing and standard cross-entropy loss. During training, the model is exposed to full sequences (obtained from the pretrained encoder) and learns to predict the next index at each position.
Positional Encoding and Embedding Table To preserve spatial context in the flattened sequence, each token is augmented with a positional encoding. This encoding \( \mbox{PE}(t) \in \mathbb {R}^d \) is added to the learned embedding \( e_{k_t} \), yielding the input to the transformer: \[ x_t = e_{k_t} + \mbox{PE}(t) \] The transformer layers then process this sequence via multi-head self-attention and feed-forward blocks.
Sampling for Image Generation At inference time, the transformer generates a new image by sampling from the learned token distribution:
- 1.
- Initialize with a special start token or random first token.
- 2.
- For \( t = 1 \) to \( N \), sample: \[ k_t \sim p(k_t \mid k_1, \ldots , k_{t-1}) \]
- 3.
- After all tokens are generated, reshape the sequence into a grid \( z_q \in \mathbb {R}^{h \times w} \), look up their embeddings from the codebook, and decode using the frozen VQ-GAN decoder.
Windowed Attention for Long Sequences Modeling large images requires long token sequences (e.g., \( 32 \times 32 = 1024 \) tokens for \( 256 \times 256 \) images). This creates a memory bottleneck for standard transformers due to the quadratic cost of self-attention. To address this, VQ-GAN adopts a sliding window or local attention mechanism: the transformer only attends to a fixed-size neighborhood of preceding tokens when predicting the next one. This approximation reduces computational complexity while preserving local coherence.
Comparison with Pixel-Level Modeling Unlike models that operate directly on pixels (e.g., PixelCNN or autoregressive GANs), this token-based approach offers:
- Lower sequence length: Tokens are downsampled representations, so fewer steps are needed.
- Higher abstraction: Each token represents a meaningful visual chunk (e.g., a part of an object), not just an individual pixel.
- Improved generalization: The transformer learns compositional rules over high-level image structure, rather than low-level noise.
Transformer Variants: Decoder-Only and Encoder–Decoder
The VQ-GAN framework employs different types of transformer architectures depending on the downstream task—ranging from autoregressive image generation to conditional image synthesis from natural language. The two primary transformer types are:
-
Decoder-only (GPT-style) Transformers: For unconditional and class-conditional image generation, VQ-GAN uses a causal decoder transformer inspired by GPT-2 [496]. This architecture models the token sequence left-to-right, predicting each token conditioned on the preceding tokens \(1, \cdots k\). It consists of stacked self-attention blocks with masked attention to preserve causality. The output is a probability distribution over codebook indices for the next token, enabling sequence generation via sampling. This design supports:
- Unconditional generation from a start-of-sequence token
- Class-conditional generation by appending a class token or embedding
-
Encoder–Decoder Transformers (Text-to-Image): For conditional generation from textual descriptions, the authors adopt a full Transformer encoder–decoder architecture—popularized by models like T5 [501] and BART [324]. Here, the encoder processes a sequence of text tokens (from a caption), typically encoded via pretrained embeddings (e.g., CLIP or BERT). The decoder then autoregressively generates image token sequences conditioned on the encoder output. This setup allows for:
- Cross-modal alignment between text and image
- Rich semantic guidance at every generation step
- Enhanced sample quality and relevance in text-to-image tasks
In both cases, the transformer operates over a compressed latent space of visual tokens, not pixels. This architectural choice drastically reduces sequence length (e.g., 16 × 16 = 256 16×16=256 tokens for 256 × 256 256×256 images), enabling efficient training while preserving global structure.
The authors also explore sliding-window attention during inference to reduce quadratic attention costs for long token sequences. This allows the model to scale beyond 256×256 resolution while maintaining tractability.
Training Setup All transformer variants are trained after the VQ-GAN encoder and decoder are frozen. The transformer is optimized using standard cross-entropy loss over codebook indices and trained to minimize next-token prediction error. This decoupling of training stages avoids instability and allows plug-and-play use of any transformer model atop a trained VQ-GAN tokenizer.
Summary The transformer in VQ-GAN learns an autoregressive model over discrete image tokens produced by the encoder and codebook. Its outputs—sequences of token indices—are used to synthesize novel images by decoding through the frozen decoder. In the next subsection, we explore the sampling process in detail and the role of quantization grid size in the fidelity and flexibility of the model.
Enrichment 20.7.6.5: Token Sampling and Grid Resolution
Once a transformer has been trained to model the distribution over token sequences, we can generate new images by sampling from this model. This process involves autoregressively generating a sequence of discrete token indices, reshaping them into a spatial grid, and then decoding them through the frozen decoder network.
Autoregressive Sampling Pipeline At inference time, generation proceeds as follows:
- 1.
- Start from a special start token or a randomly selected token index.
- 2.
- For each timestep \( t \in \{1, \ldots , N\} \), sample the next token index from the model’s predicted distribution: \[ k_t \sim p(k_t \mid k_1, \ldots , k_{t-1}) \]
- 3.
- After all \( N = h \cdot w \) tokens have been generated, reshape the sequence back to a 2D spatial grid.
- 4.
- Look up each token’s codebook embedding and pass the resulting tensor through the decoder to obtain the final image.
This sampling process is computationally expensive, as each new token depends on all previously generated tokens. For longer sequences (e.g., \(32 \times 32 = 1024\) tokens), decoding can be slow, especially without optimized parallel inference.
Impact of Latent Grid Resolution The spatial resolution of the latent token grid \( z_q \in \mathbb {R}^{h \times w} \) is determined by the encoder’s downsampling factor. For instance, with a \(4\times \) downsampling per spatial dimension, a \(256 \times 256\) image is compressed into a \(64 \times 64\) token grid. Larger \( h \times w \) grids provide finer granularity but also lead to longer token sequences for the transformer to model.
There is a trade-off here:
- Higher spatial resolution allows for more detailed reconstructions, especially at high image resolutions.
- Lower spatial resolution results in faster training and sampling but may lead to coarser images.
The authors of VQ-GAN found that using a \(16 \times 16\) token grid worked well for \(256 \times 256\) images, balancing model efficiency and output quality. However, when working with higher-resolution images, grid size becomes a bottleneck: the more aggressively the encoder downsamples, the more difficult it becomes to preserve fine spatial detail. On the other hand, increasing token count burdens the transformer with longer sequences and higher memory demands.
Sliding Window Attention (Optional Variant) To scale to longer sequences without quadratic memory costs, VQ-GAN optionally uses a sliding window attention mechanism. Rather than attending to all previous tokens, each position attends only to a fixed-size window of previous tokens (e.g., the last 256). This approximation significantly reduces memory requirements while preserving local consistency during generation.
Summary Sampling in VQ-GAN is a two-stage process: a transformer generates a sequence of codebook indices that are then decoded into an image. The grid resolution of the quantized latent space plays a critical role in the visual fidelity of outputs and the computational feasibility of training. While smaller grids reduce complexity, larger grids improve detail—highlighting the importance of choosing an appropriate balance for the task at hand.
Enrichment 20.7.6.6: VQ-GAN: Summary and Outlook
VQ-GAN [148] represents a pivotal step in the evolution of generative models by bridging the efficiency of discrete latent modeling with the expressive power of transformers. Its design merges the local inductive strengths of convolutional encoders and decoders with global autoregressive modeling in latent space, enabling synthesis of high-resolution and semantically coherent images. The key ingredients of this system include:
- A convolutional autoencoder with vector quantization to compress high-dimensional images into discrete token grids.
- A codebook trained using perceptual and adversarial losses to produce reconstructions that are sharp and semantically rich.
- An autoregressive transformer that learns to model spatial dependencies among tokens in the latent space, enabling sample generation and manipulation.
Why VQ-GAN Works By introducing adversarial and perceptual supervision into the training of the autoencoder, VQ-GAN overcomes a major limitation of previous models like VQ-VAE and VQ-VAE-2: the tendency toward blurry or oversmoothed reconstructions. The perceptual loss aligns high-level features between generated and ground-truth images, while the patch-based adversarial loss encourages fine detail, particularly texture and edges. Meanwhile, transformers provide a mechanism for globally coherent synthesis by modeling long-range dependencies among latent tokens.
This decoupling of low-level reconstruction and high-level compositionality makes VQ-GAN not only effective but modular. The decoder and transformer can be trained separately, and the codebook can serve as a compact representation for a wide range of downstream tasks.
Future Directions and Influence The modular, tokenized view of image generation introduced by VQ-GAN has had wide-reaching consequences in the field of generative modeling:
- It laid the foundation for powerful text-to-image models like DALLE [509] and followup versions of it, which leverage learned discrete tokens over visual content as a bridge to language.
- The taming-transformers framework became a baseline for generative pretraining and fine-tuning, influencing both the latent diffusion models (LDMs) [531] and modern image editing applications like Stable Diffusion.
- Its discrete latent representation also enabled efficient semantic image manipulation, inpainting, and zero-shot transfer by training lightweight models directly in token space.
In conclusion, VQ-GAN exemplifies how a principled integration of discrete representation learning, adversarial training, and autoregressive modeling can lead to scalable, controllable, and high-fidelity generation. It forms a crucial bridge between convolutional perception and tokenized generative reasoning, and it remains a foundational method in modern generative visual pipelines.
Enrichment 20.8: Additional Important GAN Works
In addition to general-purpose GANs and high-resolution synthesis frameworks, many architectures have been proposed to address specific structured generation tasks—ranging from super-resolution and paired image translation to semantic layout synthesis and motion trajectory forecasting. These models extend adversarial learning to incorporate spatial, semantic, and temporal constraints, often introducing novel conditioning mechanisms, domain priors, and loss formulations.
We begin with seminal architectures such as SRGAN [317] for perceptual super-resolution, pix2pix [255] and CycleGAN [805] for paired and unpaired image translation, SPADE [470] for semantic-to-image generation via spatially-adaptive normalization, and SocialGAN [198] for trajectory prediction in dynamic social environments. These models exemplify how GANs can be tailored to specific applications by redesigning generator–discriminator objectives and conditioning pipelines.
If further exploring recent innovations is of interest, we also recommend reviewing cutting-edge hybrid architectures such as GauGAN2, which fuses semantic maps with text prompts for fine-grained control over scene layout and appearance, and Diffusion-GAN hybrids [313], which combine score-based denoising processes with adversarial training for enhanced realism and robustness. These models reflect emerging trends in generative modeling—blending expressive priors, multimodal conditioning, and stable learning strategies across increasingly complex synthesis domains.
We now proceed to analyze the foundational task-specific GANs in greater depth, each marking a significant step forward in aligning generative modeling with real-world objectives.
Enrichment 20.8.1: SRGAN: Photo-Realistic Super-Resolution
SRGAN [317] introduced the first GAN-based framework for perceptual single-image super-resolution, achieving photo-realistic results at \(4\times \) upscaling. Rather than optimizing conventional pixel-level losses such as Mean Squared Error (MSE), which are known to favor high PSNR but overly smooth outputs, SRGAN proposes a perceptual training objective that aligns better with human visual preferences. This objective combines adversarial realism with deep feature similarity extracted from a pre-trained classification network (VGG16).
Motivation and Limitations of Pixel-Wise Supervision Pixel-based metrics such as MSE or L2 loss tend to produce blurry reconstructions, particularly at large upscaling factors (e.g., \(4\times \)), because they penalize even slight misalignments in fine details. If multiple plausible high-resolution reconstructions exist for a single low-resolution input, the network trained with MSE will learn to output the average of those possibilities—resulting in smooth textures and a loss of perceptual sharpness.
While pixel-wise accuracy is mathematically well-defined, it does not always reflect visual fidelity. To address this, SRGAN replaces the MSE loss with a perceptual loss that compares images in a feature space defined by deep activations of a pre-trained VGG16 network. These intermediate features reflect higher-level abstractions (edges, textures, object parts), which are more aligned with how humans perceive image realism.
Why Use VGG-Based Perceptual Loss? The VGG-based content loss compares the reconstructed image \( \hat {I}_{SR} \) and the ground truth image \( I_{HR} \) not at the pixel level, but in the feature space of a neural network trained for image classification.
Concretely, if \( \phi _{i,j}(\cdot ) \) represents the activations at the \( (i,j) \)-th layer of VGG16, then the perceptual loss is defined as: \[ \mathcal {L}_{\mbox{VGG}} = \frac {1}{W H} \sum _{x,y} \left \| \phi _{i,j}(I_{HR})_{x,y} - \phi _{i,j}(\hat {I}_{SR})_{x,y} \right \|_2^2 \] This loss better preserves fine-grained textures and edges, as it penalizes semantic-level mismatches. Although this approach sacrifices raw PSNR scores, it substantially improves perceptual quality.
Architecture Overview The SRGAN generator is a deep convolutional network consisting of:
- An initial \( 9 \times 9 \) convolution followed by Parametric ReLU (PReLU).
- 16 residual blocks, each comprising two \(3 \times 3\) convolutions with PReLU and skip connections.
- A global skip connection from the input to the output of the residual stack.
- Two sub-pixel convolution blocks (pixel shuffling [564]) to increase spatial resolution by a factor of 4 in total. Each block first applies a learned convolution that expands the number of channels by a factor of \( r^2 \), where \( r \) is the upscaling factor. Then, the resulting feature map is rearranged using a pixel shuffle operation that reorganizes the channels into spatial dimensions. This process allows efficient and learnable upsampling while avoiding checkerboard artifacts commonly associated with transposed convolutions. The rearrangement step transforms a tensor of shape \( H \times W \times (r^2 \cdot C) \) into \( (rH) \times (rW) \times C \), effectively increasing image resolution without introducing new spatial operations.
- A final \(9 \times 9\) convolution with Tanh activation to produce the RGB image.
Skip connections are critical to the generator’s stability and learning efficiency. They allow the network to propagate low-frequency structure (e.g., colors, global layout) directly from the input to the output, enabling the residual blocks to focus solely on learning high-frequency textures and refinements. This decomposition aligns well with the structure-versus-detail duality in image synthesis.
Upsampling Strategy: Sub-Pixel Convolution Blocks A core challenge in super-resolution is learning how to upscale low-resolution inputs into high-resolution outputs while preserving structural integrity and synthesizing high-frequency texture. Traditional interpolation methods such as nearest-neighbor, bilinear, or bicubic are non-parametric—they ignore image content and apply fixed heuristics, often producing smooth but unrealistic textures. Learnable alternatives like transposed convolutions introduce adaptive filters but are known to suffer from checkerboard artifacts due to uneven kernel overlap and gradient instability.
To address these limitations, SRGAN employs sub-pixel convolution blocks, first introduced in ESPCN [564]. Rather than directly increasing spatial resolution, the network instead increases the channel dimension of intermediate features. Specifically, given a desired upscaling factor \( r \), the model outputs a tensor of shape \( H \times W \times (C \cdot r^2) \). This tensor is then passed through a deterministic rearrangement operation called the pixel shuffle, which converts it to a higher-resolution tensor of shape \( rH \times rW \times C \). This process can be visualized as splitting the interleaved channels into spatial neighborhoods—each group of \( r^2 \) channels at a given location forms a distinct \( r \times r \) patch in the upsampled output.
Formally, for a given low-resolution feature map \( F \in \mathbb {R}^{H \times W \times (C \cdot r^2)} \), the pixel shuffle operation rearranges it into \( \tilde {F} \in \mathbb {R}^{rH \times rW \times C} \) via: \[ \tilde {F}(r \cdot i + a, r \cdot j + b, c) = F(i, j, c \cdot r^2 + a \cdot r + b) \] for \( i \in [0, H-1], j \in [0, W-1], a, b \in [0, r-1], c \in [0, C-1] \). This operation is non-parametric and fully differentiable.
This upsampling strategy provides several key benefits:
- It keeps most computation in the low-resolution domain, improving speed and memory efficiency.
- Unlike transposed convolutions, it avoids overlapping kernels, which reduces aliasing and checkerboard artifacts.
- Because the convolution preceding the pixel shuffle is learned, the network can generate content-aware and semantically rich upsampling filters.
However, sub-pixel convolution is not without drawbacks. The hard-coded spatial rearrangement makes it less flexible for modeling long-range spatial dependencies, which must be learned indirectly by preceding convolutional layers.
This mechanism is now widely adopted in modern super-resolution networks, where it strikes an effective balance between learnability, visual quality, and computational efficiency.
Discriminator Design The discriminator is a VGG-style fully convolutional network that:
- Applies a sequence of \(3 \times 3\) convolutions with increasing numbers of filters.
- Reduces spatial resolution using strided convolutions (no max pooling).
- Uses LeakyReLU activations and BatchNorm.
- Ends with two dense layers and a final sigmoid activation to classify images as real or fake.
Together, the generator and discriminator are trained in an adversarial framework, where the discriminator learns to distinguish between real and super-resolved images, and the generator learns to fool the discriminator while also minimizing perceptual content loss.
In summary, SRGAN’s perceptual training framework—rooted in feature-level losses and adversarial feedback—transformed the super-resolution landscape. It shifted the focus from purely quantitative fidelity (e.g., PSNR) to perceptual realism, influencing numerous follow-up works in both restoration and generation.
Perceptual Loss Function Let \( \phi _{i,j}(\cdot ) \) denote the feature maps extracted from the \((i,j)\)-th layer of the pretrained VGG19 network. The total perceptual loss used to train SRGAN is: \[ \mathcal {L}_{\mbox{SR}} = \underbrace {\frac {1}{WH} \sum _{x,y} \| \phi _{i,j}(I_{HR})_{x,y} - \phi _{i,j}(\hat {I}_{SR})_{x,y} \|_2^2}_{\mbox{Content Loss (VGG Feature Matching)}} + \lambda \cdot \underbrace {-\log D(\hat {I}_{SR})}_{\mbox{Adversarial Loss}} \] where \( \lambda = 10^{-3} \) balances the two terms.
- Phase 1: Pretrain the generator \( G \) as a ResNet (SRResNet) with MSE loss to produce strong initial reconstructions.
- Phase 2: Jointly train \( G \) and the discriminator \( D \) using the perceptual loss above.
- Generator uses ParametricReLU activations and sub-pixel convolutions [564] for efficient upscaling.
- Discriminator architecture follows DCGAN [495] conventions: LeakyReLU activations, strided convolutions, and no max pooling.
Quantitative and Perceptual Results Despite having lower PSNR than SRResNet, SRGAN consistently achieves higher Mean Opinion Scores (MOS) in human evaluations, indicating more photo-realistic outputs. Tested in experiments on datasets like Set5, Set14, and BSD100.
Enrichment 20.8.2: pix2pix: Paired Image-to-Image Translation with cGANs
Motivation and Formulation The pix2pix framework [255] addresses a family of image-to-image translation problems where we are given paired training data \( \{ (x_i, y_i) \} \), with the goal of learning a mapping \( G: x \mapsto y \) from input images \( x \) (e.g., segmentation masks, sketches, grayscale images) to output images \( y \) (e.g., photos, maps, colored images).
While fully convolutional neural networks (CNNs) can be trained to minimize an L2 or L1 loss between the generated output and the ground truth, such approaches tend to produce blurry results. This is because the pixel-wise losses average over all plausible outputs, failing to capture high-frequency structure or visual realism.
Instead of hand-designing task-specific loss functions, the authors propose using a conditional GAN (cGAN) objective. The discriminator \( D \) is trained to distinguish between real pairs \( (x, y) \) and fake pairs \( (x, G(x)) \), while the generator \( G \) learns to fool the discriminator. This adversarial training strategy encourages the generator to produce outputs that are not just pixel-wise accurate, but also indistinguishable from real images in terms of texture, edges, and fine details.
This general-purpose approach enables the same model and training procedure to be applied across a wide range of problems—without modifying the loss function or architecture—highlighting the power of adversarial learning to implicitly learn appropriate loss functions that enforce realism.
Enrichment 20.8.2.1: Generator Architecture and L1 Loss
Generator Architecture: U-Net with Skip Connections The pix2pix generator adopts a U-Net-style encoder–decoder architecture tailored for structured image-to-image translation. Its goal is to transform a structured input image \( x \) (such as an edge map, semantic label mask, or sketch) into a realistic output \( y \), preserving both spatial coherence and semantic fidelity.
A common failure mode of vanilla encoder-decoder CNNs is their tendency to blur or oversmooth outputs. This is because spatial resolution is reduced during encoding, and then the decoder must regenerate fine details from heavily compressed features—often losing important low-level cues such as edges and textures.
To overcome this, pix2pix integrates skip connections that link each encoder layer to its corresponding decoder layer. This structure is inspired by the U-Net architecture originally designed for biomedical segmentation tasks (see §15.6). The idea is to concatenate feature maps from early encoder layers (which contain high-frequency, low-level spatial information) directly into the decoder pathway, providing detailed cues that help the generator synthesize accurate textures, contours, and spatial alignment.
While the architecture is based on U-Net, pix2pix introduces several important differences:
- The generator is trained adversarially as part of a conditional GAN setup, rather than with a pixel-wise classification or regression loss.
- The input–output pairs often differ semantically (e.g., segmentation maps vs. RGB images), requiring stronger representational flexibility.
- Noise is not injected through a latent vector \( z \); instead, pix2pix introduces stochasticity via dropout layers applied at both training and inference time.
This design allows the generator to be both expressive and detail-preserving, making it well-suited for translation tasks where structural alignment between input and output is critical.
The Role of L1 Loss In addition to the adversarial objective, pix2pix uses a pixel-wise L1 loss between the generated image \( G(x) \) and the ground truth image \( y \). Formally, this term is: \[ \mathcal {L}_{L1}(G) = \mathbb {E}_{x,y} \left [ \| y - G(x) \|_1 \right ] \] This loss encourages the generator to output images that are structurally aligned with the target and reduces the risk of mode collapse. The authors argue that L1 is preferable to L2 (mean squared error) because it encourages less blurring. While L2 loss disproportionately penalizes large errors and promotes averaging over plausible solutions (leading to overly smooth results), L1 penalizes errors linearly and retains sharper detail.
The addition of L1 loss provides a simple yet powerful inductive constraint: while the adversarial loss encourages outputs to “look real,” the L1 loss ensures they are aligned with the target. This combination was shown to reduce blurring substantially and is critical for tasks where pixel-level structure matters.
Why Not WGAN or WGAN-GP? While more theoretically grounded adversarial objectives—such as the Wasserstein GAN [14] or WGAN-GP [194]—had already been introduced by the time of pix2pix’s publication, the authors found these alternatives to underperform empirically in their setting.
Specifically, they observed that standard GAN training with a conditional discriminator resulted in sharper edges and more stable convergence across a range of datasets. Therefore, pix2pix adopts the original GAN loss [180], modified for the conditional setting (described in detail in a later section).
Enrichment 20.8.2.2: Discriminator Design and PatchGAN
Discriminator Design and Patch-Level Realism (PatchGAN) In pix2pix, the discriminator is designed to operate at the level of local patches rather than entire images. This design—known as the PatchGAN discriminator—focuses on classifying whether each local region of the output image \( y \) is realistic and consistent with the corresponding region in the input \( x \). Instead of outputting a single scalar value, the discriminator produces a grid of probabilities, one per patch, effectively modeling image realism as a Markov random field.
Architecture: The PatchGAN discriminator is a fully convolutional network that receives as input the concatenation of the input image \( x \) and the output image \( y \) (either real or generated), stacked along the channel dimension. This stacked tensor \( [x, y] \in \mathbb {R}^{H \times W \times (C_x + C_y)} \) is then processed by a series of convolutional layers with stride \(2\), producing a downsampled feature map of shape \( N \times N \), where each value lies in \( [0, 1] \). Each scalar in this output grid corresponds to a specific receptive field (e.g., \(70 \times 70\) pixels in the input image) and reflects the discriminator’s estimate of the realness of that patch—i.e., whether that patch of \( y \), given \( x \), looks realistic and properly aligned.
What the Discriminator Learns: Importantly, the patches that are judged “real” or “fake” come from the output image \( y \), not the input \( x \). The conditioning on \( x \) allows the discriminator to assess whether each region of \( y \) is not only photorealistic but also semantically consistent with the structure of \( x \). This conditioning mechanism is crucial in tasks such as label-to-image translation, where the spatial alignment of objects is important.
Benefits: The PatchGAN discriminator has several advantages:
- It generalizes across image sizes since it is fully convolutional.
- It promotes high-frequency correctness, which encourages the generator to focus on local realism such as textures and edges.
Thus, rather than making a holistic judgment over the entire image, the discriminator acts as a texture and detail critic, applied densely across the image surface.
Objective: The discriminator in pix2pix is trained using the original GAN objective [180], adapted to the conditional setting. The discriminator \( D \) receives both the input image \( x \) and the output image—either the real \( y \sim p_{\mbox{data}}(y \mid x) \) or the generated output \( G(x) \). The discriminator is fully convolutional and produces a spatial grid of predictions rather than a single scalar, making it a PatchGAN.
Each element in the discriminator’s output grid corresponds to a local patch (e.g., \(70 \times 70\) pixels) in the image, and represents the discriminator’s estimate of whether that patch is “real” or “fake,” conditioned on \( x \). The overall discriminator loss is averaged across this grid: \[ \mathcal {L}_{D} = \mathbb {E}_{x,y} \left [ \log D(x, y) \right ] + \mathbb {E}_{x} \left [ \log (1 - D(x, G(x))) \right ] \]
Likewise, the adversarial component of the generator’s objective is: \[ \mathcal {L}_{G}^{\mbox{adv}} = \mathbb {E}_{x} \left [ \log (1 - D(x, G(x))) \right ] \]
Since the outputs of \( D \) are now grids of probabilities (one per receptive field region), the log terms are applied elementwise and the expectation denotes averaging across the training batch and spatial positions. In implementation, this is usually done using a mean over the entire \( N \times N \) output map.
Benefits of Patch-Based Discrimination:
- Reduced complexity: PatchGAN has fewer parameters and is easier to train than a global discriminator.
- High-frequency sensitivity: It is particularly good at enforcing local texture realism and preserving fine-grained detail.
- Fully convolutional: Since the model operates locally, it can be seamlessly applied to images of varying resolution at test time.
In the pix2pix paper, a \(70 \times 70\) receptive field is used, referred to as the \(70\)-PatchGAN, which balances context and texture fidelity. Smaller receptive fields may ignore global structure, while larger fields increase training difficulty and instability.
Having established the adversarial loss, we now examine the L1 reconstruction loss, which complements the discriminator by promoting spatial alignment and reducing blurriness in the generator output. Let me know when you’re ready to continue.
Enrichment 20.8.2.3: Full Training Objective and Optimization
Generator Loss: Combining Adversarial and Reconstruction Objectives While adversarial training encourages realism in the generated outputs, it does not ensure that the output matches the expected ground truth \( y \) in structured tasks such as semantic segmentation or image-to-image translation. For example, without additional supervision, the generator could produce an image that looks realistic but fails to reflect the precise layout or identity present in the input \( x \).
To address this, pix2pix adds an L1 loss between the generated output \( G(x) \) and the target image \( y \). The full generator loss becomes: \[ \mathcal {L}_{G} = \mathcal {L}_{G}^{\mbox{adv}} + \lambda \cdot \mathcal {L}_{\mbox{L1}} \] \[ \mbox{with} \quad \mathcal {L}_{\mbox{L1}} = \mathbb {E}_{x,y} \left [ \| y - G(x) \|_1 \right ] \]
Here, \( \lambda \) is a hyperparameter (typically set to \( \lambda = 100 \)) that balances the trade-off between fidelity to the ground truth and perceptual realism. The L1 loss is preferred over L2 (MSE) because it produces less blurring—a crucial feature for preserving edges and structural alignment.
This combined objective offers the best of both worlds:
- The adversarial loss encourages outputs that reside on the manifold of natural images.
- The L1 loss ensures spatial and semantic coherence between the prediction and the actual output.
The final optimization problem for the generator is: \[ G^* = \arg \min _{G} \max _{D} \mathcal {L}_{\mbox{cGAN}}(G, D) + \lambda \cdot \mathcal {L}_{\mbox{L1}}(G) \] where \( \mathcal {L}_{\mbox{cGAN}} \) denotes the conditional GAN loss using the PatchGAN discriminator: \[ \mathcal {L}_{\mbox{cGAN}}(G, D) = \mathbb {E}_{x,y} \left [ \log D(x, y) \right ] + \mathbb {E}_{x} \left [ \log (1 - D(x, G(x))) \right ] \]
Together, this objective promotes outputs that are not only indistinguishable from real images but also tightly aligned with the conditional input. The addition of L1 loss proved essential for stabilizing training, especially early in optimization when adversarial feedback is still weak or noisy.
We now conclude this overview of pix2pix with a summary of the use cases and real-world applications from the original paper.
Enrichment 20.8.2.4: Summary and Generalization Across Tasks
The core insight of pix2pix [255] is that many structured prediction tasks in computer vision—such as semantic segmentation, edge-to-photo conversion, and sketch-to-image generation—can be unified under the framework of conditional image translation. Rather than hand-designing task-specific loss functions, the GAN-based strategy learns a loss function implicitly through the discriminator, trained to judge how well an output image matches the target distribution given the input.
This conditional GAN setup—combined with a strong L1 reconstruction prior and a PatchGAN discriminator—proved surprisingly effective across a wide variety of domains. Figure 20.50 showcases representative examples from the original paper across multiple datasets and tasks.
Importantly, the pix2pix framework assumes access to paired training data—i.e., aligned input–output image pairs \( (x, y) \). In practice, however, such datasets are often expensive or infeasible to collect. For instance, we might have access to photos of horses and zebras, but no one-to-one mapping between them.
This limitation motivated a follow-up line of research into unpaired image-to-image translation, where models learn to transfer style, texture, or semantics between two domains without explicitly aligned data. The seminal work in this space is CycleGAN [805], which we explore next. It introduces a cycle-consistency loss that allows training without paired examples, opening the door to powerful translation tasks such as horse-to-zebra, summer-to-winter, and Monet-to-photo.
Enrichment 20.8.3: CycleGAN: Unpaired Image-to-Image Translation
Enrichment 20.8.3.1: Motivation: Beyond Paired Supervision in Image Translation
While pix2pix (see Enrichment 20.8.1) demonstrated the power of conditional GANs for paired image-to-image translation, its applicability is fundamentally limited by the need for aligned training pairs \((x, y)\)—that is, input images and their exact corresponding target images. In many practical domains, such as translating between artistic styles, seasons, or weather conditions, paired data is either unavailable or prohibitively expensive to collect.
CycleGAN [805] tackles this challenge by proposing an unsupervised framework that learns mappings between two visual domains \(X\) and \(Y\) using only unpaired collections of images from each domain. The central question becomes: How can we learn a function \(G: X \to Y\) when no direct correspondences exist?
Key Insight: Cycle Consistency
At the heart of CycleGAN is the cycle consistency constraint, a principle that enables learning from unpaired datasets. The system consists of two generators: \( G: X \rightarrow Y \), which maps images from domain \( X \) to domain \( Y \), and \( F: Y \rightarrow X \), which learns the reverse mapping.
The intuition is that if we start with an image \( x \) from domain \( X \), translate it to \( Y \) via \( G \), and then map it back to \( X \) via \( F \), the reconstructed image \( F(G(x)) \) should closely resemble the original \( x \). Likewise, for any \( y \in Y \), \( G(F(y)) \approx y \). This cycle consistency enforces that neither mapping is allowed to lose or invent too much information: the transformations should be approximately invertible and content-preserving.
Why does this help with unpaired data? Without paired supervision, there are infinitely many functions that can map the distribution of \( X \) to \( Y \) in a way that fools a GAN discriminator. However, most such mappings would destroy the underlying content, yielding images that are realistic in appearance but semantically meaningless. By explicitly requiring \( F(G(x)) \approx x \) and \( G(F(y)) \approx y \), CycleGAN dramatically restricts the space of possible solutions.
The network learns to transfer style while keeping the essential structure or identity intact, making unsupervised image-to-image translation feasible.
Enrichment 20.8.3.2: Typical Use Cases
CycleGAN’s framework has been widely adopted in domains where paired data is scarce or unavailable, including:
- Artistic style transfer (e.g., photographs \(\leftrightarrow \) Monet or Van Gogh paintings)
- Season or weather translation (e.g., summer \(\leftrightarrow \) winter, day \(\leftrightarrow \) night)
- Object transfiguration (e.g., horse \(\leftrightarrow \) zebra, apple \(\leftrightarrow \) orange)
Caution: Although CycleGAN and similar generative methods have attracted attention in medical imaging (e.g., MRI \(\leftrightarrow \) CT translation), their use in this context is highly controversial and potentially dangerous. There is growing evidence in the literature and community commentaries that generative models can hallucinate critical features—such as tumors or lesions—that do not exist in the real patient scan, or fail to preserve vital diagnostic information. Thus, care must be taken to avoid uncritical or clinical use of unpaired translation networks in safety-critical domains; for further discussion, see [110, 736].
This motivation sets the stage for the architectural design and learning objectives of CycleGAN, which we discuss next.
Enrichment 20.8.3.3: CycleGAN Architecture: Dual Generators and Discriminators
CycleGAN consists of two generators and two discriminators:
- Generator \( G: X \rightarrow Y \): Translates an image from domain \( X \) (e.g., horse) to domain \( Y \) (e.g., zebra).
- Generator \( F: Y \rightarrow X \): Translates an image from domain \( Y \) back to domain \( X \).
- Discriminator \( D_Y \): Distinguishes between real images \( y \) in domain \( Y \) and generated images \( G(x) \).
- Discriminator \( D_X \): Distinguishes between real images \( x \) in domain \( X \) and generated images \( F(y) \).
Each generator typically uses an encoder–decoder architecture with residual blocks, while the discriminators are PatchGANs (see enrichment 20.8.2.2.0), focusing on local realism rather than global classification.
The dual generator–discriminator setup allows CycleGAN to simultaneously learn both forward and reverse mappings, supporting unsupervised translation in both directions.
Enrichment 20.8.3.4: CycleGAN: Loss Functions and Training Objectives
Adversarial Loss: Least Squares GAN (LSGAN)
A central goal in CycleGAN is to ensure that each generator produces images that are indistinguishable from real images in the target domain. Rather than relying on the standard GAN log-likelihood loss, CycleGAN adopts the Least Squares GAN (LSGAN) objective [416], which stabilizes training and yields higher-fidelity results.
For generator \(G: X \rightarrow Y\) and discriminator \(D_Y\), the LSGAN adversarial loss is: \[ \mathcal {L}_{\mbox{GAN}}^{\mbox{LS}}(G, D_Y, X, Y) = \mathbb {E}_{y \sim p_{\mbox{data}}(y)} \left [ (D_Y(y) - 1)^2 \right ] + \mathbb {E}_{x \sim p_{\mbox{data}}(x)} \left [ (D_Y(G(x)))^2 \right ] \] This encourages the discriminator to output 1 for real images and 0 for fake (generated) images. Simultaneously, the generator is trained to fool the discriminator by minimizing: \[ \mathcal {L}_G^{\mbox{LS}} = \mathbb {E}_{x \sim p_{\mbox{data}}(x)} \left [ (D_Y(G(x)) - 1)^2 \right ] \] An identical adversarial loss is used for the reverse mapping (\(F: Y \rightarrow X\), \(D_X\)). The least squares loss is empirically more stable and less prone to vanishing gradients than the original log-loss formulation.
Cycle Consistency Loss
The cycle consistency loss is what enables learning with unpaired data. If we translate an image from domain \(X\) to \(Y\) via \(G\), and then back to \(X\) via \(F\), we should recover the original image: \(F(G(x)) \approx x\). The same logic holds for the reverse direction, \(G(F(y)) \approx y\). This is enforced via an L1 loss: \[ \mathcal {L}_{\mbox{cyc}}(G, F) = \mathbb {E}_{x \sim p_{\mbox{data}}(x)} \left [ \| F(G(x)) - x \|_1 \right ] + \mathbb {E}_{y \sim p_{\mbox{data}}(y)} \left [ \| G(F(y)) - y \|_1 \right ] \] The use of L1 loss (mean absolute error) in CycleGAN is deliberate and particularly suited for image reconstruction tasks. While L2 loss (mean squared error) is commonly used in regression settings, it has the tendency to penalize large errors more harshly and to average out possible solutions. In the context of image translation, this averaging effect often leads to over-smoothed and blurry outputs, especially when multiple plausible reconstructions exist.
In contrast, L1 loss treats all deviations linearly and is less sensitive to outliers, which makes it better at preserving sharp edges, fine details, and local structure in the generated images. Empirically, optimizing with L1 encourages the network to maintain crisp boundaries and avoids the tendency of L2 to ”wash out” high-frequency content. As a result, L1 loss is a better fit for the cycle consistency objective, promoting reconstructions that are visually sharper and closer to the original input.
Identity Loss (Optional)
To further regularize the mappings—especially when color or global content should remain unchanged (e.g., in style transfer)—CycleGAN optionally employs an identity loss: \[ \mathcal {L}_{\mbox{identity}}(G, F) = \mathbb {E}_{y \sim p_{\mbox{data}}(y)} \left [ \| G(y) - y \|_1 \right ] + \mathbb {E}_{x \sim p_{\mbox{data}}(x)} \left [ \| F(x) - x \|_1 \right ] \] This penalizes unnecessary changes to images already in the target domain.
Summary
The adversarial losses ensure that generated images in both directions are indistinguishable from real samples, while the cycle consistency and (optionally) identity losses force the learned mappings to preserve core content and structure. The overall objective is a weighted sum of these components: \[ \mathcal {L}_{\mbox{total}}(G, F, D_X, D_Y) = \mathcal {L}_{\mbox{GAN}}^{\mbox{LS}}(G, D_Y, X, Y) + \mathcal {L}_{\mbox{GAN}}^{\mbox{LS}}(F, D_X, Y, X) + \lambda _{\mbox{cyc}} \mathcal {L}_{\mbox{cyc}}(G, F) + \lambda _{\mbox{id}} \mathcal {L}_{\mbox{identity}}(G, F) \] where \(\lambda _{\mbox{cyc}}\) and \(\lambda _{\mbox{id}}\) are hyperparameters.
Enrichment 20.8.3.5: Network Architecture and Practical Training Considerations
Generator and Discriminator Architectures
Generators: CycleGAN employs a ResNet-based generator for both \(G: X \rightarrow Y\) and \(F: Y \rightarrow X\). Each generator typically consists of an initial convolutional block, followed by several residual blocks (commonly 6 or 9, depending on image size), and a set of upsampling (deconvolution) layers. Instance normalization and ReLU activations are used throughout to stabilize training and promote style flexibility. The design is chosen to enable both global and local transformations while maintaining content structure.
Discriminators: Both \(D_X\) and \(D_Y\) use a PatchGAN architecture—identical in spirit to the discriminator design in pix2pix (see Section Enrichment 20.8.1). Instead of classifying the entire image as real or fake, PatchGAN outputs a grid of real/fake probabilities, each associated with a spatial patch (e.g., \(70 \times 70\) pixels) in the input. This local focus encourages preservation of texture and style across the translated images, without requiring global image-level pairing.
Normalization and Activation: CycleGAN replaces batch normalization with instance normalization (see §7.14), which is especially beneficial for style transfer and image translation tasks. Unlike batch normalization, which normalizes feature statistics across the batch dimension, instance normalization computes the mean and variance independently for each sample and each channel, but only across the spatial dimensions \((H \times W)\). Specifically, for a given sample \(n\) and channel \(c\), instance normalization calculates: \[ \mu _{n,c} = \frac {1}{HW} \sum _{h=1}^{H} \sum _{w=1}^{W} x_{n,c,h,w}, \qquad \sigma ^2_{n,c} = \frac {1}{HW} \sum _{h=1}^{H} \sum _{w=1}^{W} \left (x_{n,c,h,w} - \mu _{n,c}\right )^2 \] and normalizes accordingly. This operation decouples the feature scaling from the batch and instead focuses normalization on the statistics of each individual sample and channel. As a result, instance normalization improves the consistency of style adaptation and translation, making it particularly well-suited for CycleGAN and similar works.
Training Strategy and Hyperparameters
The training procedure alternates between updating the generators (\(G\), \(F\)) and the discriminators (\(D_X\), \(D_Y\)). The total objective is a weighted sum of adversarial loss, cycle-consistency loss, and (optionally) identity loss: \[ \mathcal {L}_{\mbox{CycleGAN}} = \mathcal {L}_{\mbox{GAN}}(G, D_Y, X, Y) + \mathcal {L}_{\mbox{GAN}}(F, D_X, Y, X) + \lambda _{\mbox{cyc}}\mathcal {L}_{\mbox{cyc}}(G, F) + \lambda _{\mbox{id}}\mathcal {L}_{\mbox{identity}}(G, F) \] where \(\lambda _{\mbox{cyc}}\) and \(\lambda _{\mbox{id}}\) are hyperparameters controlling the importance of cycle and identity losses. Empirically, \(\lambda _{\mbox{cyc}} = 10\) is standard, and \(\lambda _{\mbox{id}}\) is set to \(0\) or \(0.5\) depending on the task.
Optimizers: CycleGAN uses the Adam optimizer, with \(\beta _1 = 0.5\) and \(\beta _2 = 0.999\), which are well-suited for stabilizing adversarial training.
Unpaired Data Setup: During each epoch, the model draws random samples from unpaired sets \(X\) and \(Y\), so every batch contains independently sampled images from both domains. This setup, along with cycle-consistency, enables effective learning without paired supervision.
Stabilizing Discriminator Training with a Fake Image Buffer To further stabilize adversarial training, CycleGAN maintains a buffer of previously generated fake images (typically 50) for each domain. When updating the discriminator, a random sample from this buffer is mixed with the most recent generated images. This approach prevents the discriminator from overfitting to the generator’s most current outputs, introduces greater diversity in the fake set, and improves convergence.
Enrichment 20.8.3.6: Ablation Study: Impact of Loss Components in CycleGAN
A comprehensive ablation study in CycleGAN systematically investigates the roles of the GAN loss, cycle-consistency loss, and their combinations. The results, as reported in the original CycleGAN paper [805], demonstrate that both adversarial (GAN) and cycle-consistency losses are critical for successful unpaired image-to-image translation.
Effect of Removing Loss Components
- Removing the GAN loss (using only cycle-consistency) produces outputs with preserved content but poor realism; the results lack natural appearance and often fail to match the target domain visually.
- Removing the cycle-consistency loss (using only adversarial loss) leads to mode collapse and lack of content preservation. The model may generate realistic-looking images, but they are often unrelated to the input and fail to capture the source structure.
- Cycle loss in only one direction (e.g., forward \(F(G(x)) \approx x\) or backward \(G(F(y)) \approx y\)) is insufficient and frequently causes training instability and mode collapse. The ablation reveals that bidirectional cycle consistency is essential for learning meaningful mappings without paired data.
Quantitative Results (from the CycleGAN Paper) The ablation is quantified using semantic segmentation metrics (per-pixel accuracy, per-class accuracy, and class IoU) evaluated on the Cityscapes dataset for both labels \(\rightarrow \) photo and photo \(\rightarrow \) labels directions. Tables 20.4 and 20.5 are directly reproduced from [805].
| Loss | Per-pixel acc. | Per-class acc. | Class IOU |
|---|---|---|---|
| Cycle alone | 0.22 | 0.07 | 0.02 |
| GAN alone | 0.51 | 0.11 | 0.08 |
| GAN + forward cycle | 0.55 | 0.18 | 0.12 |
| GAN + backward cycle | 0.39 | 0.14 | 0.06 |
| CycleGAN | 0.52 | 0.17 | 0.11 |
| Loss | Per-pixel acc. | Per-class acc. | Class IOU |
|---|---|---|---|
| Cycle alone | 0.10 | 0.05 | 0.02 |
| GAN alone | 0.53 | 0.11 | 0.07 |
| GAN + forward cycle | 0.49 | 0.11 | 0.07 |
| GAN + backward cycle | 0.01 | 0.06 | 0.01 |
| CycleGAN | 0.58 | 0.22 | 0.16 |
Qualitative Analysis The following figure visually compares the effects of different loss combinations. Removing either the GAN or cycle-consistency component leads to images that either lack realism (cycle alone) or ignore input structure (GAN alone, or single-direction cycle loss). The full CycleGAN model (with both losses in both directions) produces outputs that are both photorealistic and semantically aligned with the input.
Summary The ablation study conclusively shows that both adversarial and cycle-consistency losses are indispensable for successful unpaired image-to-image translation. The combination ensures the generated outputs are realistic, diverse, and semantically faithful to their source images, while avoiding mode collapse and degenerate mappings.
Enrichment 20.8.3.7: Summary and Transition to Additional Generative Approaches
The innovations introduced by CycleGAN have inspired a diverse ecosystem of task-specific GAN models, each adapting adversarial training to new modalities and challenges. Notable such works we won’t cover in-depth include:
- SPADE [470]: Semantic image synthesis using spatially-adaptive normalization, which achieves high-resolution generation from segmentation maps.
- SocialGAN [198]: Multimodal trajectory forecasting for socially-aware path prediction in crowds.
- MoCoGAN/VideoGAN [107]: Adversarial video generation architectures for modeling temporal dynamics in complex scenes.
Together, these models demonstrate the flexibility of adversarial learning in structured generation tasks. In the following sections, we broaden our view beyond GANs to introduce new families of generative approaches—including diffusion models and flow matching—that are rapidly advancing the state of the art in image, video, and sequential data synthesis.
Enrichment 20.9: Diffusion Models: Modern Generative Modeling
Enrichment 20.9.0.1: Motivation: Limitations of Previous Generative Models
Diffusion models have emerged as a powerful and principled approach to generative modeling, effectively addressing several longstanding challenges found in earlier generative paradigms. To appreciate their significance, it helps to briefly revisit these earlier approaches and clearly identify their main limitations:
Autoregressive Models (PixelCNN, PixelRNN, ...) Autoregressive models factorize the joint probability distribution into sequential conditional predictions, enabling exact likelihood computation and precise modeling of pixel-level dependencies. However, their inherently sequential nature severely limits sampling speed, making high-resolution synthesis prohibitively slow. Moreover, their reliance on local receptive fields often restricts global coherence and makes long-range dependencies difficult to model efficiently.
Variational Autoencoders (VAEs) VAEs provide efficient inference through latent variable modeling and offer stable training and sampling. Nonetheless, the assumption of independent Gaussian likelihoods at the output leads to blurred images and limited sharpness. Additionally, VAEs are vulnerable to posterior collapse, where the latent representation becomes underutilized, reducing expressivity and diversity in generated outputs.
Generative Adversarial Networks (GANs) GANs achieve impressive realism by optimizing an adversarial objective, bypassing explicit likelihood computation. Despite their success, GANs notoriously suffer from instability during training, sensitivity to hyperparameters, and mode collapse, where the generator focuses on a narrow subset of the data distribution. Furthermore, their lack of explicit likelihood estimation complicates evaluation and interpretability.
Hybrid Approaches (VQ-VAE, VQ-GAN) Hybrid models such as VQ-VAE and VQ-GAN combine discrete latent representations with autoregressive or adversarial priors. These methods partially address the shortcomings of VAEs and GANs but introduce their own issues, such as quantization artifacts, limited expressivity due to often codebook collapse, and computational inefficiency in latent space sampling.
The Case for Diffusion Models Diffusion models naturally overcome many of the above limitations by modeling data generation as the gradual reversal of a diffusion (noise-adding) process. Specifically, they offer:
- Stable and Robust Training: Diffusion models avoid adversarial training entirely, leading to stable and reproducible optimization.
- Explicit Likelihood Estimation: Their probabilistic framework supports tractable likelihood estimation, aiding interpretability, evaluation, and theoretical understanding.
- High-Quality and Diverse Generation: Iterative refinement through small denoising steps enables sharp, coherent outputs comparable to GANs, without common GAN instabilities.
- Flexible and Parallelizable Sampling: Recent advances (e.g., DDIM [580]) have accelerated inference significantly, improving practical utility compared to autoregressive and hybrid approaches.
Enrichment 20.9.1: Introduction to Diffusion Models
Diffusion models represent a rigorous class of probabilistic generative models that transform data generation into the problem of reversing a gradual, structured corruption process. Inspired by nonequilibrium thermodynamics [578], these models define a stochastic Markov chain that systematically injects noise into a data sample over many steps—the forward process—until the data is fully randomized. The core learning objective is to parameterize and learn the reverse process: a denoising Markov chain capable of synthesizing realistic data by iteratively refining pure noise back into structured samples. This framework elegantly sidesteps many pitfalls of earlier generative models—such as adversarial collapse in GANs and latent mismatch in VAEs—by relying on explicit, tractable likelihoods and theoretically grounded transitions.
Mathematical Foundation and Dual Processes At the heart of diffusion models are two complementary stochastic processes, each defined with mathematical precision:
-
Forward Process (Diffusion, Corruption):
Let \(\mathbf {x}_0\) be a clean data sample (such as an image). Diffusion-based generative models transform this data into pure noise through a gradual, multi-step corruption process. This is implemented as a Markov chain : \[ \mathbf {x}_0 \rightarrow \mathbf {x}_1 \rightarrow \cdots \rightarrow \mathbf {x}_T, \] where at each timestep \(t\), Gaussian noise is added to slightly degrade the signal. The transition kernel \(q(\mathbf {x}_t \mid \mathbf {x}_{t-1})\) is a probability density function, not a discrete probability. It assigns a scalar density value to a potential noisy state \(\mathbf {x}_t\); a high density indicates that \(\mathbf {x}_t\) is a likely result of adding noise to \(\mathbf {x}_{t-1}\), while a low density implies it is statistically inconsistent with the noise model.
Formally, this transition is defined as a multivariate Gaussian: \begin {equation} q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) = \mathcal {N}\left (\mathbf {x}_t;\, \underbrace {\sqrt {1 - \beta _t} \, \mathbf {x}_{t-1}}_{\mbox{Mean } \boldsymbol {\mu }},\, \underbrace {\beta _t \mathbf {I}}_{\mbox{Covariance } \boldsymbol {\Sigma }} \right ). \label {eq:chapter20_forward_step_detailed} \end {equation} This notation specifies three key components:
- 1.
- Subject (\(\mathbf {x}_t\)): The variable whose likelihood we are measuring.
- 2.
- Mean (\(\boldsymbol {\mu } = \sqrt {1 - \beta _t} \, \mathbf {x}_{t-1}\)): The expected value of the new state. Note that the previous state \(\mathbf {x}_{t-1}\) is scaled down by \(\sqrt {1 - \beta _t}\).
- 3.
- Covariance (\(\boldsymbol {\Sigma } = \beta _t \mathbf {I}\)): The spread of the injected noise, controlled by the scalar \(\beta _t \in (0, 1)\) and the identity matrix \(\mathbf {I}\).
Design Choices: Stability, Structure, and Tractability
The specific mathematical formulation of the forward process is not arbitrary; it relies on careful design choices that ensure the process is stable, computationally tractable, and theoretically sound.
- Why Diagonal Covariance (\(\beta _t \mathbf {I}\))? The covariance term \(\beta _t \mathbf {I}\) signifies that noise is added independently to every pixel (or feature dimension) with equal intensity. The identity matrix \(\mathbf {I}\) ensures zero off-diagonal elements, meaning no spatial correlations are introduced. This is essential because the goal is to degrade structure, not create it; if we used a correlated covariance matrix, we would be effectively painting new, structured patterns onto the image rather than dissolving the original signal into pure noise.
-
Why Variance Preservation? (The Scaling Factor \(\sqrt {1 - \beta _t}\)) One might intuitively assume that to make an image ”noisier”, we should simply add noise on top: \(\mathbf {x}_t = \mathbf {x}_{t-1} + \boldsymbol {\epsilon }\). While this does degrade the image, it increases the total energy of the signal at every step: \[ \mbox{Var}(\mathbf {x}_t) = \mbox{Var}(\mathbf {x}_{t-1}) + \beta _t. \] Repeated over \(T=1000\) steps, the pixel values would explode to huge numbers, causing numerical instability and making neural network training impossible.
Instead, diffusion models are designed to be variance-preserving. We want the distribution of pixel values to stay within a standard dynamic range (e.g., unit variance) throughout the entire process. To achieve this, we must ”make room” for the incoming noise by shrinking the current signal.
The factor \(\sqrt {1 - \beta _t}\) contracts the signal variance exactly enough to counterbalance the added noise variance: \[ \underbrace {\mbox{Var}(\mathbf {x}_t)}_{\approx 1} = \underbrace {(1-\beta _t)\mbox{Var}(\mathbf {x}_{t-1})}_{\mbox{Signal Attenuation}} + \underbrace {\beta _t}_{\mbox{Noise Injection}}. \] Intuition: Imagine mixing a cocktail in a glass of fixed volume. You cannot simply keep adding mixer (noise) to the spirit (signal), or the glass will overflow (exploding variance). Instead, at each step, you pour out a small fraction of the current mixture (attenuation) and top it back up with fresh mixer. By the end, the glass is still full, but the content has transitioned from pure spirit to pure mixer.
This ensures that the final state \(\mathbf {x}_T\) converges to a standard Gaussian \(\mathcal {N}(\mathbf {0}, \mathbf {I})\)—a fixed, well-behaved distribution that serves as a simple starting point for the reverse generation process.
-
Why Gaussian Noise? The choice of a Gaussian kernel is motivated by both physical intuition and mathematical convenience.
- 1.
- Maximum Entropy: For a fixed variance, the Gaussian distribution has the maximum entropy. This means it makes the fewest structural assumptions about the noise, representing ”pure” information loss.
- 2.
- Analytical Tractability: Gaussians possess unique algebraic properties—the product of two Gaussians is a Gaussian, and the convolution of two Gaussians is a Gaussian. This allows us to derive closed-form expressions for the marginals \(q(\mathbf {x}_t \mid \mathbf {x}_0)\) and the posteriors, enabling efficient training without expensive Monte Carlo sampling at every step.
- 3.
- Universality: By the Central Limit Theorem, the sum of many independent noise events tends toward a Gaussian distribution. Thus, modeling the corruption as a sequence of Gaussian steps is a natural approximation for many physical degradation processes.
-
Why a Gradual Multi-Step Process? Why not jump from data to noise in one step (like a VAE) or learn the mapping directly (like a GAN)? The power of diffusion lies in breaking a difficult problem into many easy ones.
Mapping pure noise \(\mathbf {x}_T\) directly to a complex image \(\mathbf {x}_0\) is a highly non-linear and difficult transformation to learn. However, if the steps are small enough (i.e., \(\beta _t\) is small), the reverse transition \(\mathbf {x}_t \to \mathbf {x}_{t-1}\) is a very simple denoising task that can be locally approximated by a Gaussian. This transforms the generative modeling problem from learning one complex map into learning a sequence of simple, stable denoising corrections.
Noise Schedules: How Fast Should the Data Be Destroyed? A crucial design choice in this process is the variance schedule \(\{ \beta _t \}_{t=1}^T\), which controls the pace of corruption. Each \(\beta _t\) determines the noise magnitude at step \(t\): small values preserve structure, while larger values accelerate signal destruction.
One of the earliest and most influential diffusion frameworks, the Denoising Diffusion Probabilistic Model (DDPM) by Ho et al. [223], proposed a simple linear schedule: \[ \beta _t = \mbox{linspace}(10^{-4}, 0.02, T), \] where \(T\) is the total number of diffusion steps (typically 1000). This linear progression ensures that noise is added slowly and evenly, facilitating the learning of the reverse process.
Later works proposed nonlinear schedules to allocate noise more strategically:
- Cosine schedule: Proposed by Nichol and Dhariwal [449], this schedule defines signal decay using a clipped cosine function. It slows down early corruption to preserve information longer and concentrates noise injection toward later steps, improving sample quality.
- Sigmoid or exponential schedules: Other heuristics adopt S-shaped or accelerating curves, delaying heavy corruption until later timesteps to preserve fine details in early latent representations.
The choice of noise schedule significantly affects the signal-to-noise ratio at each step and determines the difficulty of the denoising task.
Figure 20.55: What happens to a distribution in the forward diffusion process? The forward noising process progressively transforms the original data distribution \( q(\mathbf {x}_0) \) into a standard Gaussian \( q(\mathbf {x}_T) \) through a sequence of small Gaussian perturbations. As the noise level increases, intermediate distributions \( q(\mathbf {x}_t) \) become increasingly blurred and entropic, eventually collapsing into an isotropic normal distribution. This transition enables generative modeling by allowing the use of a simple prior at sampling time. Source: Adapted from the CVPR 2022 diffusion models tutorial [582]. Trajectory Properties and Convergence While the step-by-step Gaussian transitions defined in Eq. 20.16 describe the local behavior of the diffusion process, understanding the global behavior of the entire trajectory \(\mathbf {x}_{0:T}\) is essential for both efficient training and theoretical justification.
The Joint Distribution and Markov Property The corruption process is explicitly designed as a Markov chain, meaning the probability of state \(\mathbf {x}_t\) depends solely on the immediate predecessor \(\mathbf {x}_{t-1}\) and not on the earlier history \(\mathbf {x}_{0:t-2}\). This conditional independence assumption allows the joint distribution of the entire forward trajectory to factorize cleanly into a product of local transitions: \begin {equation} \label {eq:chapter20_joint_distribution} q(\mathbf {x}_{1:T} \mid \mathbf {x}_0) = \prod _{t=1}^T q(\mathbf {x}_t \mid \mathbf {x}_{t-1}). \end {equation} This factorization is computationally advantageous: it implies that the complex transformation from data to noise is composed of simple, independent sampling steps, making the process analytically manageable.
Closed-Form Marginals: The ”Shortcut” Property A critical property of Gaussian diffusion is that we do not need to simulate the chain step-by-step to obtain a sample at an arbitrary timestep \(t\). Because the convolution of two Gaussians is another Gaussian, we can derive a closed-form expression for the marginal distribution \(q(\mathbf {x}_t \mid \mathbf {x}_0)\) directly. To simplify the notation, we define the signal retention schedules: \[ \alpha _t := 1 - \beta _t, \qquad \bar {\alpha }_t := \prod _{s=1}^t \alpha _s. \] Here, \(\bar {\alpha }_t\) represents the cumulative signal variance remaining after \(t\) steps. By recursively applying the reparameterization trick \(\mathbf {x}_t = \sqrt {\alpha _t}\mathbf {x}_{t-1} + \sqrt {1-\alpha _t}\boldsymbol {\epsilon }\), we can express \(\mathbf {x}_t\) as a linear combination of the original data \(\mathbf {x}_0\) and a merged noise term: \begin {equation} \label {eq:chapter20_marginal_closed_form} q(\mathbf {x}_t \mid \mathbf {x}_0) = \mathcal {N}\left (\mathbf {x}_t;\, \sqrt {\bar {\alpha }_t} \, \mathbf {x}_0,\, (1 - \bar {\alpha }_t) \mathbf {I} \right ). \end {equation} This identity is fundamental to the efficiency of diffusion models. It allows us to sample training data pairs \((\mathbf {x}_0, \mathbf {x}_t)\) instantly for any \(t\) without running the forward process loop, enabling highly efficient parallel training.
Asymptotic Convergence to Pure Noise The endpoint of the forward process is determined by the limit behavior of \(\bar {\alpha }_t\). For a properly chosen schedule where \(\sum \beta _t \to \infty \), the cumulative signal \(\bar {\alpha }_T\) approaches 0 as \(T \to \infty \). Consequently, the mean \(\sqrt {\bar {\alpha }_T}\mathbf {x}_0\) vanishes, and the variance \((1-\bar {\alpha }_T)\mathbf {I}\) approaches identity: \[ q(\mathbf {x}_T \mid \mathbf {x}_0) \approx \mathcal {N}(\mathbf {0}, \mathbf {I}). \]
This convergence is theoretically grounded in two perspectives:
- 1.
- Central Limit Theorem (CLT): The final noise \(\mathbf {x}_T\) is effectively the sum of many independent, scaled noise injections from previous steps. Even if the local transitions were not perfectly Gaussian, the CLT suggests the cumulative result would tend toward a Gaussian distribution.
- 2.
- Ornstein–Uhlenbeck Process: The discrete steps can be viewed as a discretization of a continuous-time stochastic differential equation (SDE) known as the Ornstein–Uhlenbeck process, which is a mean-reverting process that converges to a stationary Gaussian distribution regardless of the starting state.
This ensures that the generative reverse process can always begin from a standard, easy-to-sample prior \(\mathcal {N}(\mathbf {0}, \mathbf {I})\), decoupled from the complexities of the data distribution.
Preparing for the Reverse Process The properties derived above—stable variance, closed-form marginals, and guaranteed convergence—define a known corruption path that is mathematically invertible. By defining the forward process as a fixed, tractable Markov chain, we create a supervised learning setup: if we know the exact distribution \(q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0)\), we can train a model to approximate it. This paves the path for the reverse process, where the model learns to synthesize realistic data by iteratively denoising pure Gaussian noise.
-
Reverse Process (Denoising, Generation)
The reverse (generative) process in diffusion models starts from pure Gaussian noise, \( \mathbf {x}_T \sim \mathcal {N}(\mathbf {0}, \mathbf {I}) \), and iteratively denoises it into a structured sample \(\mathbf {x}_0\) via a Markov chain: \begin {equation} \mathbf {x}_T \rightarrow \mathbf {x}_{T-1} \rightarrow \cdots \rightarrow \mathbf {x}_0. \label {eq:chapter20_reverse_chain} \end {equation} In an ideal world, each transition would sample from the true reverse conditional \(q(\mathbf {x}_{t-1}\mid \mathbf {x}_t)\). The core difficulty is that this unconditional reverse is not available in closed form for real data.
Why the True Reverse Step \( q(\mathbf {x}_{t-1} \mid \mathbf {x}_t) \) Is Intractable To generate data, we wish to sample from the reverse transition \( q(\mathbf {x}_{t-1} \mid \mathbf {x}_t) \). Let us attempt to derive this distribution analytically using Bayes’ rule. By definition: \begin {equation} \label {eq:chapter20_reverse_bayes} q(\mathbf {x}_{t-1} \mid \mathbf {x}_t) = \frac {q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) \, q(\mathbf {x}_{t-1})}{q(\mathbf {x}_t)}. \end {equation} The first term in the numerator, \( q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) \), is simply the forward diffusion kernel, which is a known Gaussian defined in Eq. 20.16.
However, the calculation breaks down when we examine the marginal probabilities \( q(\mathbf {x}_{t-1}) \) and \( q(\mathbf {x}_t) \). To compute the marginal density of a noisy sample \( \mathbf {x}_t \) , we must integrate over every possible clean image \( \mathbf {x}_0 \) that could have started the chain: \begin {equation} \label {eq:chapter20_marginal_integral} q(\mathbf {x}_t) = \int q(\mathbf {x}_t \mid \mathbf {x}_0) \, \underbrace {q(\mathbf {x}_0)}_{\mbox{Data dist.}} \, d\mathbf {x}_0. \end {equation} Here lies the fundamental problem:
- 1.
- Dependence on the Unknown Data Distribution: The term \( q(\mathbf {x}_0) \) represents the true underlying distribution of natural images (or the specific dataset). This distribution is highly complex, multimodal, and analytically unknown. We do not have a mathematical formula for ”the probability of a picture of a cat”.
- 2.
- Intractable Integration: Because we cannot write down \( q(\mathbf {x}_0) \) in closed form, we cannot perform the integration in Eq. 20.21. Consequently, we cannot calculate the normalization constant \( q(\mathbf {x}_t) \) required for Bayes’ rule.
Intuition: Asking ”What is the previous step given this noisy image?” is equivalent to asking ”Which clean image is this noisy blob most likely to have come from?”. Without knowing the distribution of clean images (the prior), we cannot distinguish between a ”likely” noisy version of a real object and a ”likely” noisy version of random static. Since evaluating the probability of every possible real-world image is impossible, the exact reverse step \( q(\mathbf {x}_{t-1} \mid \mathbf {x}_t) \) remains intractable.
A tractable “teacher” posterior during training During training, we observe the clean data sample \(\mathbf {x}_0 \sim p_{\mbox{data}}\) from the dataset. This distinction is critical: the unconditional reverse transition \(q(\mathbf {x}_{t-1}\mid \mathbf {x}_t)\) is intractable in the data setting because it marginalizes over the unknown data distribution. Concretely, by the law of total probability, \begin {equation} \label {eq:chapter20_intractable_reverse_as_mixture} q(\mathbf {x}_{t-1}\mid \mathbf {x}_t) = \int q(\mathbf {x}_{t-1}\mid \mathbf {x}_t,\mathbf {x}_0)\,q(\mathbf {x}_0\mid \mathbf {x}_t)\,d\mathbf {x}_0. \end {equation} Evaluating this integral would require the posterior \(q(\mathbf {x}_0\mid \mathbf {x}_t)\), which depends on the unknown prior \(p_{\mbox{data}}(\mathbf {x}_0)\) via Bayes’ rule: \(q(\mathbf {x}_0\mid \mathbf {x}_t) \propto q(\mathbf {x}_t\mid \mathbf {x}_0)p_{\mbox{data}}(\mathbf {x}_0)\).
However, if we condition on the specific ground-truth \(\mathbf {x}_0\) used to generate \(\mathbf {x}_t\) during training, the reverse posterior becomes fully analytic: \begin {equation} \label {eq:chapter20_teacher_posterior_def} q(\mathbf {x}_{t-1}\mid \mathbf {x}_t, \mathbf {x}_0). \end {equation} We will treat this tractable posterior as a teacher target: it is the “correct” denoising distribution (under the forward process assumptions) that a neural network (the student) should learn to approximate without access to \(\mathbf {x}_0\) at inference time.
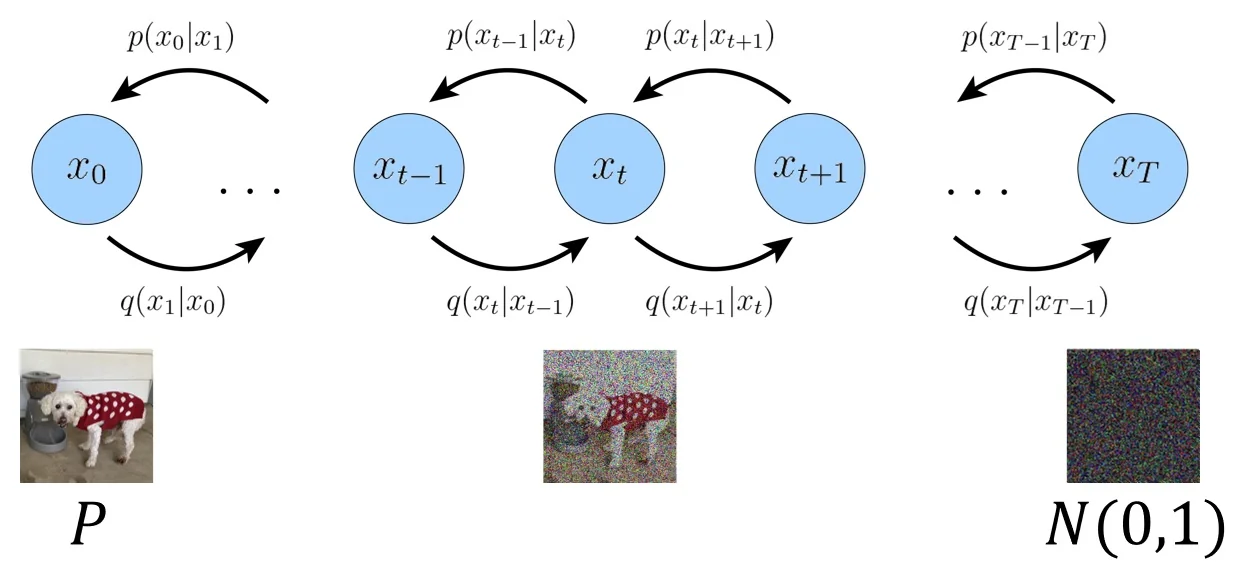
Figure 20.56: Visual intuition for the diffusion process. An input image is progressively corrupted with Gaussian noise over multiple steps (left to right), ultimately yielding pure noise. The learned denoising process (right to left) reverses this trajectory. Conditioning on \(\mathbf {x}_0\) makes the reverse-step posterior \(q(\mathbf {x}_{t-1}\mid \mathbf {x}_t,\mathbf {x}_0)\) a simple Gaussian with closed-form mean and variance, providing an exact training-time target. Adapted from [402]. Derivation of the Posterior \(q(\mathbf {x}_{t-1}\mid \mathbf {x}_t,\mathbf {x}_0)\) We assume the standard DDPM forward process [223, 578]: \begin {equation} \label {eq:chapter20_forward_step} q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) = \mathcal {N}\!\left (\mathbf {x}_t;\, \sqrt {\alpha _t}\,\mathbf {x}_{t-1},\, \beta _t \mathbf {I}\right ), \qquad \alpha _t := 1-\beta _t. \end {equation} Recall the closed-form marginal: \begin {equation} \label {eq:chapter20_forward_marginal_reparam_ref} q(\mathbf {x}_t\mid \mathbf {x}_0) = \mathcal {N}\!\left (\mathbf {x}_t;\, \sqrt {\bar {\alpha }_t}\,\mathbf {x}_0,\,(1-\bar {\alpha }_t)\mathbf {I}\right ), \qquad \bar {\alpha }_t = \prod _{s=1}^t \alpha _s. \end {equation}
Step 1: Bayes’ Rule and the Proportionality Argument
We aim to find the posterior distribution \( q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0) \). Mathematically, we treat \( \mathbf {x}_{t-1} \) as the variable of interest, while \( \mathbf {x}_t \) and \( \mathbf {x}_0 \) are fixed observed values.
Using the definition of conditional probability, we expand the posterior: \begin {equation} \label {eq:chapter20_teacher_posterior_bayes_full} q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0) = \frac {q(\mathbf {x}_t \mid \mathbf {x}_{t-1}, \mathbf {x}_0) \, q(\mathbf {x}_{t-1} \mid \mathbf {x}_0)}{q(\mathbf {x}_t \mid \mathbf {x}_0)}. \end {equation} First, we apply the Markov property to the first term in the numerator. Given the immediate past \( \mathbf {x}_{t-1} \), the future state \( \mathbf {x}_t \) depends only on the noise added at that step and is independent of the distant past \( \mathbf {x}_0 \). Thus, \( q(\mathbf {x}_t \mid \mathbf {x}_{t-1}, \mathbf {x}_0) \) simplifies to \( q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) \).
Second, consider the denominator, \( q(\mathbf {x}_t \mid \mathbf {x}_0) \). Notice that this term depends only on \( \mathbf {x}_t \) and \( \mathbf {x}_0 \). Crucially, it does not contain the variable \( \mathbf {x}_{t-1} \). From the perspective of a function over \( \mathbf {x}_{t-1} \), the denominator is merely a constant scaling factor (often denoted as \( Z \) or \( C \)). In Gaussian derivation, it is standard practice to ignore such normalization constants and focus on the functional form (or kernel) of the distribution. If we can show that the exponent is quadratic in \( \mathbf {x}_{t-1} \), we define the distribution as Gaussian and calculate the normalization later (or infer it from the variance).
Therefore, we replace the equality with a proportionality sign (\( \propto \)), retaining only the terms that shape the distribution of \( \mathbf {x}_{t-1} \): \begin {equation} \label {eq:chapter20_posterior_product} q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0) \propto \underbrace {q(\mathbf {x}_t \mid \mathbf {x}_{t-1})}_{\mbox{Likelihood (Forward Step)}} \cdot \underbrace {q(\mathbf {x}_{t-1} \mid \mathbf {x}_0)}_{\mbox{Prior (Marginal)}}. \end {equation}
Step 2: Analyzing the Gaussian Factors
We now define the explicit forms of these two factors using the forward process definitions.
1. The Prior Term (Marginal): This is the distribution of \( \mathbf {x}_{t-1} \) given the starting data \( \mathbf {x}_0 \). From the closed-form marginal property, we know: \begin {equation} \label {eq:chapter20_prior_xtm1_given_x0} q(\mathbf {x}_{t-1} \mid \mathbf {x}_0) = \mathcal {N}\left (\mathbf {x}_{t-1};\, \sqrt {\bar {\alpha }_{t-1}}\mathbf {x}_0,\; (1-\bar {\alpha }_{t-1})\mathbf {I}\right ), \end {equation} where \( \bar {\alpha }_{t-1} = \prod _{s=1}^{t-1} (1-\beta _s) \) is the cumulative signal variance.
2. The Likelihood Term (Transition): The forward transition is defined as a conditional distribution over the next step \( \mathbf {x}_t \): \[ q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) = \mathcal {N}(\mathbf {x}_t; \sqrt {\alpha _t}\mathbf {x}_{t-1}, \beta _t\mathbf {I}), \quad \mbox{where } \alpha _t = 1 - \beta _t. \] To combine this with the prior (a distribution over \( \mathbf {x}_{t-1} \)), we need to multiply them. Since the prior is a function of \( \mathbf {x}_{t-1} \), it is mathematically convenient to also view this likelihood term as a function of \( \mathbf {x}_{t-1} \) (treating \( \mathbf {x}_t \) as a fixed observation).
Detailed Derivation: Inverting the Gaussian View Recall that the probability density function (PDF) of a Gaussian \( \mathcal {N}(\mathbf {y}; \boldsymbol {\mu }, \sigma ^2\mathbf {I}) \) is determined entirely by the term inside its exponent: \[ p(\mathbf {y}) \propto \exp \left ( -\frac {1}{2\sigma ^2} \|\mathbf {y} - \boldsymbol {\mu }\|^2 \right ). \] Any expression we can rearrange into the form \( \exp ( -\frac {1}{2C} \|\mathbf {x} - \mathbf {m}\|^2 ) \) implies a Gaussian distribution over \( \mathbf {x} \) with mean \( \mathbf {m} \) and variance \( C \).
Let us analyze the exponent of \( q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) \): \[ E = -\frac {1}{2\beta _t} \|\mathbf {x}_t - \sqrt {\alpha _t}\mathbf {x}_{t-1}\|^2. \] Our goal is to isolate \( \mathbf {x}_{t-1} \) so that it looks like \( \|\mathbf {x}_{t-1} - \dots \|^2 \).
- 1.
- Symmetry of the Norm: The squared Euclidean distance is symmetric (\( \|a-b\|^2 = \|b-a\|^2 \)). We swap the terms to put our variable of interest, \( \mathbf {x}_{t-1} \), first: \[ \|\mathbf {x}_t - \sqrt {\alpha _t}\mathbf {x}_{t-1}\|^2 = \|\sqrt {\alpha _t}\mathbf {x}_{t-1} - \mathbf {x}_t\|^2. \]
- 2.
- Factoring out the Scalar: We want the coefficient of \( \mathbf {x}_{t-1} \) to be 1. We factor \( \sqrt {\alpha _t} \) out of the vector subtraction inside the norm: \[ \sqrt {\alpha _t}\mathbf {x}_{t-1} - \mathbf {x}_t = \sqrt {\alpha _t} \left ( \mathbf {x}_{t-1} - \frac {1}{\sqrt {\alpha _t}}\mathbf {x}_t \right ). \]
- 3.
- Squaring the Factor: Recall the norm property \( \|c \cdot \mathbf {v}\|^2 = c^2 \|\mathbf {v}\|^2 \). When we pull \( \sqrt {\alpha _t} \) outside the squared norm, it becomes \( (\sqrt {\alpha _t})^2 = \alpha _t \): \[ \left \| \sqrt {\alpha _t} \left ( \mathbf {x}_{t-1} - \frac {1}{\sqrt {\alpha _t}}\mathbf {x}_t \right ) \right \|^2 = \alpha _t \left \| \mathbf {x}_{t-1} - \frac {1}{\sqrt {\alpha _t}}\mathbf {x}_t \right \|^2. \]
- 4.
- Substituting Back: Now we plug this transformed norm back into the original exponential expression: \[ \exp (E) = \exp \left ( -\frac {1}{2\beta _t} \cdot \alpha _t \left \| \mathbf {x}_{t-1} - \frac {1}{\sqrt {\alpha _t}}\mathbf {x}_t \right \|^2 \right ). \]
- 5.
- Identifying Variance: We group the scalars to match the standard Gaussian form \( -\frac {1}{2\sigma ^2} \). \[ -\frac {\alpha _t}{2\beta _t} = -\frac {1}{2 (\beta _t / \alpha _t)}. \] This identifies the effective variance \( \sigma ^2 \) as \( \frac {\beta _t}{\alpha _t} \).
Conclusion: The functional form with respect to \( \mathbf {x}_{t-1} \) is: \[ \exp \left ( -\frac {1}{2 (\frac {\beta _t}{\alpha _t})} \left \| \mathbf {x}_{t-1} - \frac {1}{\sqrt {\alpha _t}}\mathbf {x}_t \right \|^2 \right ). \] By inspection, this is proportional to a Gaussian density with:
- Mean: \( \frac {1}{\sqrt {\alpha _t}}\mathbf {x}_t \) (the observed next step, scaled backwards).
- Variance: \( \frac {\beta _t}{\alpha _t}\mathbf {I} \) (the forward noise scaled by the inverse signal factor).
Thus, we write the proportionality: \begin {equation} \label {eq:chapter20_likelihood_as_gaussian_in_xtm1} q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) \propto \mathcal {N}\left (\mathbf {x}_{t-1};\, \frac {1}{\sqrt {\alpha _t}}\mathbf {x}_t,\; \frac {\beta _t}{\alpha _t}\mathbf {I}\right ). \end {equation}
Step 3: Calculating Posterior Precision and Mean
We now multiply the two Gaussians derived above. The product of two Gaussians \( \mathcal {N}(\boldsymbol {\mu }_1, \boldsymbol {\Sigma }_1) \) and \( \mathcal {N}(\boldsymbol {\mu }_2, \boldsymbol {\Sigma }_2) \) is a new Gaussian \( \mathcal {N}(\tilde {\boldsymbol {\mu }}, \tilde {\boldsymbol {\Sigma }}) \), where the precisions (inverse variances) add: \begin {equation} \label {eq:chapter20_gaussian_product_identity} \tilde {\boldsymbol {\Sigma }}^{-1} = \boldsymbol {\Sigma }_1^{-1} + \boldsymbol {\Sigma }_2^{-1}, \qquad \tilde {\boldsymbol {\mu }} = \tilde {\boldsymbol {\Sigma }} \left ( \boldsymbol {\Sigma }_1^{-1}\boldsymbol {\mu }_1 + \boldsymbol {\Sigma }_2^{-1}\boldsymbol {\mu }_2 \right ). \end {equation} Substituting our specific variances \( \boldsymbol {\Sigma }_1 = \frac {\beta _t}{\alpha _t}\mathbf {I} \) and \( \boldsymbol {\Sigma }_2 = (1-\bar {\alpha }_{t-1})\mathbf {I} \):
\begin {equation} \label {eq:chapter20_posterior_precision_calc} \tilde {\beta }_t^{-1} \mathbf {I} = \left ( \frac {\alpha _t}{\beta _t} + \frac {1}{1-\bar {\alpha }_{t-1}} \right ) \mathbf {I} = \left ( \frac {\alpha _t(1-\bar {\alpha }_{t-1}) + \beta _t}{\beta _t(1-\bar {\alpha }_{t-1})} \right ) \mathbf {I}. \end {equation} Using the identity \( \bar {\alpha }_t = \alpha _t \bar {\alpha }_{t-1} \) and \( \beta _t = 1 - \alpha _t \), the numerator simplifies to \( 1 - \bar {\alpha }_t \). Inverting the result gives the closed-form posterior variance: \begin {equation} \label {eq:chapter20_posterior_variance} \tilde {\beta }_t = \frac {1-\bar {\alpha }_{t-1}}{1-\bar {\alpha }_t} \beta _t. \end {equation} Similarly, computing the weighted mean yields: \begin {equation} \label {eq:chapter20_posterior_mean_closedform} \tilde {\boldsymbol {\mu }}_t(\mathbf {x}_t, \mathbf {x}_0) = \frac {\sqrt {\bar {\alpha }_{t-1}}\beta _t}{1-\bar {\alpha }_t}\mathbf {x}_0 + \frac {\sqrt {\alpha _t}(1-\bar {\alpha }_{t-1})}{1-\bar {\alpha }_t}\mathbf {x}_t. \end {equation} This gives us the final tractable distribution \( q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0) = \mathcal {N}(\tilde {\boldsymbol {\mu }}_t, \tilde {\beta }_t \mathbf {I}) \), which acts as the target for our neural network.
Reparameterizing the Posterior via Noise Prediction While the closed-form expression for the posterior mean \(\tilde {\boldsymbol {\mu }}_t(\mathbf {x}_t, \mathbf {x}_0)\) derived in Eq. (20.33) is mathematically exact, it presents a practical difficulty: it depends explicitly on the clean image \(\mathbf {x}_0\). At inference time, \(\mathbf {x}_0\) is exactly what we are trying to generate and is therefore unknown. To make this posterior useful for a generative model, we must re-express it in terms of quantities available to the network.
Recall the reparameterization of the forward marginal \(q(\mathbf {x}_t \mid \mathbf {x}_0)\), which relates the noisy state \(\mathbf {x}_t\) to the clean data \(\mathbf {x}_0\) and the cumulative noise \(\boldsymbol {\epsilon }\): \[ \mathbf {x}_t = \sqrt {\bar {\alpha }_t}\mathbf {x}_0 + \sqrt {1-\bar {\alpha }_t}\boldsymbol {\epsilon }, \quad \mbox{where } \boldsymbol {\epsilon } \sim \mathcal {N}(\mathbf {0}, \mathbf {I}). \] We can invert this relationship to express the unknown \(\mathbf {x}_0\) as a function of the current noisy state \(\mathbf {x}_t\) and the noise vector \(\boldsymbol {\epsilon }\): \[ \mathbf {x}_0 = \frac {\mathbf {x}_t - \sqrt {1-\bar {\alpha }_t}\boldsymbol {\epsilon }}{\sqrt {\bar {\alpha }_t}}. \] Substituting this expression back into the formula for the posterior mean \(\tilde {\boldsymbol {\mu }}_t\) (Eq. (20.33)) allows us to eliminate \(\mathbf {x}_0\). After algebraic simplification, we arrive at an implementation-critical identity that depends only on \(\mathbf {x}_t\) and \(\boldsymbol {\epsilon }\): \begin {equation} \label {eq:chapter20_posterior_mean_eps_form} \tilde {\boldsymbol {\mu }}_t(\mathbf {x}_t, \mathbf {x}_0) = \frac {1}{\sqrt {\alpha _t}} \left ( \mathbf {x}_t - \frac {\beta _t}{\sqrt {1-\bar {\alpha }_t}}\,\boldsymbol {\epsilon } \right ). \end {equation} Key Insight: This equation reveals that the optimal denoising step is just a scaled version of the input \(\mathbf {x}_t\) minus a scaled version of the noise \(\boldsymbol {\epsilon }\). Since \(\mathbf {x}_t\) is known at the current step, the only unknown quantity required to compute the optimal reverse trajectory is the noise \(\boldsymbol {\epsilon }\) itself. Therefore, learning to approximate the posterior mean is mathematically equivalent to learning to predict the noise present in the image.
Teacher–Student Learning: Matching the Posterior To perform generation, we introduce a learnable “student” model \(p_\theta \) designed to approximate the true time-reversed process. Since the true posterior \(q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0)\) is Gaussian, we parameterize the student transition also as a Gaussian: \begin {equation} \label {eq:chapter20_student_reverse_gaussian} p_\theta (\mathbf {x}_{t-1} \mid \mathbf {x}_t) = \mathcal {N}\!\left (\mathbf {x}_{t-1};\,\boldsymbol {\mu }_\theta (\mathbf {x}_t,t),\,\sigma _t^2\mathbf {I}\right ). \end {equation} Here, \(\boldsymbol {\mu }_\theta \) is a neural network (typically a U-Net) that predicts the mean of the next state, and \(\sigma _t^2\) is the variance (often set to a fixed schedule such as \(\beta _t\) or \(\tilde {\beta }_t\)).
We train this model using a Teacher–Student framework. During training, we have access to the ground truth data, so the exact posterior \(q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0)\) (the “teacher”) is computable. We optimize the student parameters \(\theta \) to match the teacher by minimizing the Kullback-Leibler (KL) divergence at every timestep: \begin {equation} \label {eq:chapter20_teacher_student_kl} \mathcal {L}_t(\theta ) = \mathrm {KL}\!\left ( q(\mathbf {x}_{t-1}\mid \mathbf {x}_t,\mathbf {x}_0) \;\|\; p_\theta (\mathbf {x}_{t-1}\mid \mathbf {x}_t) \right ). \end {equation} Because the KL divergence between two Gaussians is dominated by the squared Euclidean distance between their means, minimizing this objective is equivalent (up to scaling factors) to minimizing the Mean Squared Error (MSE) between the teacher’s mean \(\tilde {\boldsymbol {\mu }}_t\) and the student’s predicted mean \(\boldsymbol {\mu }_\theta \).
The Noise-Prediction Objective Leveraging the insight from Eq. (20.34), we parameterize the student network not to predict the mean directly, but to predict the noise \(\boldsymbol {\epsilon }\). We define the network output \(\boldsymbol {\epsilon }_\theta (\mathbf {x}_t, t)\) and construct the mean prediction as: \begin {equation} \label {eq:chapter20_mu_theta_from_eps} \boldsymbol {\mu }_\theta (\mathbf {x}_t,t) := \frac {1}{\sqrt {\alpha _t}} \left ( \mathbf {x}_t - \frac {\beta _t}{\sqrt {1-\bar {\alpha }_t}}\,\boldsymbol {\epsilon }_\theta (\mathbf {x}_t,t) \right ). \end {equation} By substituting this parameterization into the KL divergence objective, the loss function simplifies significantly. The complicated coefficients describing the mean collapse into a single time-dependent weight, and the target becomes simply the true noise vector \(\boldsymbol {\epsilon }\) sampled during the forward process: \begin {equation} \label {eq:chapter20_eps_mse_weighted} \mathcal {L}_t(\theta ) = \mathbb {E}_{\mathbf {x}_0,\boldsymbol {\epsilon }}\!\left [ \lambda _t \;\big \|\boldsymbol {\epsilon } - \boldsymbol {\epsilon }_\theta (\mathbf {x}_t, t)\big \|_2^2 \right ], \quad \mbox{where } \lambda _t = \frac {\beta _t^2}{2\sigma _t^2 \alpha _t (1-\bar {\alpha }_t)}. \end {equation} This result is profound: complex generative modeling is reduced to a sequence of denoising autoencoder tasks. The network simply learns to look at a noisy image \(\mathbf {x}_t\) and estimate the noise \(\boldsymbol {\epsilon }\) that corrupted it.
Theoretical Justification: The Variational Lower Bound (ELBO) One might ask: is matching the posterior at each step strictly equivalent to maximizing the likelihood of the generated data? The answer is yes, provided we consider the entire trajectory.
The local teacher–student objectives \(\mathcal {L}_t\) arise naturally from maximizing the Evidence Lower Bound (ELBO) on the log-likelihood \(\log p_\theta (\mathbf {x}_0)\). Just as in VAEs, where we optimize a bound on the marginal likelihood of the data, diffusion models optimize a bound derived from the joint distribution of the forward and reverse chains: \begin {equation} \label {eq:chapter20_elbo_decomposition_general} \log p_\theta (\mathbf {x}_0) \ge \mathcal {L}_{\mathrm {ELBO}} = \mathbb {E}_{q}\left [ \log \frac {p_\theta (\mathbf {x}_{0:T})}{q(\mathbf {x}_{1:T} \mid \mathbf {x}_0)} \right ]. \end {equation} When expanded, this global objective decomposes into a sum of local terms corresponding exactly to the objectives we derived heuristically: \begin {equation} \label {eq:chapter20_elbo_decomposition_explicit} \mathcal {L}_{\mathrm {ELBO}} = \underbrace {-\,\mathrm {KL}(q(\mathbf {x}_T|\mathbf {x}_0)\,\|\,p(\mathbf {x}_T))}_{\mbox{Prior Matching}} \;-\; \sum _{t=2}^T \underbrace {\mathbb {E}_{q}\!\left [\mathrm {KL}(q(\mathbf {x}_{t-1}|\mathbf {x}_t,\mathbf {x}_0)\,\|\,p_\theta (\mathbf {x}_{t-1}|\mathbf {x}_t))\right ]}_{\mbox{Denoising Matching (Teacher-Student)}} \;+\; \underbrace {\mathbb {E}_{q}\!\left [\log p_\theta (\mathbf {x}_0|\mathbf {x}_1)\right ]}_{\mbox{Reconstruction}}. \end {equation} This decomposition proves that by training the model to match the teacher posterior (denoising matching) and ensuring the final latent matches the prior (prior matching), we are mathematically maximizing the likelihood of the generated data.
In the following section, we will explore the specific algorithm that instantiates this framework—the Denoising Diffusion Probabilistic Model (DDPM)—and detail the practical simplifications, such as discarding the weighting term \(\lambda _t\), that lead to a practical diffusion approach for image generation.
Enrichment 20.9.2: Denoising Diffusion Probabilistic Models (DDPM)
Denoising Diffusion Probabilistic Models (DDPM) [223] represent a seminal advance in the development of practical and highly effective diffusion-based generative models. DDPMs distill the general diffusion modeling framework into a concrete, efficient, and empirically powerful algorithm for image synthesis—transforming the theoretical appeal of diffusion into state-of-the-art results on real data.
Enrichment 20.9.2.1: Summary of Core Variables in Diffusion Models
Purpose and Motivation Before deriving the ELBO-based training objective of DDPMs, it is critical to clearly understand the set of variables and coefficients that structure both the forward and reverse processes. The loss function ultimately minimized in DDPMs is derived from the KL divergence between a true posterior and a learned reverse process. Both of these distributions depend intimately on Gaussian means and variances computed using scalar quantities such as \( \beta _t \), \( \alpha _t \), \( \bar {\alpha }_t \), and \( \tilde {\beta }_t \). Without explicitly recalling what these mean—and how they interact—the derivation of the objective risks becoming opaque or unmotivated.
Practical Implementation: Reverse Variance and Sampling While the mean \(\boldsymbol {\mu }_\theta (\mathbf {x}_t, t)\) is learned via the noise prediction objective, the reverse process variance \(\sigma _t^2\) must also be defined to perform sampling.
1. Choices for Reverse Variance \( \sigma _t^2 \) The full reverse transition is
\( p_\theta (\mathbf {x}_{t-1} \mid \mathbf {x}_t) = \mathcal {N}(\mathbf {x}_{t-1};\, \boldsymbol {\mu }_\theta (\mathbf {x}_t, t),\, \sigma _t^2 \mathbf {I}) \). Two common strategies exist for setting \(\sigma _t^2\):
- Posterior-matching (\( \sigma _t^2 = \tilde {\beta }_t \)): Sets the variance to the true posterior variance derived in Eq. (20.32). This aligns the model with the theoretical reverse process and is analytically precise.
- Forward-matching (\( \sigma _t^2 = \beta _t \)): Sets the variance to the forward noise schedule. This is often empirically stable and simpler to implement. Ideally, \(\tilde {\beta }_t \approx \beta _t\) when sampling steps are small, making them interchangeable in practice [223].
2. The Role of Stochasticity (Why Inject Noise?) The sampling update rule is: \[ \mathbf {x}_{t-1} = \boldsymbol {\mu }_\theta (\mathbf {x}_t, t) + \sigma _t \mathbf {z}, \quad \mbox{where } \mathbf {z} \sim \mathcal {N}(\mathbf {0}, \mathbf {I}). \] Why do we add the random noise term \(\sigma _t \mathbf {z}\) instead of just taking the predicted mean?
- Generative Diversity: The noise injection ensures the process remains stochastic. It allows the model to generate multiple distinct outputs \(\mathbf {x}_0\) from the same starting noise \(\mathbf {x}_T\), exploring the full diversity of the data distribution.
- Correcting Errors: Without noise, the process would collapse into a deterministic trajectory that might drift off the data manifold. The noise corrects small errors in the mean prediction, keeping the trajectory “fuzzy” enough to land in a valid high-probability region.
Note: In the final step (\(t=1\)), noise is typically omitted (\(\mathbf {z}=\mathbf {0}\)) to output the best clean estimate without adding residual grain.
Intuitive Summary of Core Variables To navigate the derivation and implementation of diffusion models, it is essential to build a strong intuition for the four scalar schedules and tensor quantities that govern the process. We summarize them here as functional components of the generative engine:
- The Corruption Schedule (\( \beta _t \)): Controls the rate of information destruction. A small \( \beta _t \) implies a gentle diffusion step where image structure is preserved, whereas a large \( \beta _t \) represents aggressive corruption. The schedule \( \{ \beta _t \}_{t=1}^T \) is monotonically increasing to ensure data is slowly dissolved into noise rather than destroyed abruptly [223].
- Cumulative Signal Health (\( \bar {\alpha }_t \)): Quantifies the remaining signal strength of \( \mathbf {x}_0 \) inside the noisy state \( \mathbf {x}_t \). Defined as \( \prod _{s=1}^t (1-\beta _s) \), it acts as a “signal-to-noise” ratio indicator. When \( \bar {\alpha }_t \approx 1 \) (early \( t \)), the sample is pristine; when \( \bar {\alpha }_t \to 0 \) (late \( t \)), the sample is effectively pure Gaussian noise. This scalar allows us to jump directly to any timestep during training without simulating intermediate steps.
- The Ideal Reverse Target (\( \tilde {\boldsymbol {\mu }}_t \)): Represents the optimal denoising destination. If we had access to the ground truth \( \mathbf {x}_0 \), \( \tilde {\boldsymbol {\mu }}_t \) is exactly where we should move \( \mathbf {x}_t \) to optimally reverse the last noise injection. It is a weighted blend of the noisy observation (what we see) and the clean signal (what we know). Training essentially forces the model to guess this target without seeing \( \mathbf {x}_0 \).
- The Learned Gradient (\( \boldsymbol {\epsilon }_\theta \)): The engine of generation. Instead of predicting the image directly, the network estimates the noise vector pointing “away” from the data manifold. Subtracting this estimated noise from \( \mathbf {x}_t \) (scaled appropriately) pushes the sample effectively “towards” the clean data distribution, approximating the score function (gradient of the log-density).
Enrichment 20.9.2.2: ELBO Formulation and Loss Decomposition
Maximum Likelihood with a Latent Diffusion Trajectory A DDPM functions as a latent-variable generative model, but with a distinct structure: its latent variables are the sequence of intermediate noisy states \(\mathbf {x}_{1:T}\) rather than a single compressed vector. Notably, each latent \(\mathbf {x}_t \in \mathbb {R}^D\) maintains the same dimensionality as the input data \(\mathbf {x}_0 \in \mathbb {R}^D\).
The generative process is defined as a reverse Markov chain that
begins with pure noise \(\mathbf {x}_T\) and progressively removes it to synthesize data: \begin {equation} \label {eq:chapter20_reverse_chain_joint} p_\theta (\mathbf {x}_{0:T}) = p(\mathbf {x}_T)\prod _{t=1}^{T} p_\theta (\mathbf {x}_{t-1}\mid \mathbf {x}_t), \qquad p(\mathbf {x}_T)=\mathcal {N}(\mathbf {0},\mathbf {I}). \end {equation}
Here, each transition \(p_\theta (\mathbf {x}_{t-1}\mid \mathbf {x}_t)\) is typically modeled as a time-conditional Gaussian
\( \mathcal {N}(\mathbf {x}_{t-1}; \boldsymbol {\mu }_\theta (\mathbf {x}_t, t), \boldsymbol {\Sigma }_\theta (t)) \), where the mean is parameterized by a neural network.
Training this model by maximum likelihood requires optimizing the marginal log-likelihood of the observed data \(\mathbf {x}_0\): \begin {equation} \label {eq:chapter20_marginal_likelihood_integral} \log p_\theta (\mathbf {x}_0) = \log \int p_\theta (\mathbf {x}_{0:T})\, d\mathbf {x}_{1:T}. \end {equation} This integral necessitates marginalizing over all possible high-dimensional trajectories \(\mathbf {x}_{1:T}\) that could have collapsed into \(\mathbf {x}_0\). Due to the depth of the chain (\(T \approx 1000\)) and the complex, learned nature of the reverse transitions, this computation is analytically intractable.
Introducing the Forward Process as a Variational Distribution To obtain a tractable objective, we introduce an auxiliary distribution \(q(\mathbf {x}_{1:T}\mid \mathbf {x}_0)\) and apply variational inference. In diffusion models, the key design choice is to set \(q\) to the fixed forward noising process [223, 578]: \begin {equation} \label {eq:chapter20_forward_chain} q(\mathbf {x}_{1:T}\mid \mathbf {x}_0)=\prod _{t=1}^T q(\mathbf {x}_t\mid \mathbf {x}_{t-1}), \qquad q(\mathbf {x}_t\mid \mathbf {x}_{t-1}) = \mathcal {N}\!\left (\mathbf {x}_t;\sqrt {\alpha _t}\mathbf {x}_{t-1},\beta _t\mathbf {I}\right ). \end {equation} This distribution is defined by a fixed noise schedule \(\beta _t\in (0,1)\) and \(\alpha _t:=1-\beta _t\). Because each transition is Gaussian, \(q(\mathbf {x}_{1:T}\mid \mathbf {x}_0)\) spans the entire space \(\mathbb {R}^{DT}\), ensuring that the log-ratios in the objective are well-defined for any possible trajectory.
From the “Missing Integral” to a Tractable Expectation To make the marginal likelihood \( \log p_\theta (\mathbf {x}_0) \) computable, we transform the integration problem into an expectation problem. We multiply and divide the term inside the integral by our chosen variational distribution \(q(\mathbf {x}_{1:T}\mid \mathbf {x}_0)\): \begin {align} \log p_\theta (\mathbf {x}_0) &= \log \int q(\mathbf {x}_{1:T}\mid \mathbf {x}_0)\, \frac {p_\theta (\mathbf {x}_{0:T})}{q(\mathbf {x}_{1:T}\mid \mathbf {x}_0)}\, d\mathbf {x}_{1:T} \label {eq:chapter20_importance_identity}\\ &= \log \mathbb {E}_{q(\mathbf {x}_{1:T}\mid \mathbf {x}_0)} \left [ \frac {p_\theta (\mathbf {x}_{0:T})}{q(\mathbf {x}_{1:T}\mid \mathbf {x}_0)} \right ]. \label {eq:chapter20_expectation_form} \end {align}
Why is this transformation useful? The move from Eq. (20.21) to Eq. (20.21) leverages the definition of the expected value: \(\mathbb {E}_q[f(\mathbf {x})] \equiv \int q(\mathbf {x})f(\mathbf {x}) d\mathbf {x}\). While the original integral requires evaluating all possible noise trajectories (an infinite and intractable set), the expectation form allows us to use Monte Carlo estimation.
Instead of analytically solving the integral, we can approximate the expectation by sampling a single trajectory \(\mathbf {x}_{1:T}\) from the forward process \(q\). Since \(q\) is a fixed Gaussian Markov chain, generating these samples is computationally trivial. This transforms the problem from impossible high-dimensional integration to simple stochastic sampling.
Jensen’s Inequality and the ELBO Because \(\log \) is concave, Jensen’s inequality (\(\log \mathbb {E}[X] \ge \mathbb {E}[\log X]\)) gives a lower bound: \begin {align} \log p_\theta (\mathbf {x}_0) &\ge \mathbb {E}_{q(\mathbf {x}_{1:T}\mid \mathbf {x}_0)} \left [ \log \frac {p_\theta (\mathbf {x}_{0:T})}{q(\mathbf {x}_{1:T}\mid \mathbf {x}_0)} \right ] =: \mathcal {L}_{\mathrm {ELBO}}(\theta ;\mathbf {x}_0). \label {eq:chapter20_elbo_definition} \end {align}
Maximizing \(\mathcal {L}_{\mathrm {ELBO}}\) is therefore a principled surrogate for maximizing \(\log p_\theta (\mathbf {x}_0)\).
Expanding the ELBO: Products Become Sums Substituting the Markov factorizations from Eqs. (20.41)–(20.43) into Eq. (20.41) and using \(\log \prod _t a_t=\sum _t\log a_t\) yields \begin {align} \mathcal {L}_{\mathrm {ELBO}}(\theta ;\mathbf {x}_0) = \mathbb {E}_{q} \Big [ \log p(\mathbf {x}_T) + \sum _{t=1}^{T}\log p_\theta (\mathbf {x}_{t-1}\mid \mathbf {x}_t) - \sum _{t=1}^{T}\log q(\mathbf {x}_t\mid \mathbf {x}_{t-1}) \Big ], \label {eq:chapter20_elbo_expanded_raw} \end {align}
where \(q\) is shorthand for \(q(\mathbf {x}_{1:T}\mid \mathbf {x}_0)\). This form is correct but not yet aligned with the backward-time conditionals that will appear in KL divergences.
The Posterior Trick: Aligning the Forward and Reverse Directions We face a structural mismatch in the ELBO derived so far (Eq. (20.1)). The ELBO contains a sum of forward transitions \(\log q(\mathbf {x}_t \mid \mathbf {x}_{t-1})\), which describe the diffusion process going forward in time. However, our generative model \(p_\theta (\mathbf {x}_{t-1} \mid \mathbf {x}_t)\) operates backward in time. To define a meaningful loss function (like a KL divergence), we must compare distributions that define the same transition direction (\(t \to t-1\)).
To fix this, we do not ”solve” for an unknown; rather, we use Bayes’ rule to rewrite the forward term \(\log q(\mathbf {x}_t \mid \mathbf {x}_{t-1})\) into an equivalent expression involving the reverse posterior.
1. Inverting the arrow with Bayes’ Rule
Recall that for the Markov chain conditioned on \(\mathbf {x}_0\), the reverse posterior is defined
as: \[ q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0) = \frac {q(\mathbf {x}_t \mid \mathbf {x}_{t-1}, \mathbf {x}_0) \, q(\mathbf {x}_{t-1} \mid \mathbf {x}_0)}{q(\mathbf {x}_t \mid \mathbf {x}_0)}. \] Using the Markov property \(q(\mathbf {x}_t \mid \mathbf {x}_{t-1}, \mathbf {x}_0) = q(\mathbf {x}_t \mid \mathbf {x}_{t-1})\), we can rearrange this identity to isolate the
forward term found in our ELBO: \begin {equation} \label {eq:chapter20_bayes_identity_telescoping} \log q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) = \underbrace {\log q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0)}_{\mbox{Aligned Reverse Posterior}} + \underbrace {\log q(\mathbf {x}_t \mid \mathbf {x}_0) - \log q(\mathbf {x}_{t-1} \mid \mathbf {x}_0)}_{\mbox{Normalization Constants}}. \end {equation} Why do this? We have successfully replaced
a term pointing ”forward” (which we cannot compare to \(p_\theta \)) with a term
pointing ”backward” (which we can compare to \(p_\theta \)) plus some residual
marginals.
2. The Telescoping Sum
When we sum this substitution over all timesteps \(t=2 \dots T\), the residual marginal terms
cancel each other out in a cascading (telescoping) series: \begin {align} \sum _{t=2}^{T} \left [ \log q(\mathbf {x}_t|\mathbf {x}_0) - \log q(\mathbf {x}_{t-1}|\mathbf {x}_0) \right ] &= (\log q(\mathbf {x}_2|\mathbf {x}_0) - \log q(\mathbf {x}_1|\mathbf {x}_0)) \nonumber \\ &\quad + (\log q(\mathbf {x}_3|\mathbf {x}_0) - \log q(\mathbf {x}_2|\mathbf {x}_0)) \nonumber \\ &\quad + \dots \nonumber \\ &\quad + (\log q(\mathbf {x}_T|\mathbf {x}_0) - \log q(\mathbf {x}_{T-1}|\mathbf {x}_0)) \nonumber \\ &= \log q(\mathbf {x}_T \mid \mathbf {x}_0) - \log q(\mathbf {x}_1 \mid \mathbf {x}_0). \label {eq:chapter20_telescoping_cancellation} \end {align}
This effectively removes all intermediate marginals from the loss function. When we combine this result with the \(t=1\) term from the original sum, the final expression simplifies to just the sum of reverse posteriors plus the endpoint at \(T\): \begin {equation} \label {eq:chapter20_forward_sum_rewritten} \sum _{t=1}^{T} \log q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) = \sum _{t=2}^{T} \log q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0) + \log q(\mathbf {x}_T \mid \mathbf {x}_0). \end {equation}
ELBO Decomposition into the Standard DDPM Terms We now consolidate the terms to reveal the final objective. Recall our starting point: the expanded ELBO from Eq. (20.1). \[ \mathcal {L}_{\mathrm {ELBO}} = \mathbb {E}_{q(\mathbf {x}_{1:T} \mid \mathbf {x}_0)} \Bigg [ \log p(\mathbf {x}_T) + \sum _{t=1}^T \log p_\theta (\mathbf {x}_{t-1} \mid \mathbf {x}_t) - \sum _{t=1}^T \log q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) \Bigg ]. \]
The Obstacle (Direction Mismatch): We want to train the reverse model \( p_\theta (\mathbf {x}_{t-1} \mid \mathbf {x}_t) \). Ideally, we would minimize a distance (like KL divergence) between this model and some ground truth. However, the ELBO currently contains the forward terms \( \log q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) \). These point in the wrong direction (time \( t-1 \to t \)). We cannot directly compare a forward transition \( q \) to a reverse transition \( p_\theta \). To fix this, we must replace the forward sum with terms that point backwards in time.
Step 1: Applying the Telescoping Substitution
We substitute the forward sum using the telescoping identity derived in
Eq. (20.45): \[ \sum _{t=1}^{T} \log q(\mathbf {x}_t \mid \mathbf {x}_{t-1}) = \log q(\mathbf {x}_T \mid \mathbf {x}_0) + \sum _{t=2}^{T} \log q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0). \] Notice that the terms inside the sum, \( q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0) \), now point backwards
(from \( t \) to \( t-1 \)), conditioned on \( \mathbf {x}_0 \). This aligns perfectly with our generative model
\( p_\theta (\mathbf {x}_{t-1} \mid \mathbf {x}_t) \).
Step 2: Regrouping the ELBO
Substituting this back into the ELBO and grouping matching terms (prior with
prior, transition with transition): \begin {align} \mathcal {L}_{\mathrm {ELBO}} = \mathbb {E}_{q(\mathbf {x}_{1:T} \mid \mathbf {x}_0)} \Bigg [ &\underbrace {\log p_\theta (\mathbf {x}_0 \mid \mathbf {x}_1)}_{\text {Reconstruction } (t=1)} \nonumber \\ + &\underbrace {\left ( \log p(\mathbf {x}_T) - \log q(\mathbf {x}_T \mid \mathbf {x}_0) \right )}_{\text {Prior Matching } (t=T)} \nonumber \\ + &\sum _{t=2}^{T} \underbrace {\left ( \log p_\theta (\mathbf {x}_{t-1} \mid \mathbf {x}_t) - \log q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0) \right )}_{\text {Denoising Matching } (t=2 \dots T)} \Bigg ]. \end {align}
Step 3: From Global Expectation to Local KLs
The expectation \( \mathbb {E}_{q(\mathbf {x}_{1:T} \mid \mathbf {x}_0)} \) is an integral over the entire trajectory. However, each grouped
term depends on only a few variables. We can simplify the expectations by
marginalizing out the irrelevant variables.
- Prior Term: Depends only on \( \mathbf {x}_T \). \[ \mathbb {E}_{q(\mathbf {x}_{1:T} \mid \mathbf {x}_0)} \left [ \log \frac {p(\mathbf {x}_T)}{q(\mathbf {x}_T \mid \mathbf {x}_0)} \right ] = \mathbb {E}_{q(\mathbf {x}_T \mid \mathbf {x}_0)} \left [ \log \frac {p(\mathbf {x}_T)}{q(\mathbf {x}_T \mid \mathbf {x}_0)} \right ] = -\mathrm {KL}(q(\mathbf {x}_T \mid \mathbf {x}_0) \,\|\, p(\mathbf {x}_T)). \]
- Denoising Terms (\(t>1\)): The term at step \( t \) depends on \( \mathbf {x}_t \) and \( \mathbf {x}_{t-1} \). We can split the expectation using the chain rule \( q(\mathbf {x}_t, \mathbf {x}_{t-1} \mid \mathbf {x}_0) = q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0) q(\mathbf {x}_t \mid \mathbf {x}_0) \): \[ \mathbb {E}_{q(\mathbf {x}_{1:T} \mid \mathbf {x}_0)} \left [ \dots \right ] = \mathbb {E}_{q(\mathbf {x}_t \mid \mathbf {x}_0)} \Bigg [ \underbrace {\mathbb {E}_{q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0)} \left [ \log \frac {p_\theta (\mathbf {x}_{t-1} \mid \mathbf {x}_t)}{q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0)} \right ]}_{-\mathrm {KL}(q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0) \,\|\, p_\theta (\mathbf {x}_{t-1} \mid \mathbf {x}_t))} \Bigg ]. \] The inner expectation is exactly the negative KL divergence between the posterior and the model. The outer expectation averages this KL over all possible noise levels \( \mathbf {x}_t \) sampled from \( q(\mathbf {x}_t \mid \mathbf {x}_0) \).
The Standard Variational Bound Decomposition We customarily minimize the negative ELBO (denoted \( L \)). Combining the results above yields the canonical decomposition from the DDPM paper [223]: \begin {equation} \label {eq:chapter20_vlb_decomp_L_terms} L = \underbrace {L_0}_{\mbox{Reconstruction}} + \underbrace {L_T}_{\mbox{Prior Matching}} + \sum _{t=2}^{T} \underbrace {L_{t-1}}_{\mbox{Denoising Matching}}, \end {equation} where the individual loss terms are defined as: \begin {align} L_0 &:= -\log p_\theta (\mathbf {x}_0 \mid \mathbf {x}_1), \label {eq:chapter20_L0_def}\\ L_T &:= \mathrm {KL}(q(\mathbf {x}_T \mid \mathbf {x}_0) \,\|\, p(\mathbf {x}_T)), \label {eq:chapter20_LT_def}\\ L_{t-1} &:= \mathbb {E}_{q(\mathbf {x}_t \mid \mathbf {x}_0)} \Big [ \mathrm {KL}(q(\mathbf {x}_{t-1} \mid \mathbf {x}_t, \mathbf {x}_0) \,\|\, p_\theta (\mathbf {x}_{t-1} \mid \mathbf {x}_t)) \Big ]. \label {eq:chapter20_Lt_def} \end {align}
Why is this powerful? Because we chose Gaussian transitions for both the forward process \( q \) and the reverse model \( p_\theta \), every KL divergence inside \( L_T \) and \( L_{t-1} \) can be computed in closed form. This avoids high-variance Monte Carlo estimates for the KL terms themselves. We only need to sample the outer expectation \( \mathbb {E}_{q(\mathbf {x}_t \mid \mathbf {x}_0)} \), which is efficiently handled by sampling a single \( \mathbf {x}_t \) during each training step.
Interpretation: What Each Term Is Doing (and What Actually Trains \(\theta \)) Eq. (20.46) isolates exactly where learning happens:
- Stepwise denoising KLs \(\mathcal {L}_{t-1}\) (the main trainable supervision). For each \(t\ge 2\), the model transition \(p_\theta (\mathbf {x}_{t-1}\mid \mathbf {x}_t)\) is trained to match the true posterior \(q(\mathbf {x}_{t-1}\mid \mathbf {x}_t,\mathbf {x}_0)\) induced by the forward process. This is the core “analytic teacher / learned student” mechanism: during training \(\mathbf {x}_0\) is known, so the teacher posterior is tractable; at sampling time \(\mathbf {x}_0\) is unknown, so only \(p_\theta \) remains.
- Prior KL \(\mathcal {L}_T\) (typically \(\theta \)-independent). With a fixed forward schedule and fixed prior \(p(\mathbf {x}_T)\), \(\mathcal {L}_T\) depends only on \(q\) and \(p\), and contributes no gradient to \(\theta \). Conceptually, it accounts for matching the endpoint distribution of the forward chain to the chosen prior.
- Decoder / reconstruction \(\mathcal {L}_0\). This term trains the final step mapping a lightly noised \(\mathbf {x}_1\) back to data \(\mathbf {x}_0\). It plays the same role as a VAE decoder likelihood term: its exact form is an implementation choice (e.g., a discretized Gaussian when \(\mathbf {x}_0\) is integer-valued pixel data).
Why This Matters for Implementation This decomposition is not a heuristic: it is the variational identity that converts an intractable marginal likelihood objective into a sum of tractable per-timestep losses. In practice, we estimate these expectations by sampling a minibatch \(\mathbf {x}_0\), drawing a timestep \(t\), sampling \(\mathbf {x}_t\sim q(\mathbf {x}_t\mid \mathbf {x}_0)\), and evaluating the corresponding term. Once we choose a parameterization of the reverse Gaussian mean (e.g., predicting \(\boldsymbol {\epsilon }\) or \(\mathbf {x}_0\)), the denoising KLs \(\mathcal {L}_{t-1}\) reduce (up to \(\theta \)-independent constants and known timestep-dependent weights) to the simple regression objectives used in modern implementations [223, 449].
Enrichment 20.9.2.3: Training and Inference in DDPMs
Denoising diffusion probabilistic models (DDPMs) learn to reverse a fixed, gradually destructive noise process. The forward process perturbs a clean sample \( x_0 \) by injecting Gaussian noise over \( T \) steps, transforming it into a nearly pure noise vector \( x_T \). The model is trained to invert this process: starting from \( x_T \sim \mathcal {N}(0, \mathbb {I}) \), it denoises step-by-step, ideally recovering a sample on the data manifold.
Training Phase. Instead of directly reconstructing the clean image \( x_0 \), the model is trained to predict the exact noise \( \varepsilon \sim \mathcal {N}(0, \mathbb {I}) \) used to generate a corrupted sample \( x_t \) at a randomly selected timestep. This is done using the closed-form reparameterization: \[ x_t = \sqrt {\bar {\alpha }_t} \, x_0 + \sqrt {1 - \bar {\alpha }_t} \, \varepsilon . \]
This formula defines the marginal distribution \( q(x_t \mid x_0) \), which is analytically tractable because the forward process adds Gaussian noise at each step. Thanks to the Gaussian structure, we can bypass the full Markov chain \( x_0 \to x_1 \to \dots \to x_t \) and sample \( x_t \) directly from \( x_0 \). Since \( x_0 \) is available during training, we know both the corrupted image \( x_t \) and the noise \( \varepsilon \) used to produce it — giving us a clean, fully supervised learning signal at every step.
A new timestep \( t \sim \mathrm {Uniform}(1, T) \) is sampled independently for each training example in every iteration. This stochastic scheduling ensures that the model is exposed evenly to all levels of noise — from lightly perturbed images (\( t \) small) to highly corrupted ones (\( t \) large). As a result, the network learns to denoise across the entire corruption spectrum, handling both subtle and extreme distortions.
Crucially, the model is not trained to perform full denoising in a single step. Rather, it learns a local denoising direction at a specific timestep — the vector that reduces the noise level just slightly. These local predictions are later chained together during inference, gradually converting pure noise \( x_T \sim \mathcal {N}(0, \mathbb {I}) \) into a coherent image. In this way, the global generative trajectory is composed of small, timestep-specific updates, each learned with direct supervision.
The objective is a simple mean squared error: \[ \mathcal {L}_\theta (t) = \left \| \varepsilon - \varepsilon _\theta (x_t, t) \right \|^2, \] where \( \varepsilon _\theta \) is the model’s noise estimate given the noisy input and timestep. Because \( \varepsilon \sim \mathcal {N}(0, \mathbb {I}) \) has a time-invariant distribution, this formulation provides uniformly scaled gradients and avoids timestep-dependent loss reweighting.
- Sample minibatch \( \{x_0^{(i)}\}_{i=1}^B \sim q(x_0) \)
- For each sample, draw \( t \sim \mathrm {Uniform}(\{1, \dots , T\}) \)
- Sample \( \varepsilon \sim \mathcal {N}(0, \mathbb {I}) \)
- Generate corrupted input: \[ x_t = \sqrt {\bar {\alpha }_t} \, x_0 + \sqrt {1 - \bar {\alpha }_t} \, \varepsilon \]
- Update \( \theta \) by minimizing: \[ \frac {1}{B} \sum _{i=1}^B \left \| \varepsilon ^{(i)} - \varepsilon _\theta (x_t^{(i)}, t^{(i)}) \right \|^2 \]
Sampling Phase. Once training is complete, DDPMs generate new data by sampling from the learned reverse process. The generative trajectory begins with a latent \( x_T \sim \mathcal {N}(0, \mathbb {I}) \) and iteratively denoises it using the model’s predictions until a final sample \( x_0 \) is obtained.
Connection to the Model Distribution \( p_\theta (x_{t-1} \mid x_t) \). During inference, each reverse step samples from a parameterized Gaussian: \[ p_\theta (x_{t-1} \mid x_t) = \mathcal {N}\left (x_{t-1};\, \mu _\theta (x_t, t),\, \sigma _t^2 \mathbb {I} \right ), \] where the mean \( \mu _\theta (x_t, t) \) is derived from the model’s noise prediction: \[ \mu _\theta (x_t, t) = \frac {1}{\sqrt {\alpha _t}} \left ( x_t - \frac {1 - \alpha _t}{\sqrt {1 - \bar {\alpha }_t}} \cdot \varepsilon _\theta (x_t, t) \right ), \] and \( \sigma _t^2 \) is either fixed (e.g., set to the posterior variance \( \tilde {\beta }_t \)) or learned.
Interpreting the Update. This formula is a direct consequence of substituting the predicted noise into the reparameterized form of the posterior mean. Intuitively, the model estimates the direction that locally increases the probability density of the data at each step — a learned score-like vector pointing toward higher likelihood under the evolving distribution \( p_t(x_t) \).
Stochasticity and Sample Diversity. The added noise \( \sigma _t z \), where \( z \sim \mathcal {N}(0, \mathbb {I}) \), ensures that the process remains stochastic for all \( t > 1 \). This stochasticity is crucial for generating diverse outputs: even with a fixed starting point \( x_T \), the sampled trajectory may differ based on the random noise added at each step, enabling the model to explore multiple valid reconstructions from the same latent seed.
Final Step Refinement. To ensure a clean and stable output, the final step at \( t = 1 \) is typically performed deterministically: \[ x_0 = \mu _\theta (x_1, 1) = \frac {1}{\sqrt {\alpha _1}} \left ( x_1 - \frac {1 - \alpha _1}{\sqrt {1 - \bar {\alpha }_1}} \cdot \varepsilon _\theta (x_1, 1) \right ). \] This prevents reintroducing noise into the final output and produces the model’s best estimate of a sample from the data distribution.
- Initialize \( x_T \sim \mathcal {N}(0, \mathbb {I}) \)
-
For \( t = T, \dots , 1 \):
- If \( t > 1 \), sample \( z \sim \mathcal {N}(0, \mathbb {I}) \); else set \( z = 0 \)
- Compute: \[ x_{t-1} = \mu _\theta (x_t, t) + \sigma _t z \]
- Return final sample \( x_0 \)
Each step applies the learned mean \( \mu _\theta (x_t, t) \) and injects a calibrated amount of noise \( \sigma _t z \), gradually transforming white noise into a structured output. This aligns training and sampling: the same noise prediction \( \varepsilon _\theta (x_t, t) \) used in the objective is used here to parameterize \( p_\theta (x_{t-1} \mid x_t) \), ensuring behavioral consistency and high-fidelity synthesis.
Enrichment 20.9.2.4: Architecture, Datasets, and Implementation Details
Backbone Architecture: Why U-Net Fits Denoising in Diffusion Models At the heart of Denoising Diffusion Probabilistic Models (DDPMs) is the noise prediction network \( \varepsilon _\theta (x_t, t) \), which learns to estimate the additive Gaussian noise present in a noisy image \( x_t \) at a given diffusion timestep \( t \). The model’s objective is not to directly recover the clean image \( x_0 \), but to predict the noise \( \varepsilon \) that was added to it—a simpler and more stable residual formulation that exploits the additive structure of the forward process.
In nearly all implementations, this network adopts a modernized U-Net architecture [532], an encoder–decoder design with skip connections. Originally introduced for biomedical image segmentation, U-Net embodies architectural principles that are highly compatible with denoising: multiscale abstraction, spatial alignment preservation, and residual refinement. For foundational architectural background, refer to §15.6.
Why an Encoder–Decoder? Even though the goal is to produce an output of the same shape as the input—namely, a per-pixel noise estimate \( \hat {\varepsilon }_\theta (x_t, t) \in \mathbb {R}^{H \times W \times C} \)—a plain convolutional stack is inadequate. To accurately predict structured noise, the model must:
- Understand global layout and semantic structure, which is necessary at high noise levels.
- Recover fine-grained spatial details and local noise textures, which dominate at low noise levels.
The encoder–decoder design serves precisely this purpose. The encoder compresses the input into an abstract, low-resolution representation that captures global context. The decoder then expands this representation back to full resolution, guided by high-resolution activations passed through skip connections. This configuration allows the model to infer both where and how much noise is present across scales, producing a high-fidelity noise map to subtract from \( x_t \), yielding the denoised estimate \( x_{t-1} \).
Multiscale Hierarchy and Architectural Intuition The forward diffusion process corrupts an image gradually and hierarchically: fine textures and high-frequency details vanish early in the process, while coarse shapes and global structure persist longer but are eventually lost as the timestep increases. The U-Net mirrors this hierarchy in its encoder–decoder structure, enabling effective prediction of structured noise across all scales.
- Encoder (Global Noise Pattern Extractor): The encoder consists of convolutional and residual blocks, each followed by downsampling via strided convolutions or pooling. These stages progressively reduce spatial resolution and increase the receptive field. As a result, the encoder extracts increasingly abstract features that capture global noise patterns—broad, low-frequency components of the corruption that dominate at high noise levels (large \( t \)). These features help the model reason about the type and spatial layout of large-scale noise.
-
Bottleneck (Compressed Noise Signature): At the coarsest resolution, the bottleneck fuses information across the entire image. It often includes attention layers to model long-range dependencies, forming a compact semantic summary of the noise. Rather than focusing on local details, this stage encodes a global noise signature that allows the model to estimate how structured or unstructured the corruption is throughout the image.
- Decoder (Localized Noise Detail Refiner): The decoder reverses the downsampling process by progressively upsampling the bottleneck features back to the original resolution. At each scale, upsampled features are concatenated with the corresponding encoder outputs through skip connections, enabling the model to reconstruct the spatial pattern of the noise with pixel-level precision. This is especially important at small \( t \), where most signal remains and the model must predict subtle residual noise components for fine denoising.
- Skip Connections (High-Fidelity Noise Anchors): These direct links transmit high-resolution features from the encoder to the decoder, bypassing the lossy bottleneck. They preserve local structure from the input \( x_t \) and act as spatial anchors, helping the model retain and refine localized noise patterns without needing to regenerate them from coarse representations. In essence, skip connections allow the decoder to focus on correcting residual noise at each pixel, not reconstructing structure from scratch.
This architectural design aligns naturally with the multiscale nature of the denoising task. The encoder and bottleneck guide the model at early timesteps (large \( t \)), when noise dominates and global structure must be inferred. The decoder and skip connections specialize in late timesteps (small \( t \)), where fine details are visible and precise noise subtraction is required.
Walkthrough: Layer-by-Layer Data Flow A DDPM U-Net processes its input as follows:
- 1.
- Input: A noisy image \( x_t \in \mathbb {R}^{H \times W \times C} \) and scalar timestep \( t \) are provided.
- 2.
- Timestep Embedding: The timestep is encoded via sinusoidal or learned embeddings, then added to or modulates each residual block throughout the network. This enables conditional denoising behavior based on the current noise level.
- 3.
- Encoder Path: Residual blocks compress the spatial resolution stage-by-stage while enriching the semantic representation. Intermediate activations are stored for later skip connections.
- 4.
- Bottleneck: A central residual block—often augmented with self-attention—integrates global context across the latent space.
- 5.
- Decoder Path: Each upsampling stage increases spatial resolution and concatenates the corresponding encoder feature map. Residual blocks then refine the merged features.
- 6.
- Output Projection: A final convolution reduces the output channels to match the input image dimensions, producing the predicted noise map \( \hat {\varepsilon }_\theta (x_t, t) \in \mathbb {R}^{H \times W \times C} \).
Why U-Net Matches the Diffusion Objective The U-Net is ideally suited to the demands of iterative denoising:
- At high \( t \), the model must infer missing structure from context—enabled by the encoder and bottleneck’s large receptive field.
- At low \( t \), it must restore subtle noise patterns and textures—achieved through decoder refinement and skip connections.
- The model’s residual nature matches the objective of DDPMs: instead of “generating from nothing,” it incrementally removes noise, learning what to subtract.
This architectural symmetry between noise corruption and hierarchical reconstruction makes U-Net a natural backbone for DDPMs, explaining its ubiquity in both pixel-space and latent-space diffusion models.
Resolution and Depth Scaling The model scales its architecture to accommodate input resolution. This adjustment is often described as a resolution–depth tradeoff: deeper U-Nets are used for higher-resolution datasets to ensure that the receptive field covers the full image, while shallower variants suffice for low-resolution images:
- CIFAR-10 (\( 32 \times 32 \)): Uses 4 resolution levels, downsampling by factors of 2 from \( 32 \times 32 \to 4 \times 4 \).
- LSUN, CelebA-HQ (\( 256 \times 256 \)): Use 6 resolution levels, down to \( 4 \times 4 \), which allows deeper processing and more extensive multi-scale aggregation.
This scaling ensures a balance between global context (captured at coarser resolutions) and fine-grained detail (preserved by skip connections and upsampling paths), and prevents over- or under-modeling at different scales.
Time Embedding via Sinusoidal Positional Encoding Each diffusion step is associated with a timestep index \( t \in \{1, \dots , T\} \), which determines the noise level in the corrupted image \( x_t \). Rather than inputting \( t \) directly as a scalar or spatial channel, DDPMs encode this index using a sinusoidal positional embedding, as introduced in the Transformer architecture [644]. For details, see Section §17.
The embedding maps \( t \) to a high-dimensional vector: \[ \mbox{Embed}(t)[2i] = \sin \left ( \frac {t}{10000^{2i/d}} \right ), \quad \mbox{Embed}(t)[2i+1] = \cos \left ( \frac {t}{10000^{2i/d}} \right ), \] where \( d \) is the embedding dimension. This yields a rich multi-scale representation of \( t \) that provides smooth variation and relative ordering across timesteps.
How the Time Embedding is Used The sinusoidal vector \( \mbox{Embed}(t) \in \mathbb {R}^d \) is passed through a small multilayer perceptron (MLP), typically a two-layer feedforward network with a nonlinearity (e.g., SiLU). The output of the MLP is a transformed time embedding \( \tau \in \mathbb {R}^{d'} \) where \( d' \) matches the number of feature channels in the current resolution level of the network.
This transformed vector \( \tau \) is then used as follows:
- In each residual block of the U-Net, \( \tau \) is broadcast across the spatial dimensions and added to the activations before the first convolution: \[ h \leftarrow h + \mbox{Broadcast}(\tau ), \] where \( h \in \mathbb {R}^{C \times H \times W} \) is the intermediate feature map and \( \mbox{Broadcast}(\tau ) \in \mathbb {R}^{C \times H \times W} \) repeats \( \tau \) across spatial locations.
- This additive conditioning modulates the computation in every block with timestep-specific information, allowing the network to adapt its filters and responses to the level of corruption in \( x_t \).
- The time embedding is reused across multiple resolution levels and is injected consistently at all depths of the U-Net.
Why Not Simpler Alternatives? Several naive strategies for injecting time \( t \) into the network fail to match the effectiveness of sinusoidal embeddings:
- Feeding \( t \) as a scalar input: Adding a scalar value lacks expressivity and does not capture periodicity or multi-scale structure in the diffusion process.
- Concatenating \( t \) as a spatial channel: Appending a constant-valued image channel representing \( t \) adds no location-specific structure and forces the network to learn to decode the meaning of the timestep from scratch, which is inefficient and unprincipled.
- Learned timestep embeddings: While possible, they tend to overfit to the training schedule. In contrast, sinusoidal embeddings are fixed and continuous, allowing generalization to unseen timesteps or schedules.
Hence, sinusoidal positional encoding provides a continuous, high-capacity representation of the timestep index \( t \), and its integration into every residual block ensures the network remains temporally aware throughout the forward pass. This architectural choice is central to DDPMs’ ability to generalize across the full noise schedule and to specialize behavior for early vs. late denoising stages.
Model Scale and Dataset Diversity DDPMs have been shown to scale effectively across a range of standard image generation benchmarks, with model capacity adjusted to match dataset complexity and resolution. The success of diffusion models across these diverse datasets underscores their flexibility and robustness for modeling natural image distributions:
- CIFAR-10: A \( 32 \times 32 \) low-resolution dataset of natural images across 10 object categories (e.g., airplanes, frogs, trucks). The DDPM trained on CIFAR-10 uses a relatively compact architecture with 35.7 million parameters.
- LSUN (Bedrooms, Churches): High-resolution (\( 256 \times 256 \)) scene-centric datasets focused on structured indoor and outdoor environments. These demand greater capacity to model texture, lighting, and geometry. DDPMs trained on LSUN use 114 million-parameter models.
- CelebA-HQ: A curated set of high-resolution (\( 256 \times 256 \)) face images with fine details in skin, hair, and expression. The model architecture is the same as for LSUN, with 114 million parameters.
- Large LSUN Bedroom Variant: To push fidelity further, a 256 million-parameter model is trained by increasing the number of feature channels. This variant improves texture quality and global coherence in challenging scene synthesis.
Together, these results demonstrate that DDPMs can successfully generate images across a variety of domains—ranging from small-object classification datasets to high-resolution indoor scenes and human faces—by appropriately scaling model depth and width to meet data complexity.
Summary In summary, the DDPM network combines a modernized U-Net backbone with residual connections, attention, group normalization, and sinusoidal time embeddings to robustly model the denoising process at all noise levels. These design choices reflect a convergence of innovations from generative modeling, deep CNNs, and sequence-based architectures, resulting in a stable and expressive architecture well-suited for diffusion-based generation.
Enrichment 20.9.2.5: Empirical Evaluation and Latent-Space Behavior
Noise Prediction Yields Stable Training and Best Sample Quality The DDPM training objective can be formulated in multiple ways — most notably by regressing the true posterior mean \( \tilde {\mu }_t \), the original image \( x_0 \), or the noise \( \varepsilon \) used to corrupt the data. An ablation from [223] highlights the empirical advantage of predicting \( \varepsilon \), especially when using the simplified loss: \[ \mathcal {L}_{\mbox{simple}}(\theta ) = \mathbb {E}_{x_0, \varepsilon , t} \left \| \varepsilon - \varepsilon _\theta (x_t, t) \right \|^2. \]
In Table 2 of the original paper, DDPMs trained to directly predict noise and using a fixed isotropic variance achieve a FID score of 3.17 on CIFAR-10, outperforming all other parameterizations. Notably:
- Mean prediction with fixed variance reaches FID \(13.22\), but training with learned variance is unstable.
- Noise prediction stabilizes training and achieves state-of-the-art performance.
Image Interpolation in Latent Space Interpolating images in pixel space typically leads to distorted, unrealistic samples. However, interpolating in the diffusion latent space allows for smooth transitions while maintaining realism.
Let \( x_0, x_0' \sim p(x_0) \) be two real samples and define their noised versions \( x_t \sim q(x_t \mid x_0) \) and \( x_t' \sim q(x_t' \mid x_0') \). Interpolation in pixel space between \( x_0 \) and \( x_0' \) yields low-quality results, as such mixtures are not on the data manifold.
Instead, the DDPM first encodes both inputs into latent noise space via the forward process. It then linearly interpolates the latent pair: \[ \bar {x}_t = (1 - \lambda ) x_t + \lambda x_t', \] and decodes this interpolated noise via the learned denoising process: \[ \bar {x}_0 \sim p_\theta (x_0 \mid \bar {x}_t). \]
The results are realistic samples that blend semantic attributes from both source images — such as hairstyle, pose, and identity features. The rec columns (i.e., \( \lambda = 0 \) and \( \lambda = 1 \)) show faithful reconstructions of \( x_0 \) and \( x_0' \), confirming that the process remains semantically grounded.
Coarse-to-Fine Interpolation and Structural Completion Unlike the previous interpolation experiment — where two images were encoded to the same noise level \( t \) and interpolated under varying weights \( \lambda \) — this experiment investigates a different axis of generative control: the impact of interpolating at different diffusion depths.
The idea is to fix two source images \( x_0, x_0' \sim p(x_0) \), encode them to different levels of corruption \( x_t, x_t' \), perform latent-space interpolation as before: \[ \bar {x}_t = (1 - \lambda ) x_t + \lambda x_t', \] and decode \( \bar {x}_t \sim p_\theta (x_0 \mid \bar {x}_t) \) via DDPM. But here, the timestep \( t \) itself is varied to control the granularity of information being destroyed and recombined.
As shown in Figure 20.58, we observe:
- \( t = 0 \): Interpolation occurs directly in pixel space. The resulting images are unrealistic and far off-manifold, suffering from blurry blends and unnatural artifacts.
- \( t = 250 \): Fine-grained attributes (like expression, or hair texture) blend smoothly, but core identity remains distinct.
- \( t = 750 \): High-level semantic traits such as pose, facial structure, and lighting are interpolated. The model effectively recombines partial semantic cues from both images.
- \( t = 1000 \): The forward diffusion has fully erased both source images. The interpolated latent lies near the prior, and the reverse process generates novel samples that do not resemble either input — underscoring the destructive nature of high \( t \).
This experiment demonstrates that the forward diffusion process acts as a tunable semantic bottleneck. Small \( t \) values retain local details, enabling fine-grained morphing, while large \( t \) values eliminate low-level information, allowing the model to semantically complete or reinvent samples during denoising. Crucially, it reveals how diffusion models naturally support interpolation at different abstraction levels — from texture to structure — within a single framework.
Progressive Lossy Compression via Reverse Denoising Beyond interpolation, DDPMs enable an elegant form of semantic compression. By encoding images to a latent \( x_t \) via forward diffusion and decoding with \( p_\theta (x_0 \mid x_t) \), one can interpret \( x_t \) as a progressively degraded version of the original — retaining coarse structure at high \( t \), and finer details at lower \( t \).
Figure 20.59 illustrates this behavior by fixing a latent \( x_t \) from a given source image and sampling multiple reconstructions at different noise levels. We observe:
- High \( t \) (e.g., 1000): Almost all detail is destroyed. Yet, all samples from \( p_\theta (x_0 \mid x_t) \) consistently reflect global properties such as face orientation and head shape — traits that persist deep into the diffusion process.
- Intermediate \( t \) (e.g., 750): Mid-level features like sunglasses, skin tone, or background begin to reemerge — attributes not present at \( t = 1000 \), but encoded in the intermediate latent.
- Low \( t \) (e.g., 500): Fine texture and local details (e.g., wrinkles, clothing patterns, eye sharpness) are reconstructed. The samples are perceptually similar and show near-lossless decoding.
This complements the earlier latent interpolation experiments: while Figure 20.57 and Figure 20.58 showed how DDPMs mix image content by interpolating between latents, Figure 20.59 focuses on what semantic content is recoverable from a given latent. Together, these experiments reveal that:
- The forward process acts as a progressive semantic bottleneck — discarding detail layer by layer, akin to a lossy compression encoder.
- The reverse process serves as a generative decoder, robustly reconstructing from incomplete information while respecting semantic priors.
- DDPMs naturally support multiple levels of abstraction — from global pose to pixel-level texture — controllable by the timestep \( t \).
Critically, these findings also validate the choice of noise prediction and fixed-variance reverse transitions (as shown in the ablation table): DDPMs not only achieve strong FID scores but exhibit robust, controllable behavior across a range of generation and compression tasks — without the need for external encoders or separate latent spaces.
Enrichment 20.9.3: Denoising Diffusion Implicit Models (DDIM)
Motivation While DDPMs produce high-quality samples, their sampling procedure is slow: generating each image requires thousands of iterative steps, each injecting noise and resampling from a Gaussian. Denoising Diffusion Implicit Models (DDIM) [580] propose a faster, possibly deterministic (depending on our choice), alternative that reuses the noise trajectory learned during DDPM training. Thus, allowing fewer, non-randomized reverse steps — without retraining the model.
The DDIM construction hinges on the forward diffusion process and its reparameterization, offering a principled method to interpolate or skip timesteps using the same noise that corrupted the clean sample. This enables sparse, deterministic or stochastic generation, with controllable speed and sample diversity.
From DDPM Sampling to DDIM Inversion To understand DDIM, we begin by revisiting a key property of the forward diffusion in DDPMs: the fact that it admits a closed-form Gaussian marginal at each timestep \( t \), conditioned on the original sample \( x_0 \). This allows any noisy sample \( x_t \) to be written deterministically in terms of \( x_0 \) and a latent noise variable \( \varepsilon \).
Importantly, this deterministic reparameterization can be inverted if we have access to \( x_t \) and the corresponding noise \( \varepsilon \). DDIM leverages this observation by proposing a new reverse sampling mechanism: instead of sampling \( x_{t-1} \sim p_\theta (x_{t-1} \mid x_t) \) using stochastic transitions, DDIM deterministically reconstructs a denoised signal estimate \( \hat {x}_0 \), then reuses the same noise to compute \( x_s \) for some \( s < t \), bypassing the need for Gaussian resampling.
The result is a non-Markovian, deterministic sampling trajectory defined entirely by the model’s noise prediction \( \varepsilon _\theta (x_t, t) \), which acts as a proxy for the latent variable governing the entire diffusion path. This insight allows DDIM to:
- Reconstruct \( x_0 \) from a noisy \( x_t \) using a single inference pass.
- Reuse the predicted noise to deterministically compute earlier samples \( x_s \).
- Support arbitrary skip steps and non-uniform timestep schedules.
- Eliminate stochasticity from the reverse process (optionally reintroducing it with a tunable variance, to enhance the outputs variety).
We now derive the DDIM reverse (denoising) formula by walking through each conceptual and mathematical step.
1. From Forward Diffusion to Inversion The DDPM forward process defines a tractable Gaussian marginal at each timestep: \[ q(x_t \mid x_0) = \mathcal {N}\left ( \sqrt {\bar {\alpha }_t} \, x_0,\, (1 - \bar {\alpha }_t) \, \mathbb {I} \right ), \] which admits the following reparameterization: \[ x_t = \sqrt {\bar {\alpha }_t} \, x_0 + \sqrt {1 - \bar {\alpha }_t} \, \varepsilon , \qquad \varepsilon \sim \mathcal {N}(0, \mathbb {I}). \]
This expression shows that \( x_t \) lies on a deterministic path defined by the clean sample \( x_0 \) and the noise variable \( \varepsilon \). If both \( x_t \) and \( \varepsilon \) are known, we can recover the original sample using: \[ x_0 = \frac {1}{\sqrt {\bar {\alpha }_t}} \left ( x_t - \sqrt {1 - \bar {\alpha }_t} \cdot \varepsilon \right ). \]
However, during sampling, we only observe the noisy sample \( x_t \). The clean image \( x_0 \) is unknown. To address this, the model is trained to approximate the injected noise: \[ \varepsilon \approx \varepsilon _\theta (x_t, t), \] allowing us to estimate the clean sample as: \[ \hat {x}_0 = \frac {1}{\sqrt {\bar {\alpha }_t}} \left ( x_t - \sqrt {1 - \bar {\alpha }_t} \cdot \varepsilon _\theta (x_t, t) \right ). \]
This single-step estimate \( \hat {x}_0 \) may be inaccurate when \( t \) is large — that is, when \( x_t \) is heavily corrupted by noise and the denoising task is most difficult. Hence, DDIM continues with a multi-step procedure: starting from pure noise \( x_T \), it progressively refines samples \( x_t, \dots x_{s<t}, \dots , x_0 \) using noise prediction and noise reuse. We now derive the mechanism that enables this recursive denoising.
2. Reverse Step to Arbitrary \( s < t \) In DDPM, the reverse process is modeled as a Markov chain: \[ x_T \rightarrow x_{T-1} \rightarrow x_{T-2} \rightarrow \dots \rightarrow x_0, \] where each step involves sampling from a Gaussian distribution conditioned only on the previous timestep. This formulation requires a long sequence of small, incremental denoising updates — typically 1000 steps — to reach high-quality samples.
DDIM generalizes this by allowing non-Markovian jumps: it permits transitions from any timestep \( x_t \) to any earlier timestep \( x_s \) (with \( s < t \)), skipping over intermediate states. This defines a shortened inference path of the form: \[ x_T \rightarrow x_{t_1} \rightarrow x_{t_2} \rightarrow \dots \rightarrow x_0, \] with \( T > t_1 > t_2 > \dots > 0 \), often using just 25, 50, or 100 steps — significantly accelerating sampling.
This is possible because DDIM leverages the closed-form marginals of the forward process: \[ x_s = \sqrt {\bar {\alpha }_s} \, x_0 + \sqrt {1 - \bar {\alpha }_s} \cdot \varepsilon , \] where \( \bar {\alpha }_s = \prod _{j=1}^{s} \alpha _j \) is the cumulative signal retention up to step \( s \), and \( \varepsilon \sim \mathcal {N}(0, \mathbb {I}) \) is the latent noise variable that parameterizes the entire corruption trajectory.
At inference time, since we do not have access to \( x_0 \), we use the estimated denoised sample: \[ \hat {x}_0 = \frac {1}{\sqrt {\bar {\alpha }_t}} \left ( x_t - \sqrt {1 - \bar {\alpha }_t} \cdot \varepsilon _\theta (x_t, t) \right ), \] and reuse the predicted noise vector \( \varepsilon _\theta (x_t, t) \) to compute a deterministic transition to the earlier timestep \( x_s \): \[ x_s = \sqrt {\bar {\alpha }_s} \cdot \hat {x}_0 + \sqrt {1 - \bar {\alpha }_s} \cdot \varepsilon _\theta (x_t, t). \]
This formulation has several key benefits:
- It allows coarse timestep schedules without retraining — e.g., using 50 steps instead of 1000.
- The predicted noise \( \varepsilon _\theta (x_t, t) \) acts as a global direction, reused to guide the entire trajectory.
- The sampling process becomes non-Markovian — each step is computed from shared global information rather than local noise.
| DDPM: | \( x_T \to x_{T-1} \to x_{T-2} \to \dots \to x_1 \to x_0 \) | (1-step Gaussian update per transition) |
| DDIM: | \( x_T \to x_{t_1} \to x_{t_2} \to \dots \to x_1 \to x_0 \) | (larger steps, no sampling noise) |
Finally, note that directly jumping from \( x_T \) to \( \hat {x}_0 \) in one step is highly unstable: for large \( T \), the sample \( x_T \sim \mathcal {N}(0, \mathbb {I}) \) contains no useful structure. DDIM’s stepwise refinement — using intermediate predictions of \( \hat {x}_0 \) — enables better signal recovery through multiple corrections, while still avoiding the full 1000-step path of DDPM.
This construction motivates the next question: how is it valid to reuse the same noise vector across the entire trajectory? We now formalize that in the next part.
3. Why the “single–noise” picture is still correct The DDPM forward process injects fresh Gaussian noise at every step, defining a Markov chain \( q(x_t \mid x_{t-1}) \). This structure may suggest that different noise variables govern each transition. However, DDIM reveals that this is not necessary.
Key insight: forward marginals are closed-form. Despite the forward process being implemented as a chain of conditional Gaussians, its marginal at any timestep \( t \) is analytically tractable: \[ q(x_t \mid x_0) = \mathcal {N}\left ( \sqrt {\bar {\alpha }_t} \, x_0,\; (1 - \bar {\alpha }_t)\, \mathbb {I} \right ), \] which can be reparameterized as: \[ x_t = \sqrt {\bar {\alpha }_t} \, x_0 + \sqrt {1 - \bar {\alpha }_t} \cdot \varepsilon , \qquad \varepsilon \sim \mathcal {N}(0, \mathbb {I}). \] Thus, every sample \( x_t \) lies on a deterministic trajectory parameterized by a single global noise vector \( \varepsilon \), which DDIM aims to recover at test time.
DDPM training predicts this global noise. The model is trained using: \[ \mathcal {L}_{\mathrm {simple}} = \mathbb {E}_{x_0, t, \varepsilon } \left \| \varepsilon - \varepsilon _\theta (x_t, t) \right \|^2, \] meaning that the network learns to recover the same underlying \(\varepsilon \) that generated \( x_t \), regardless of the Markov structure used in implementation.
DDIM reuses this noise in reverse. Using the prediction \( \varepsilon _\theta (x_t, t) \), we estimate the clean image: \[ \hat {x}_0 = \frac {1}{\sqrt {\bar {\alpha }_t}} \left ( x_t - \sqrt {1 - \bar {\alpha }_t} \cdot \varepsilon _\theta (x_t, t) \right ), \] and reconstruct an earlier point \( x_s \) along the same trajectory as: \[ x_s = \sqrt {\bar {\alpha }_s} \cdot \hat {x}_0 + \sqrt {1 - \bar {\alpha }_s - \sigma _t^2} \cdot \varepsilon _\theta (x_t, t) + \sigma _t \cdot z, \quad z \sim \mathcal {N}(0, \mathbb {I}). \] In the deterministic case (\( \sigma _t = 0 \)), this constructs a smooth, invertible path backward. When \( \sigma _t > 0 \), stochasticity is added — not to resample new noise, but to reflect posterior uncertainty.
Why this reuse is consistent. At every new step \( x_s \), we pass the new pair \( (x_s, s) \) into the network and obtain a fresh prediction \( \varepsilon _\theta (x_s, s) \), which again approximates the same global noise vector \( \varepsilon \). Although DDIM reuses noise directionally from step to step, it still recomputes it from scratch at each stage — preserving consistency with the learned denoising function.
Conclusion:
- DDPM marginals are governed by a single noise vector \( \varepsilon \), not per-step randomness.
- DDPM training teaches the model to recover this latent vector from any \( x_t \).
- DDIM sampling reuses this direction — deterministically or stochastically — along a consistent generative trajectory.
- This makes DDIM both theoretically sound and fully compatible with DDPM training.
4. Optional Stochastic Extension DDIM supports a stochastic generalization of its reverse process, allowing a smooth tradeoff between determinism and diversity. For any reverse step \( t \to s \) with \( s < t \), the update becomes:
\[ x_s = \underbrace { \sqrt {\bar {\alpha }_s} \cdot \hat {x}_0 }_{\mbox{projected clean signal}} + \underbrace { \sqrt {1 - \bar {\alpha }_s - \sigma _{t \to s}^2} \cdot \varepsilon _\theta (x_t, t) }_{\mbox{denoising direction}} + \underbrace { \sigma _{t \to s} \cdot z }_{\mbox{stochastic noise}}, \qquad z \sim \mathcal {N}(0, \mathbb {I}), \] where: \[ \hat {x}_0 = \frac {1}{\sqrt {\bar {\alpha }_t}} \left ( x_t - \sqrt {1 - \bar {\alpha }_t} \cdot \varepsilon _\theta (x_t, t) \right ). \]
Term-by-Term Intuition:
- Projected clean signal: The model’s estimate \( \hat {x}_0 \) is projected from step \( t \) back to step \( s \) using the forward process statistics \( \bar {\alpha }_s \).
- Denoising direction: The score estimate \( \varepsilon _\theta (x_t, t) \) points back toward \( x_t \); scaling it reintroduces the appropriate amount of noise compatible with the forward marginal at step \( s \).
- Stochastic noise: The final term injects fresh Gaussian noise of variance \( \sigma _{t \to s}^2 \). When \( \sigma _{t \to s} = 0 \), the process is fully deterministic. When \( \sigma _{t \to s}^2 = \tilde {\beta }_t \cdot \frac {1 - \bar {\alpha }_s}{1 - \bar {\alpha }_t} \), the update recovers the DDPM reverse step.
Why This Works:
- Flexible yet faithful reverse step: The reverse mean is defined using the learned score (via \( \hat {x}_0 \)), while the variance \( \sigma _{t \to s}^2 \) is a tunable hyperparameter. Every choice in the interval \[ \sigma _{t \to s}^2 \in [0,\, \tilde {\beta }_t \cdot \tfrac {1 - \bar {\alpha }_s}{1 - \bar {\alpha }_t}] \] yields a valid generative step with unchanged forward marginals and training objective. In practice, most works set \( s = t - 1 \), reducing the bound to \( \tilde {\beta }_t \).
- Preserved training semantics: The forward process and training objective are left unchanged: \[ q(x_t \mid x_0) = \mathcal {N}(\sqrt {\bar {\alpha }_t} x_0,\; (1 - \bar {\alpha }_t)\, \mathbb {I}), \] and the model is trained to predict the noise \( \varepsilon \sim \mathcal {N}(0, \mathbb {I}) \) that produced \( x_t \). At inference time, this same prediction is reused, regardless of the stochasticity level \( \sigma _{t \to s} \).
-
Unbiased noise injection: The stochastic term \( \mathbf {z} \sim \mathcal {N}(0, \mathbb {I}) \) is added after the model predicts the denoising direction \( \boldsymbol {\epsilon }_\theta (\mathbf {x}_t, t) \). This ensures that:
- The model prediction remains unchanged regardless of the noise realization.
- The expectation over samples is centered on the deterministic prediction.
Thus, the added noise does not degrade the learned signal path but simply introduces controlled variation. This behavior approximates the uncertainty inherent in the true posterior \( q(\mathbf {x}_s \mid \mathbf {x}_t, \mathbf {x}_0) \), even though \( \mathbf {x}_0 \) is not available at test time. As a result, DDIM allows stochasticity without biasing or corrupting the generation trajectory.
-
Robustness to training mismatch: The only approximation is that future steps are now fed states \( x_s \) that include artificial noise \( \sigma _{t \to s} z \), not produced via the original forward chain. Nevertheless:
- This noise is still Gaussian and isotropic, matching the training distribution.
- For moderate \( \sigma _{t \to s} \), the deviation is small. Empirically, DDIM sampling remains stable and yields accurate denoising, as shown in Table 2 of [580].
Practical Implications:
- Deterministic vs. stochastic sampling: DDIM enables a continuum of generative behaviors, controllable via the noise parameter \( \sigma _{t \to s} \). Setting \( \sigma _{t \to s} = 0 \) yields fully deterministic sampling trajectories, ideal for tasks such as image editing, latent space interpolation, and reproducible evaluation. In contrast, using \( \sigma _{t \to s} = \sqrt {1 - \bar {\alpha }_s} \) or \( \sigma _{t \to s} = \tilde {\beta }_t \) restores stochasticity, producing diverse samples comparable to those from DDPM.
- Model reuse without retraining: The added noise term \( \sigma _t \mathbf {z} \), where \( \mathbf {z} \sim \mathcal {N}(0, \mathbb {I}) \), is injected after the network has predicted the denoising direction. Since this perturbation does not affect model outputs during training, DDIM sampling remains fully compatible with DDPM-trained networks. It requires no architectural changes or retraining and can be applied as a post-hoc modification at inference time.
- Flexible speed–diversity trade-off: DDIM supports coarser inference schedules (e.g., 50 or 100 steps) compared to the original 1000-step DDPM, significantly accelerating generation. Smaller values of \( \sigma _t \) lead to crisp, high-fidelity samples, while larger values increase diversity. Since \( \sigma _t \) is selected at test time, this trade-off remains fully user-controlled.
5. Advantages of DDIM Sampling
- Deterministic inference: High-quality samples can be generated without randomness.
- Speedup: Fewer timesteps (e.g., 25, 50, or 100 instead of 1000) yield strong results.
- No retraining required: DDIM reuses DDPM-trained noise predictors.
- Trajectory consistency: Sampling follows the learned denoising direction.
- Tunable diversity: Optional variance allows DDPM-like diversity when needed.
The result is a more flexible sampling framework that enables both efficient and expressive image generation — a critical step toward scaling diffusion models in practice.
For further insights and ablations, we refer the reader to [580], which introduces DDIM and empirically benchmarks its improvements.
Enrichment 20.9.4: Guidance Techniques in Diffusion Models
Diffusion models offer a flexible generative framework, but in their basic formulation, sample generation proceeds unconditionally from Gaussian noise. In many real-world settings, we want to steer this generation process — for example, to condition on class labels, textual prompts, or other forms of side information. This general strategy is known as guidance.
Guidance techniques modify the reverse diffusion process to bias samples toward desired outcomes while retaining high sample quality. These approaches do not alter the forward noising process, and instead inject additional directional information into the sampling dynamics — often by adjusting the reverse transition rule.
We now explore several influential guidance strategies, beginning with the original classifier guidance method introduced by Dhariwal and Nichol [122].
Classifier Guidance
The first major form of guidance was introduced by Dhariwal and Nichol [122] under the name classifier guidance. It extends DDPMs to class-conditional generation by injecting semantic feedback from a pretrained classifier into the sampling dynamics of the reverse diffusion process.
During training, the denoising network \( \epsilon _\theta (x_t, t) \) is trained as usual to predict the noise added at each timestep, following the standard DDPM objective. Separately, a classifier \( p_\phi (y \mid x_t) \) is trained to predict labels from noisy images \( x_t \) at various timesteps \( t \in [0, T] \). This is achieved by minimizing a standard cross-entropy loss over samples from the noising process. The classifier is trained after or in parallel with the diffusion model, and remains fixed during guided generation.
At inference time, we generate a trajectory by progressively denoising \( x_T \sim \mathcal {N}(0, I) \) toward \( x_0 \), using the reverse Gaussian transitions modeled by the network. To bias generation toward a particular class \( y \), we modify the reverse step by incorporating the gradient of the log-probability \( \log p_\phi (y \mid x_t) \) with respect to the current sample \( x_t \). This yields a modified score function via Bayes’ rule: \[ \nabla _{x_t} \log p(x_t \mid y) = \nabla _{x_t} \log p(x_t) + \nabla _{x_t} \log p(y \mid x_t), \] where the first term is the score of the unconditional model, and the second term comes from the classifier. Since DDPMs already learn an approximation to \( \nabla _{x_t} \log p(x_t) \), we can guide sampling by simply adding the classifier gradient.
In score-based language, the noise prediction is adjusted as: \[ \hat {\epsilon }_{\mbox{guided}}(x_t, t) = \hat {\epsilon }_\theta (x_t, t) - s \cdot \Sigma _t \nabla _{x_t} \log p_\phi (y \mid x_t), \] where:
- \( \hat {\epsilon }_\theta (x_t, t) \) is the denoiser’s prediction of the added noise,
- \( \Sigma _t \) is the variance of the reverse diffusion step at time \( t \),
- \( s > 0 \) is a tunable guidance scale that controls how strongly the generation is biased toward class \( y \).
In practice, the classifier gradient \( \nabla _{x_t} \log p_\phi (y \mid x_t) \) is computed by backpropagating through the logits of a pretrained classifier \( p_\phi (y \mid x_t) \), using automatic differentiation.
During sampling, this is done as follows:
- 1.
- Given the current noisy sample \( x_t \) and the desired class \( y \), compute the classifier’s logit vector \( \ell = f_\phi (x_t) \in \mathbb {R}^C \), where \( C \) is the number of classes.
- 2.
- Extract the log-probability of the target class: \( \log p_\phi (y \mid x_t) = \log \mathrm {softmax}(\ell )_y \).
- 3.
- Backpropagate this scalar with respect to the input \( x_t \) (not with respect to the model weights) to obtain the gradient: \[ \nabla _{x_t} \log p_\phi (y \mid x_t). \]
- 4.
- Add this gradient to the score function, scaled by the guidance factor \( s \), to steer the reverse update toward class \( y \).
At first glance, it may seem problematic to alter the denoising trajectory learned by the model. After all, the diffusion model is trained to predict noise that reverses the corruption process from \( x_{t} \) to \( x_{t-1} \), and adding arbitrary gradients could in principle interfere with that process.
However, the addition of the classifier gradient is not arbitrary—it is theoretically grounded. We remind that the reverse diffusion process samples from the conditional distribution \( p(x_t \mid y) \), and its associated score function is: \[ \nabla _{x_t} \log p(x_t \mid y) = \nabla _{x_t} \log p(x_t) + \nabla _{x_t} \log p(y \mid x_t), \] by Bayes’ rule. The unconditional model learns to approximate \( \nabla _{x_t} \log p(x_t) \) through score estimation or noise prediction. Adding \( \nabla _{x_t} \log p(y \mid x_t) \), which comes from the classifier, completes the full class-conditional score.
Thus, the classifier gradient is not changing the direction arbitrarily—it is restoring a missing piece of the full score function required for class-conditional generation. The classifier acts like a plug-in module that injects semantic preference into the learned dynamics, gently pulling the sample trajectory toward regions where \( x_t \) is likely to belong to class \( y \), without disrupting the overall denoising process.
Empirically, this simple mechanism has been shown to substantially improve both perceptual quality and class accuracy, particularly at moderate-to-high guidance scales \( s \in [1, 15] \). It steers trajectories toward semantically meaningful modes in the conditional distribution, leading to clearer, sharper outputs—often at the cost of some diversity, which can be tuned via the scale \( s \).
This mechanism makes classifier guidance a plug-and-play enhancement: any differentiable classifier can be used, and the guidance strength \( s \) can be tuned at inference time to balance fidelity and diversity.
Although classifier guidance is simple to implement and produces significantly sharper and more class-consistent samples, it does come with two practical drawbacks: it requires training and storing a separate classifier over noisy images, and it introduces extra computation at sampling time due to gradient evaluations at every timestep. These limitations motivate the development of classifier-free guidance, which we discuss next.
Classifier-Free Guidance
While classifier guidance enables powerful class-conditional generation, it comes with practical drawbacks: it requires training and storing a separate classifier, and incurs additional gradient computations at each sampling step. To overcome these limitations, Ho and Salimans [224] proposed a remarkably simple alternative: classifier-free guidance.
The key idea is to let the denoising model itself learn both the unconditional and class-conditional scores. That is, instead of training a separate classifier to inject \( \nabla _{x_t} \log p(y \mid x_t) \), we extend the model input to optionally accept conditioning information and teach it to interpolate between both behaviors.
Training Procedure Let \( \epsilon _\theta (x_t, t, y) \) denote a noise prediction model that is explicitly conditioned on a class label \( y \). The classifier-free guidance technique trains this model to operate in both conditional and unconditional modes using a simple dropout strategy on the conditioning signal.
Concretely, during training we sample a data-label pair \( (x_0, y) \sim q(x, y) \), and select a timestep \( t \in \{1, \dots , T\} \). We generate a noisy input \( x_t = \sqrt {\bar {\alpha }_t} x_0 + \sqrt {1 - \bar {\alpha }_t} \epsilon \) where \( \epsilon \sim \mathcal {N}(0, I) \), and then choose a conditioning label as: \[ \tilde {y} = \begin {cases} y & \mbox{with probability } 1 - p_{\mbox{drop}}, \\ \varnothing & \mbox{with probability } p_{\mbox{drop}}, \end {cases} \] where \( \varnothing \) denotes an empty or null token indicating that no label is provided.
We then minimize the standard DDPM loss: \[ \mathbb {E}_{x_0, t, \epsilon , y} \left [ \left \| \epsilon _\theta (x_t, t, \tilde {y}) - \epsilon \right \|^2 \right ], \] thus training the model to perform both conditional and unconditional denoising, depending on whether \( \tilde {y} \) is real or masked. In practice, \( p_{\mbox{drop}} \in [0.1, 0.5] \) provides a good trade-off between learning both behaviors.
How the Conditioning \( y \) is Incorporated. The conditioning variable \( y \) must be integrated into the denoising model in a way that allows the network to modulate its predictions based on class information (or other forms of conditioning such as text). The implementation depends on the nature of \( y \):
- For discrete class labels (e.g., in class-conditional image generation), \( y \in \{1, \dots , C\} \) is typically passed through a learnable embedding layer: \[ e_y = \mbox{Embed}(y) \in \mathbb {R}^d. \] This embedding is then added to or concatenated with the timestep embedding \( e_t = \mbox{Embed}(t) \) and used to modulate the network. A common design is to inject \( e_y \) into residual blocks via adaptive normalization (e.g., conditional BatchNorm or FiLM [479]) or as additive biases.
- For richer conditioning (e.g., language prompts or segmentation masks), \( y \) may be a sequence or tensor. In such cases, the network architecture includes a cross-attention mechanism to allow the model to attend to the context: \[ \mbox{CrossAttn}(q, k, v) = \mbox{softmax}\left ( \frac {q k^\top }{\sqrt {d}} \right ) v, \] where the keys \( k \) and values \( v \) come from an encoder applied to the conditioning input \( y \), and the queries \( q \) are derived from the image representation.
These mechanisms allow the model to seamlessly switch between conditional and unconditional modes by simply masking or zeroing out the embedding of \( y \) during classifier-free training.
Sampling with Classifier-Free Guidance At inference time, we leverage the model’s ability to perform both conditional and unconditional denoising. Given a noisy input \( x_t \) at timestep \( t \), we evaluate the model under two scenarios:
\begin {align*} \epsilon _{\text {cond}} &= \epsilon _\theta (x_t, t, y), \\ \epsilon _{\text {uncond}} &= \epsilon _\theta (x_t, t, \varnothing ), \end {align*}
where \( y \) is the conditioning label (e.g., a class or prompt), and \( \varnothing \) denotes an unconditional (empty) input. These predictions are combined using the interpolation formula:
\[ \epsilon _{\mbox{guided}} = \epsilon _{\mbox{uncond}} + s \cdot \left ( \epsilon _{\mbox{cond}} - \epsilon _{\mbox{uncond}} \right ), \]
where \( s \geq 1 \) is the guidance scale controlling the strength of conditioning. This can also be written as:
\[ \epsilon _{\mbox{guided}} = (1 + s) \cdot \epsilon _{\mbox{cond}} - s \cdot \epsilon _{\mbox{uncond}}. \]
The following piece of code illustrates how class labels are embedded and applied inside a diffusion architecture (e.g., U-Net):
import torch
from tqdm import tqdm
# Assumes the following are pre-initialized:
# - model: diffusion model (e.g., U-Net)
# - text_encoder: a frozen CLIP/T5-style encoder
# - tokenizer: matching tokenizer
# - scheduler: DDPM or DDIM scheduler with .step()
# - guidance_scale: e.g., 7.5
# - H, W: image dimensions (e.g., 64x64)
# Step 1: Define prompt(s)
prompts = ["a photo of a dog"] # List of text prompts
batch_size = len(prompts)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Step 2: Tokenize conditional and unconditional prompts
cond_tokens = tokenizer(prompts, padding=True, return_tensors="pt")
uncond_tokens = tokenizer([""] * batch_size, padding=True, return_tensors="pt")
# Step 3: Encode prompts into embeddings
text_cond = text_encoder(
input_ids=cond_tokens.input_ids.to(device),
attention_mask=cond_tokens.attention_mask.to(device)
).last_hidden_state # Shape: (B, T, D)
text_uncond = text_encoder(
input_ids=uncond_tokens.input_ids.to(device),
attention_mask=uncond_tokens.attention_mask.to(device)
).last_hidden_state # Shape: (B, T, D)
# Step 4: Concatenate for a single forward pass
text_embeddings = torch.cat([text_uncond, text_cond], dim=0) # Shape: (2B, T, D)
# Step 5: Initialize Gaussian noise
x = torch.randn((2 * batch_size, model.in_channels, H, W), device=device)
# Step 6: Reverse sampling loop
for t in tqdm(scheduler.timesteps):
t_batch = torch.full((2 * batch_size,), t, device=device, dtype=torch.long)
with torch.no_grad():
noise_pred = model(x, t_batch, encoder_hidden_states=text_embeddings).sample
noise_uncond, noise_cond = noise_pred.chunk(2) # Split into (B, ...) chunks
# Apply classifier-free guidance
guided_noise = noise_uncond + guidance_scale * (noise_cond - noise_uncond)
# Step the scheduler using only guided samples
x = scheduler.step(guided_noise, t, x[:batch_size]).prev_sample # Shape: (B, C, H, W)This simple pattern is powerful and generalizes across different modalities. In more complex systems such as Stable Diffusion [531], the conditional input \( y \) is often a text prompt embedded using a frozen transformer like CLIP [498], and passed through multiple layers of cross-attention throughout the U-Net decoder.
Why Classifier-Free Guidance Works: A Score-Based and Intuitive View Classifier-Free Guidance (CFG) builds on a simple yet powerful idea: train a single diffusion model to support both unconditional and conditional denoising behaviors. By exposing the model to both kinds of inputs during training, it becomes possible to steer generation toward a semantic target \( y \) without relying on a separate classifier.
To understand this, consider the decomposition of the conditional log-probability using Bayes’ rule: \begin {equation} \log p(x_t \mid y) = \log p(x_t) + \log p(y \mid x_t). \end {equation} Taking the gradient with respect to \( x_t \) yields: \begin {equation} \nabla _{x_t} \log p(x_t \mid y) = \nabla _{x_t} \log p(x_t) + \nabla _{x_t} \log p(y \mid x_t). \end {equation}
This tells us that the conditional score consists of two components:
- an unconditional score \( \nabla _{x_t} \log p(x_t) \), which represents the direction that increases likelihood under the overall data distribution;
- a label-specific influence \( \nabla _{x_t} \log p(y \mid x_t) \), which corrects the direction based on the conditioning variable \( y \).
In classifier guidance, the second term is approximated by a trained classifier. In classifier-free guidance, however, both terms are learned by the same model through a clever training trick: randomly dropping the conditioning label \( y \) (e.g., with 10% probability) and training the model to denoise in both settings.
Specifically:
- When \( y = \texttt{"dog"} \), the model sees noisy dog images \( x_t \) and learns to denoise them toward clean images \( x_0 \), guided by the label.
- When \( y \) is dropped, the model learns unconditional denoising: predicting \( x_0 \) without any external label.
As a result, the model implicitly learns: \begin {align} s_\theta (x_t, y, t) &\approx \nabla _{x_t} \log p(x_t \mid y), \quad \text {(conditional score)} \\ s_\theta (x_t, \varnothing , t) &\approx \nabla _{x_t} \log p(x_t), \quad \text {(unconditional score)} \end {align}
Subtracting these gives an approximation of the label’s effect: \begin {equation} s_\theta (x_t, y, t) - s_\theta (x_t, \varnothing , t) \approx \nabla _{x_t} \log p(y \mid x_t). \end {equation}
Intuition: This subtraction isolates the direction in feature space that pushes a sample toward better alignment with label \( y \). It’s as if we are extracting the “semantic vector field” attributable to the label alone. By multiplying this vector by a scale factor \( s \), we can amplify movement in the direction of the conditioning label.
Substituting into Bayes’ decomposition gives: \begin {equation} \nabla _{x_t} \log p(x_t \mid y) \approx s_\theta (x_t, \varnothing , t) + s \cdot \left ( s_\theta (x_t, y, t) - s_\theta (x_t, \varnothing , t) \right ), \end {equation} where \( s \in \mathbb {R}_{\geq 0} \) is a user-defined guidance scale.
In practice, most diffusion models are trained to predict noise \( \epsilon \) rather than the score directly. This reasoning therefore translates into the widely-used noise prediction rule: \begin {equation} \epsilon _{\mbox{guided}} = \epsilon _{\mbox{uncond}} + s \cdot \left ( \epsilon _{\mbox{cond}} - \epsilon _{\mbox{uncond}} \right ), \end {equation} where \( \epsilon _{\mbox{cond}} = \epsilon _\theta (x_t, t, y) \) and \( \epsilon _{\mbox{uncond}} = \epsilon _\theta (x_t, t, \varnothing ) \).
Conclusion. By training the model on noisy samples paired with and without the label, it learns how the presence of \( y \) modifies the denoising direction. At inference time, we explicitly compute and amplify this direction by subtracting the unconditional prediction and scaling the result. This lets us generate samples that are more aligned with the target concept, while preserving the stability of the underlying diffusion process.
Interpretation The difference \( \epsilon _{\mbox{cond}} - \epsilon _{\mbox{uncond}} \) approximates the semantic shift introduced by conditioning on \( y \). Scaling this difference by \( s \) amplifies the class- or prompt-specific features in the output, steering the model’s trajectory toward the desired mode. Larger values of \( s \) increase class adherence but may reduce diversity, reflecting a precision-recall trade-off in generation.
Typical Settings Empirically, guidance scales \( s \in [7.5, 10] \) often strike a good balance between fidelity and variation. Values \( s > 10 \) can produce oversaturated or collapsed samples, while \( s = 0 \) corresponds to pure unconditional generation.
Advantages Classifier-free guidance has become a cornerstone of modern diffusion-based systems because:
- It requires no auxiliary classifier: Conditioning is integrated directly into the denoiser, making the architecture self-contained.
- It avoids expensive gradient computations: No backward pass is needed during sampling.
- It enables dynamic guidance strength: Users can modulate \( s \) at test time without retraining the model.
- It generalizes beyond classes: The same technique applies to text prompts, segmentation maps, audio inputs, or any other conditioning.
Adoption in Large-Scale Models Classifier-free guidance is now standard in most large-scale diffusion pipelines, including:
- Imagen [540], which uses language conditioning on top of a super-resolution cascade,
- Stable Diffusion [531], where text embeddings from CLIP guide an autoencoding UNet,
- DALLE-2 [508], which uses CFG to synthesize and refine images from textual prompts.
This generality makes it one of the most practical and powerful tools for guided generative modeling with diffusion models.
Enrichment 20.9.5: Cascaded Diffusion Models
Motivation and Overview Diffusion models have achieved state-of-the-art results in image synthesis, but generating high-resolution samples directly (e.g., \(256 \times 256\) or larger) poses serious challenges. Large images require significantly more memory and computational resources, and a single generative model must capture both global structure and fine-grained detail. Additionally, standard denoising processes often struggle to coordinate long-range dependencies at such scales.
Cascaded Diffusion Models (CDMs), introduced by Ho et al. [225], address this issue by breaking the generation task into multiple stages. Instead of training a single large diffusion model for full-resolution synthesis, CDMs train a sequence of models:
- 1.
- A low-resolution base model generates a small image (e.g., \(64 \times 64\)) from Gaussian noise, conditioned on a class label \( y \).
- 2.
- One or more super-resolution models then refine this image, increasing resolution step-by-step (e.g., \(64 \to 128 \to 256\)) while maintaining semantic consistency and adding detail. Each model conditions on both the noisy image \( x_t \) and a low-resolution context image obtained by upsampling the previous model’s output.
This decomposition solves several problems:
- Scalability. Each model only needs to process a manageable resolution.
- Efficiency. Super-resolution models reuse coarse structure, focusing computation on adding detail.
- Modularity. Models can be trained and evaluated independently.
In the following parts, we describe the architectural design (U-Net-based blocks with multi-scale fusion), the training pipeline for both base and super-resolution models, and evaluation strategies for high-resolution cascaded generation.
Architecture: U-Net Design for Cascaded Diffusion Models Each component in the CDM pipeline—whether base generator or super-resolution model—uses a U-Net architecture tailored to its resolution level. This backbone supports spatial fidelity via multi-scale representations and skip connections.
Inputs and Their Roles in CDM Super-Resolution Models
Each super-resolution stage in a Cascaded Diffusion Model (CDM) functions as a conditional denoiser. Unlike naive super-resolution, which might learn a direct mapping from low-res to high-res, CDM stages begin from noise and learn to sample a distribution over plausible refinements, guided by a coarser input.
- Noisy high-resolution image \( x_t \): This is a sample from the standard forward diffusion process: \[ x_t = \sqrt {\bar {\alpha }_t} \, x_0 + \sqrt {1 - \bar {\alpha }_t} \, \epsilon , \qquad \epsilon \sim \mathcal {N}(0, I). \] Here, \( x_0 \) is a clean high-resolution image from the dataset, and \( t \in [0, 1] \) is a timestep. The model is trained to denoise \( x_t \) using information from the timestep \( t \), the class label \( y \), and a coarse guidance image \( z \). This preserves the probabilistic nature of generation: the network learns to sample detailed content rather than deterministically sharpen \( z \).
-
Low-resolution guide \( z \): This is a fixed, non-noisy input that anchors the high-resolution output to a previously generated image. It is computed as:
- 1.
- Downsample \( x_0 \) to the previous stage’s resolution (e.g., from \( 128 \times 128 \) to \( 64 \times 64 \)),
- 2.
- Then upsample it back to the current resolution using a deterministic interpolation method (e.g., bilinear upsampling).
The purpose of this two-step operation is to strip out high-frequency detail while retaining global structure and composition. The result \( z \) looks like a smoothed, coarse sketch of the final target image \( x_0 \). During training, this allows the network to learn how to ”fill in” fine details that are consistent with the structure in \( z \). During inference, the same structure is provided by upsampling a generated image from the previous resolution stage.
- Timestep embedding \( t \): The scalar \( t \in [0, 1] \) controls the level of corruption in \( x_t \). It is encoded using sinusoidal positional encodings or a learned MLP, and its embedding is added to feature maps at every layer of the U-Net. This informs the network about ”how much noise” remains in the input, and thereby how much denoising should be performed. Without this conditioning, the network would be unable to correctly localize the sample along the reverse trajectory.
- Class label \( y \): In class-conditional setups, the label is embedded (e.g., via a learned embedding table or projection) and added to intermediate layers in the U-Net—often by adding it to the same intermediate representation as \( t \). This helps guide the generation toward the correct semantic category.
Why Are Both \( x_t \) and \( z \) Needed?
Super-resolution diffusion models are trained to sample diverse, high-resolution outputs consistent with a low-res guide. These two inputs serve complementary roles:
- \( x_t \) introduces stochasticity—the model learns a distribution over high-res reconstructions, not a fixed sharpening process. Sampling from noise also enables diversity in outputs.
- \( z \) provides structural anchoring—it ensures that sampled outputs respect the layout, pose, and semantic structure already determined at the previous stage.
While it may seem redundant to denoise \( x_0 \) (which is already high-res), recall that we are not simply reconstructing \( x_0 \) deterministically—we are learning to sample high-resolution images consistent with \( z \). This formulation ensures that each CDM stage acts like a generative model in its own right, capable of producing diverse samples even when guided.
Training Procedure:
Each super-resolution model is trained independently as follows:
- 1.
- Sample a clean image \( x_0 \in \mathbb {R}^{H \times W \times C} \) from the dataset at the target resolution (e.g., \( 128 \times 128 \)).
- 2.
- Downsample \( x_0 \) to a lower resolution (e.g., \( 64 \times 64 \)), then upsample back to \( 128 \times 128 \) using bilinear interpolation to form the guide \( z \).
- 3.
- Sample a timestep \( t \sim \mathcal {U}[0,1] \) and generate \( x_t \sim q(x_t \mid x_0) \).
- 4.
- Train the model to predict \( \epsilon \) using a DDPM-style loss: \[ \mathbb {E}_{x_0, t, \epsilon , z, y} \left [ \| \epsilon _\theta (x_t, t, z, y) - \epsilon \|^2 \right ]. \]
Inference Pipeline:
Cascaded Diffusion Models (CDMs) generate high-resolution images by factorizing the generation process into a sequence of resolution-specific stages. Each stage operates at a different image resolution, beginning with a low-resolution semantic layout and progressively adding detail and refinement. Importantly, each stage follows its own denoising loop conditioned on the output of the previous stage.
- 1.
- Base generation stage (e.g., \( 64 \times 64 \)):
- Sample Gaussian noise: \( x_T^{(64)} \sim \mathcal {N}(0, I) \).
-
Apply a class-conditional diffusion model to denoise \( x_T^{(64)} \) over a sequence of reverse steps:
- For DDPM: iterate through all steps \( t = T, T{-}1, \dots , 1 \) using a stochastic update rule.
- For DDIM: select a subset of timesteps (e.g., 50) and apply a deterministic update rule with larger jumps in time.
- This produces a coarse but semantically correct image: \( \tilde {x}_0^{(64)} \sim p_{\mbox{model}}^{(64)}(x_0 \mid y) \).
- 2.
- Super-resolution stages (e.g., \( 128 \times 128 \), \( 256 \times 256 \)):
-
For each higher resolution:
- (a)
- Upsample: Resize \( \tilde {x}_0^{(\mbox{prev})} \) (e.g., bilinearly) to the current resolution to obtain the conditioning image \( z \).
- (b)
- Sample noise: Draw \( x_T^{(\mbox{target})} \sim \mathcal {N}(0, I) \) at the target resolution.
- (c)
- Denoise: Apply a class-conditional super-resolution diffusion model, conditioned on \( z \) and the class label \( y \), to iteratively denoise \( x_T^{(\mbox{target})} \) over its own timestep schedule (full or reduced), resulting in \( \tilde {x}_0^{(\mbox{target})} \).
-
Each stage performs a complete generation pass at its resolution: the base model synthesizes the semantic structure, and subsequent models enhance visual fidelity and fine details. Because the input noise \( x_T \) is sampled independently at each stage, and the conditioning image \( z \) is fixed throughout the reverse process, the pipeline is modular and supports parallel improvements at each resolution level.
Empirical Performance of CDMs Cascaded Diffusion Models (CDMs), proposed by Ho et al. [225], achieve strong performance in class-conditional image generation across multiple resolutions. On ImageNet at \( 64 \times 64 \), CDMs attain a Fréchet Inception Distance (FID) of 1.48 and an Inception Score (IS) of 67.95, outperforming prior baselines including BigGAN-deep (FID 4.06), Improved DDPM (FID 2.92), and ADM (FID 2.07). At higher resolutions, CDMs continue to excel: at \( 128 \times 128 \), they achieve an IS of 128.80 and FID of 3.52, while at \( 256 \times 256 \), they reduce FID to 4.88—beating Improved DDPM (FID 12.26), SR3 (FID 11.30), and ADM+upsampling (FID 7.49).
Beyond sample quality, CDMs demonstrate strong semantic alignment. At \( 128 \times 128 \), their generated samples achieve a Top-1 classification accuracy of 59.84% and Top-5 of 81.79%, substantially higher than BigGAN-deep (40.64% / 64.44%). At \( 256 \times 256 \), CDMs further narrow the gap to real data, achieving Top-1 / Top-5 scores of 63.02% / 84.06%, approaching the classification scores of real ImageNet samples (73.09% / 91.47%). These results underscore the effectiveness of CDMs as a scalable, modular pipeline for high-resolution image synthesis.
Enrichment 20.9.6: Progressive Distillation for Fast Sampling
Motivation Diffusion models have demonstrated exceptional generative capabilities, but suffer from a major limitation: slow sampling. Generating a single high-quality image typically requires hundreds to thousands of sequential steps, each invoking a deep neural network. This bottleneck arises from the structure of the reverse diffusion process — a Markov chain where each \( x_{t-1} \) depends on denoising \( x_t \), one step at a time.
A natural idea is to reduce sampling cost by skipping steps: instead of taking \( N \) fine-grained steps (e.g., 1000), why not just train a model to denoise using \( N/2 \), \( N/4 \), or even just a single step? The challenge lies in choosing how to perform these larger transitions. There are many possible denoising trajectories between \( x_T \sim \mathcal {N}(0,I) \) and a final sample \( x_0 \), and naively training a network to bridge them directly — without a clear path structure — often leads to poor results. The most common failure is blurry samples: the model learns to average over all plausible denoising paths, resulting in washed-out images that fail to capture sharp details or semantics.
This is where progressive distillation enters. Instead of learning an arbitrary large-step denoiser from scratch, we begin with a high-quality sampler — typically a DDIM — that already generates realistic images over many fine-grained steps. We then train a student model to imitate this specific sampling trajectory in fewer steps. Crucially, the student does not discover its own path; it learns to follow the teacher’s dynamics — a trajectory known to yield clean, sharp results.
Hence, instead of training from scratch, each student is supervised by a teacher that already performs high-quality generation. By repeating this process—e.g., distilling a 1000-step sampler into 500, then into 250, etc.—we amortize the cost of integration into fewer and fewer learned steps. Each round learns to approximate an already successful denoising schedule, which avoids mode averaging and retains the crispness of the teacher model’s outputs. This structured guidance is the key: we reduce sampling cost without sacrificing sample quality, achieving up to 2048\(\times \) speedups by compressing an 8192-step process into as few as 4 steps.
Pseudocode: Progressive Distillation Loop Inputs: Pretrained teacher model \( \hat {x}_\eta (z_t, t) \); dataset \( \mathcal {D} \); learning rate \( \gamma \); loss weighting function \( w(\lambda _t) \); initial number of sampling steps \( N \); cosine schedule \( \alpha _t = \cos (\tfrac {\pi }{2} t), \; \sigma _t = \sin (\tfrac {\pi }{2} t) \).
- 1.
- Initialize student model by copying the teacher: \( \hat {x}_\theta \leftarrow \hat {x}_\eta \)
- 2.
- Repeat until \( N = 4 \):
- (a)
- Halve the number of steps: \( N \gets N / 2 \)
- (b)
- Train the student:
- i.
- Sample data \( x_0 \sim \mathcal {D} \)
- ii.
- Sample index \( i \sim \mbox{Uniform}\{1, \dots , N\} \), compute \( t = i / N \)
- iii.
- Sample noise \( \epsilon \sim \mathcal {N}(0, I) \)
- iv.
- Generate noisy input: \[ z_t = \alpha _t x_0 + \sigma _t \epsilon \]
- v.
- Generate teacher trajectory (two DDIM steps):
- Step 1:
-
Let \( t' = t - 0.5/N \). Then: \[ z_{t'} = \alpha _{t'} \hat {x}_\eta (z_t, t) + \frac {\sigma _{t'}}{\sigma _t} \left ( z_t - \alpha _t \hat {x}_\eta (z_t, t) \right ) \]
- Step 2:
-
Let \( t'' = t - 1/N \). Then: \[ z_{t''} = \alpha _{t''} \hat {x}_\eta (z_{t'}, t') + \frac {\sigma _{t''}}{\sigma _{t'}} \left ( z_{t'} - \alpha _{t'} \hat {x}_\eta (z_{t'}, t') \right ) \]
- Inversion to get student target:
-
Solve for the denoised estimate that would produce \( z_{t''} \) in one coarse step from \( z_t \): \[ \tilde {x}_0 = \frac { z_{t''} - \left ( \frac {\sigma _{t''}}{\sigma _t} \right ) z_t }{ \alpha _{t''} - \left ( \frac {\sigma _{t''}}{\sigma _t} \right ) \alpha _t } \]
- vi.
- Train the student model:
- Log-SNR:
-
\[ \lambda _t = \log \left ( \frac {\alpha _t^2}{\sigma _t^2} \right ) \]
- Loss:
-
\[ \mathcal {L}_\theta = w(\lambda _t) \cdot \left \| \hat {x}_\theta (z_t, t) - \tilde {x}_0 \right \|^2 \]
- Gradient update:
-
\[ \theta \gets \theta - \gamma \nabla _\theta \mathcal {L}_\theta \]
- (c)
- Promote student to teacher: \( \hat {x}_\eta \gets \hat {x}_\theta \)
Prerequisites Required to Understand The Progressive Distillation Loop In diffusion models, the forward process gradually corrupts a clean input \(x_0\) by adding Gaussian noise across time steps. At diffusion step \(t \in \{1, \dots , T\}\), the noisy sample \(x_t\) is defined as:
\[ x_t = \sqrt {\bar {\alpha }_t} \cdot x_0 + \sqrt {1 - \bar {\alpha }_t} \cdot \epsilon , \quad \epsilon \sim \mathcal {N}(0, I), \]
where the parameters \(\bar {\alpha }_t\), \(\alpha _t\), and \(\sigma _t\) follow a predefined noise schedule. We now clarify their definitions and explain their role:
- Instantaneous noise factor: \( \alpha _t = \sqrt {1 - \beta _t}, \quad \mbox{with } \beta _t \in (0, 1) \mbox{ being the per-step noise variance.} \) This coefficient determines how much of the current sample \(x_{t-1}\) is retained during the forward transition \(x_{t-1} \rightarrow x_t\): \( x_t = \alpha _t x_{t-1} + \sqrt {1 - \alpha _t^2} \cdot \epsilon . \)
- Cumulative signal retention: \[ \bar {\alpha }_t = \prod _{s=1}^t \alpha _s^2. \] This is the total fraction of the original signal \( x_0 \) that survives up to step \( t \). It appears in the closed-form expression for direct sampling of \( x_t \) from \( x_0 \).
- Cumulative noise variance: \[ \sigma _t^2 = 1 - \bar {\alpha }_t, \qquad \sigma _t = \sqrt {1 - \bar {\alpha }_t}. \] These describe the total noise variance and standard deviation added by time \( t \). The form ensures that \( x_t \sim \mathcal {N}(0, I) \) when \( t = T \) and the original signal is fully destroyed.
Cosine Formulation and Angular Parameterization (Continuous-Time)
In continuous-time diffusion models—such as DDIM [580] and progressive distillation—the forward noising process is often rewritten using a unit-norm angular parameterization:
\[ z_t = \alpha _t x_0 + \sigma _t \epsilon , \qquad \mbox{where } \alpha _t^2 + \sigma _t^2 = 1, \quad \epsilon \sim \mathcal {N}(0, I). \]
This formulation treats \((\alpha _t, \sigma _t)\) as a point on the unit circle in 2D signal–noise space. The coefficients are defined via a cosine-based schedule [449]:
\[ \alpha _t = \cos \left ( \frac {\pi }{2} t \right ), \qquad \sigma _t = \sin \left ( \frac {\pi }{2} t \right ), \qquad t \in [0, 1]. \]
This setup has several important properties and motivations:
- Variance Preservation: The identity \(\alpha _t^2 + \sigma _t^2 = 1\) ensures that \(z_t \sim \mathcal {N}(0, I)\) for any \(t\) if \(x_0 \sim \mathcal {N}(0, I)\). This keeps the total energy constant throughout the forward process.
- Smooth Signal–Noise Transition: As \( t \to 0 \), we have \( \alpha _0 = 1 \), \( \sigma _0 = 0 \), so \( z_0 = x_0 \) (fully clean). As \( t \to 1 \), \( \alpha _1 = 0 \), \( \sigma _1 = 1 \), so \( z_1 = \epsilon \sim \mathcal {N}(0, I) \) (fully noisy). The cosine schedule smoothly interpolates between these extremes.
- Uniform Angular Spacing: The cosine function parameterizes a half-circle, so linear values of \( t \in [0, 1] \) correspond to evenly spaced angular positions \( \theta _t \in [0, \frac {\pi }{2}] \). This gives simple geometric control over the signal-to-noise tradeoff, which is particularly useful for reverse-time interpolation in distillation.
This angular schedule underlies the reparameterized sample construction and simplifies both training and inference in distillation frameworks. It also facilitates velocity-parameterized losses, cosine-SNR analysis, and efficient teacher-student approximation schemes—all of which are explored in subsequent sections.
What Is SNR and Why Use It? The signal-to-noise ratio (SNR) at time \( t \) quantifies how much of \( z_t \) comes from signal \( x_0 \) versus noise \( \epsilon \). Since both \( x_0 \) and \( \epsilon \) are standard Gaussian and independent, their variances scale as: \[ \mathrm {Var}[\alpha _t x_0] = \alpha _t^2, \qquad \mathrm {Var}[\sigma _t \epsilon ] = \sigma _t^2. \]
Thus, SNR is defined as: \[ \mathrm {SNR}(t) = \frac {\mathrm {Signal \ Variance}}{\mathrm {Noise \ Variance}} = \frac {\alpha _t^2}{\sigma _t^2}. \]
This ratio captures the amount of recoverable information at each timestep and naturally guides loss weighting: larger SNR implies more signal (thus lower error tolerance), while smaller SNR implies more noise.
Instead of using raw SNR, the training loss is often weighted by log-SNR: \[ \lambda _t = \log \left ( \frac {\alpha _t^2}{\sigma _t^2} \right ), \] which stabilizes training and improves numerical behavior over a wide range of \( t \).
Cosine Schedule and Angular Construction In progressive distillation, the pair \( (\alpha _t, \sigma _t) \) is chosen from an angular cosine schedule: \[ \alpha _t = \cos \left ( \frac {\pi }{2} t \right ), \qquad \sigma _t = \sin \left ( \frac {\pi }{2} t \right ), \] so that:
- \( \alpha _0 = 1 \), \( \sigma _0 = 0 \) at clean input,
- \( \alpha _1 = 0 \), \( \sigma _1 = 1 \) at full noise,
- \( \alpha _t^2 + \sigma _t^2 = 1 \) (variance-preserving).
The angle \( \phi _t = \arctan \left ( \frac {\sigma _t}{\alpha _t} \right ) \) linearly spans \( [0, \pi /2] \), enabling tractable interpolation over time and across sampled points \( t, t - \delta \), etc. This smooth interpolation is critical for trajectory matching during teacher-student distillation.
Teacher Trajectory Construction via Two DDIM Steps Progressive distillation [542] accelerates the denoising process by training a student model to mimic multiple steps of a teacher sampler in one. Specifically, the student learns to match the result of two consecutive DDIM steps taken by the teacher — compressing them into a single coarse jump. This requires constructing a deterministic trajectory using the teacher and inverting it to generate a suitable training target for the student.
DDIM Reverse Update Rule.
In DDIM [580], the denoising process is deterministic and parameterized by the model’s prediction of the clean sample \( \hat {x}_0 \). The reverse update from timestep \( t \to t' \) is given by: \[ z_{t'} = \alpha _{t'} \hat {x}_0 + \frac {\sigma _{t'}}{\sigma _t} (z_t - \alpha _t \hat {x}_0), \] where \( \alpha _t = \cos (\tfrac {\pi }{2}t) \), \( \sigma _t = \sin (\tfrac {\pi }{2}t) \), and \( z_t = \alpha _t x_0 + \sigma _t \epsilon \) is the noisy latent at normalized time \( t \in [0,1] \).
This formula arises from analytically rewriting the DDPM forward process and selecting a particular sampling path that preserves total variance. It provides a time-scaled interpolation between the current noisy sample \( z_t \) and the predicted denoised image \( \hat {x}_0 \), allowing a smooth deterministic trajectory from noise to signal.
Constructing the Two-Step Teacher Trajectory.
Let \( t \in [0, 1] \) be a coarse timestep from the student’s schedule, where \( N \) is the total number of denoising steps in the current distillation round. To simulate how the teacher would behave with finer resolution, we define two intermediate substeps: \[ t' = t - \frac {0.5}{N}, \qquad t'' = t - \frac {1}{N}. \] These are symmetrically spaced between \( t \) and the next coarse timestep in the student’s schedule. In other words, if the student will jump from \( t \to t'' \), then the teacher simulates two finer-grained hops \( t \to t' \to t'' \) that evenly divide the interval. This alignment ensures that the student’s coarse step has a faithful, high-resolution trajectory to imitate.
Step 1: From \( z_t \) to \( z_{t'} \).
We begin with a deterministic DDIM update, using the teacher’s prediction \( \hat {x}_\eta (z_t, t) \). This quantity corresponds to the predicted clean image \( \hat {x}_0 \) in the DDIM update rule: \[ z_{t'} = \alpha _{t'} \hat {x}_0 + \frac {\sigma _{t'}}{\sigma _t} (z_t - \alpha _t \hat {x}_0). \] Substituting \( \hat {x}_\eta (z_t, t) \) in place of \( \hat {x}_0 \), we compute: \[ z_{t'} = \alpha _{t'} \hat {x}_\eta (z_t, t) + \frac {\sigma _{t'}}{\sigma _t} \left ( z_t - \alpha _t \hat {x}_\eta (z_t, t) \right ). \]
Step 2: From \( z_{t'} \) to \( z_{t''} \).
After reaching \( z_{t'} \), the teacher performs a second deterministic DDIM step, using a fresh denoised prediction at the new timepoint. Specifically, it computes \( \hat {x}_\eta (z_{t'}, t') \), which—just like before—plays the role of \( \hat {x}_0 \) in the standard DDIM formulation. The update becomes: \[ z_{t''} = \alpha _{t''} \hat {x}_\eta (z_{t'}, t') + \frac {\sigma _{t''}}{\sigma _{t'}} \left ( z_{t'} - \alpha _{t'} \hat {x}_\eta (z_{t'}, t') \right ). \]
This completes the teacher’s fine-grained trajectory from \( z_t \to z_{t'} \to z_{t''} \), constructed entirely from deterministic DDIM steps. It is important to emphasize that although both \( \hat {x}_\eta (z_t, t) \) and \( \hat {x}_\eta (z_{t'}, t') \) are predictions of the clean image, each corresponds to a different timepoint and is used independently in its respective update. No change to the DDIM formula is required—the teacher simply follows two consecutive applications of the same rule.
Inverting the Trajectory: Computing the Student’s Target \( \tilde {x}_0 \)
To mimic the teacher’s fine-grained two-step path \( z_t \to z_{t'} \to z_{t''} \) using only a single coarse step, the student must predict a clean image \( \tilde {x}_0 \) such that its own DDIM update lands exactly at \( z_{t''} \). Assuming the student uses the same deterministic DDIM update rule, we require: \[ z_{t''} = \alpha _{t''} \tilde {x}_0 + \frac {\sigma _{t''}}{\sigma _t} (z_t - \alpha _t \tilde {x}_0). \] Solving for \( \tilde {x}_0 \) gives a closed-form expression: \[ \tilde {x}_0 = \frac {z_{t''} - \left ( \tfrac {\sigma _{t''}}{\sigma _t} \right ) z_t}{\alpha _{t''} - \left ( \tfrac {\sigma _{t''}}{\sigma _t} \right ) \alpha _t}. \]
What \( \hat {x}_0 \) and \( \tilde {x}_0 \) represent
- \( \hat {x}_0 \): A predicted denoised image produced by either the teacher or student at a given timepoint — e.g., \( \hat {x}_\eta (z_t, t) \) — used to advance the DDIM trajectory.
- \( \tilde {x}_0 \): An artificial target constructed via DDIM inversion, guiding the student to match the full two-step path of the teacher using a single update.
How this resolves DDPM’s low-SNR limitations
In standard DDPM training [223], the model is trained to predict the additive noise \( \epsilon \) via: \[ \mathcal {L}_{\mbox{DDPM}} = \left \| \epsilon - \epsilon _\theta (z_t, t) \right \|^2, \] which is equivalent to denoising supervision when rewritten as: \[ \left \| x_0 - \hat {x}_\theta (z_t, t) \right \|^2 \cdot \frac {\alpha _t^2}{\sigma _t^2} = w(\lambda _t) \cdot \left \| x_0 - \hat {x}_\theta (z_t, t) \right \|^2, \] with \[ \lambda _t = \log \left ( \frac {\alpha _t^2}{\sigma _t^2} \right ), \quad w(\lambda _t) = \exp (\lambda _t). \]
This weighting scheme is effective for long diffusion schedules where denoising starts in moderate-to-high SNR regions. But in progressive distillation — where the student starts from high \( t \) values and the number of steps is drastically reduced (e.g., 1000 \( \to \) 4) — the student must denoise from latents \( z_t \sim \mathcal {N}(0, I) \) with virtually no remaining signal. That is: \[ \mbox{SNR}(t) = \frac {\alpha _t^2}{\sigma _t^2} \ll 1 \quad \mbox{as } t \to 1. \]
Failure Modes at Low SNR
This low-SNR regime is not inherently problematic in standard DDPM/DDIM settings, where sampling begins from noise but proceeds through many finely spaced steps. Each reverse update makes a small correction, gradually increasing signal and enabling stable recovery of \( x_0 \).
However, in progressive distillation, the sampling path is aggressively compressed. The student is expected to perform large denoising jumps — often starting from high values of \( t \) where \( z_t \sim \mathcal {N}(0, I) \), but reaching nearly clean states in just a few steps. Without the benefit of a gradual signal buildup, this one-step transition from low to high SNR introduces two key failure modes:
- 1.
- Exploding Gradients: In noise-prediction formulations, the model outputs an estimate \( \epsilon _\theta (z_t, t) \), which is later transformed into a clean reconstruction via: \[ \hat {x}_0 = \frac {z_t - \sigma _t \cdot \epsilon _\theta (z_t)}{\alpha _t}. \] However, when \( \alpha _t \ll 1 \), this division magnifies even small prediction errors in \( \epsilon _\theta \), leading to unstable gradients during training. This effect worsens at large \( t \), where the latent \( z_t \) is dominated by noise and provides limited information about the underlying signal.
- 2.
- Vanishing Supervision: Standard DDPM training implicitly scales the regression loss in image space by the log-SNR-based factor: \[ w(\lambda _t) = \exp (\lambda _t) = \frac {\alpha _t^2}{\sigma _t^2}. \] As \( \lambda _t \to -\infty \) (i.e., \( \alpha _t^2 \to 0 \)), this weight shrinks to zero, diminishing the contribution of early, noisy timesteps to the overall training objective. Yet these are precisely the timesteps where strong supervision is most crucial, since the model must perform large, uncertain denoising transitions.
How Progressive Distillation Addresses These Issues
- Numerically Stable DDIM Inversion Target \( \tilde {x}_0 \): Rather than recovering \( x_0 \) from predicted noise — which involves division by small \( \alpha _t \) — progressive distillation sidesteps the instability by directly supervising the student with an analytically computed target: \[ \tilde {x}_0 = \frac {z_{t''} - \left ( \frac {\sigma _{t''}}{\sigma _t} \right ) z_t}{\alpha _{t''} - \left ( \frac {\sigma _{t''}}{\sigma _t} \right ) \alpha _t}, \] where \( z_{t''} \) is obtained from the teacher’s deterministic two-step DDIM trajectory. This inversion expresses \( \tilde {x}_0 \) purely in terms of known latents and schedule parameters, ensuring that it remains well-scaled even when \( \alpha _t \to 0 \). Crucially, this avoids reliance on unstable backward conversions of predicted noise into signal.
-
Loss Weighting That Remains Active at Low SNR: To preserve supervision across all timesteps — including those where the signal is weak — progressive distillation replaces the conventional SNR-based weight \( w(\lambda _t) = \exp (\lambda _t) \) with more robust alternatives:
- Truncated Log-SNR Weighting: \[ w(t) = \max \left ( \log \left ( \frac {\alpha _t^2}{\sigma _t^2} \right ), \lambda _{\min } \right ), \] where \( \lambda _{\min } \) is a tunable floor that prevents the weight from collapsing to negative infinity. This ensures that gradients remain non-negligible even in the most noise-dominated steps.
- SNR+1 Weighting: \[ w(t) = \frac {\alpha _t^2}{\alpha _t^2 + \sigma _t^2}, \] which is bounded between 0 and 1 and smoothly transitions as a function of time. Unlike exponential decay, this formulation retains meaningful weight even at low SNR, while still emphasizing timesteps with stronger signal.
Both weighting strategies are designed to prevent early training steps from being overwhelmed by numerical instability or under-emphasized due to vanishing loss terms — two common failure points in highly compressed denoising schedules.
Conclusion
Progressive distillation introduces unique challenges due to its compressed sampling schedule, where the model must denoise aggressively from extremely noisy latents in just a few steps. To address the resulting low-SNR difficulties, the training procedure incorporates two key modifications:
- It mitigates exploding reconstruction errors by replacing unstable noise-to-image inversions with a direct and well-conditioned target \( \tilde {x}_0 \), avoiding any division by \( \alpha _t \).
- It avoids supervision collapse by modifying the loss weighting scheme to remain active even when \( \mbox{SNR}(t) \approx 0 \), ensuring meaningful gradients in the earliest and noisiest student steps.
These innovations make it possible to train compact student samplers that achieve high-fidelity generation in as few as 2–4 steps — a remarkable improvement in diffusion model efficiency.
Empirical Results and Sample Quality The effectiveness of progressive distillation is best understood through its impact on both sample quality and inference efficiency. The following figure compares the Fréchet Inception Distance (FID) scores achieved by distilled samplers on several datasets and resolution settings, evaluated at various sampling step budgets.
Key observations:
- On all datasets, the distilled model converges to comparable or better FID than DDIM with only a fraction of the steps.
- In unconditional CIFAR-10, the distilled sampler with just \( 4 \) steps achieves FID ˜2.1 — competitive with 50–100 step DDIM samplers.
These results validate the intuition behind distillation: rather than relying on numerical integration of the reverse-time SDE or ODE, we amortize this trajectory into a fixed sampler that mimics the high-quality path. As a result, inference can proceed in as few as 4–8 steps — reducing cost by more than an order of magnitude without noticeable degradation in fidelity.
Stochastic vs. Deterministic Baselines. The experiments also include a tuned stochastic sampler, where variance schedules are optimized via log-scale interpolation between upper and lower bounds (following Nichol & Dhariwal, 2021). For each number of steps, the interpolation coefficient is manually tuned to yield the best results. Still, progressive distillation matches or outperforms these handcrafted alternatives — showing that learning to mimic a deterministic high-quality sampler is more effective than manually adjusting variance schedules.
Conclusion Progressive distillation transforms diffusion models from slow, high-fidelity samplers into efficient generative tools by compressing the sampling process into a small number of learned denoising steps. Rather than predicting noise in an unstable low-SNR regime, each distilled model learns to reproduce the behavior of a high-quality sampler using a fraction of the original steps. This amortized integration not only accelerates generation by orders of magnitude but does so without sacrificing sample quality — as evidenced across diverse datasets and resolutions. As a result, progressive distillation provides a principled, scalable solution to one of the most critical bottlenecks in diffusion-based generative modeling.
Enrichment 20.9.7: Velocity-Space Sampling: Learning Denoising Trajectories
After DDPMs introduced stochastic denoising and DDIMs offered a deterministic alternative by exploiting the latent-noise parameterization, a natural question arises: can we model the entire denoising trajectory more directly and efficiently? Velocity-space sampling (V-Space sampling) offers a compelling answer.
Instead of predicting the noise \( \boldsymbol {\varepsilon } \) added during forward diffusion (as in DDPM) or using it to reconstruct \( \mathbf {x}_0 \) (as in DDIM), velocity-space sampling proposes to predict a new quantity: the instantaneous velocity of the sample at time \( t \). Specifically, the model learns a vector field \( \mathbf {v}_\theta (\mathbf {x}_t, t) \in \mathbb {R}^d \) that describes how each point should evolve over time: \[ \frac {d}{dt} \mathbf {x}_t = \mathbf {v}_\theta (\mathbf {x}_t, t). \] This transforms sampling into a continuous-time trajectory defined by an ordinary differential equation (ODE), offering a geometric interpretation of the denoising process as movement along smooth, learned flow lines in image space.
In practice, the velocity target is derived from the known forward diffusion process. Given the reparameterized forward sampling: \[ \mathbf {x}_t = \sqrt {\bar {\alpha }_t} \, \mathbf {x}_0 + \sqrt {1 - \bar {\alpha }_t} \, \boldsymbol {\varepsilon }, \quad \boldsymbol {\varepsilon } \sim \mathcal {N}(\mathbf {0}, \mathbf {I}), \] the velocity target becomes: \[ \mathbf {v}_\theta (\mathbf {x}_t, t) = \frac { \sqrt {\bar {\alpha }_t} \, \boldsymbol {\varepsilon }_\theta (\mathbf {x}_t, t) - \sqrt {1 - \bar {\alpha }_t} \, \mathbf {x}_t } { \sqrt {\bar {\alpha }_t (1 - \bar {\alpha }_t)} }. \] This transformation is a linear combination of the predicted residual noise and the input \( \mathbf {x}_t \), producing smoother and more temporally stable dynamics than direct noise or image predictions.
During training, the model minimizes the mean squared error between the predicted velocity and the oracle velocity derived from the forward process: \[ \mathcal {L}_{\mbox{vel}}(\theta ) = \mathbb {E}_{\mathbf {x}_0, \boldsymbol {\varepsilon }, t} \left [ \left \| \mathbf {v}_\theta (\mathbf {x}_t, t) - \mathbf {v}_{\mbox{oracle}}(\mathbf {x}_t, t) \right \|^2 \right ], \] where \( \mathbf {x}_t \) is computed from \( \mathbf {x}_0 \) and \( \boldsymbol {\varepsilon } \) as above. This loss replaces the conventional noise-prediction loss used in DDPMs.
Velocity-based sampling offers several practical and conceptual advantages:
- Smoother dynamics: Velocities vary more smoothly across time than raw noise or image values, resulting in a more stable back-propagation signal.
- Faster sampling: Models trained in velocity space can generate competitive samples in as few as 20–35 steps on complex datasets such as ImageNet.
- Compatibility: The network architecture remains unchanged from DDPM; only the training target shifts from noise to velocity.
- Interpretability: The model learns a continuous flow field, providing a geometric interpretation of how data points evolve toward the data manifold.
While velocity-space sampling offers a more structured and smoother alternative to raw noise prediction, it still inherits its supervision targets from the diffusion process. That is, the oracle velocity \( \mathbf {v}_{\mbox{oracle}} \) is implicitly defined by the reverse-time dynamics of a predefined forward SDE. As such, training remains dependent on a specific generative trajectory and inherits the inductive biases of the diffusion process used to define it.
Flow Matching generalizes this idea by decoupling the supervision of the velocity field from any fixed stochastic process. Instead of learning to imitate a reverse diffusion path, Flow Matching constructs explicit, analytically-defined velocity fields that transport a source distribution to a target distribution. This enables direct supervision of the vector field—bypassing both diffusion dynamics and likelihood estimation—and allows for greater flexibility in how generative trajectories are defined and optimized.
Enrichment 20.10: Flow Matching: Beating Diffusion Using Flows
Background and Motivation. Flow Matching is a principled approach to training continuous-time generative models. It belongs to the broader class of flow-based methods, which generate data by transforming samples from a simple source distribution \( p_0 \) (e.g., standard Gaussian) into a complex target distribution \( p_1 \) (e.g., natural images). Rather than applying a fixed sequence of discrete transformations, Flow Matching models this evolution as a continuous progression of probability densities over time, forming a smooth probability path \( (p_t)_{t \in [0,1]} \) with \( p_0 = p \) and \( p_1 = q \).
\[ \begin {array}{c} \mbox{Generative Models} \\ \rotatebox [origin=c]{90}{$\subset $} \\ \underbrace {\mbox{Flow Models}}_{\mbox{ODE-based transformations}} \\ \rotatebox [origin=c]{90}{$\subset $} \\ \underbrace {\textbf {Flow Matching}}_{\mbox{learns velocity fields directly}} \\ \rotatebox [origin=c]{90}{$\subset $} \\ \mbox{Diffusion Models (DDPM/DDIM)} \end {array} \]
To transform samples from a simple initial distribution \( p_0 \) into more complex samples from a target distribution \( p_1 \), we define a continuous path in sample space parameterized by time \( t \in [0,1] \). This transformation is governed by a deterministic ordinary differential equation (ODE) that describes how each point \( x_t \in \mathbb {R}^d \) should evolve over time.
At the heart of this dynamic system is a learnable velocity field \( v_t : \mathbb {R}^d \to \mathbb {R}^d \), which assigns to every point \( x \) a direction and magnitude of motion at each time \( t \). The evolution of a sample \( x_t \) under this field is given by the initial value problem: \[ \frac {d}{dt} x_t = v_t(x_t), \qquad x_0 \sim p_0. \] This differential equation describes a trajectory in space that the sample follows over time, beginning at an initial point \( x_0 \). Conceptually, we can think of the sample as a particle moving through a fluid whose flow is described by \( v_t \).
To formalize this idea, we define a time-dependent trajectory map \( \psi _t : \mathbb {R}^d \to \mathbb {R}^d \), where \( \psi _t(x_0) \) denotes the location of the particle at time \( t \) that started from position \( x_0 \) at time zero. By the chain rule, the rate of change of the map is governed by the velocity evaluated at the current position: \[ \frac {d}{dt} \psi _t(x_0) = v_t(\psi _t(x_0)), \qquad \psi _0(x_0) = x_0. \] This equation simply states that the motion of the transformed point \( \psi _t(x_0) \) is dictated by the velocity vector at its current location and time. It ensures that the path traced by \( \psi _t(x_0) \) is consistent with the flow defined by the velocity field.
Under mild regularity conditions—specifically, that \( v_t(x) \) is locally Lipschitz continuous in \( x \) and measurable in \( t \)—the Picard–Lindelöf theorem guarantees that the ODE has a unique solution for each initial point \( x_0 \) and for all \( t \in [0,1] \) [480]. This means the trajectory map \( \psi _t \) defines a unique and smooth deformation of space over time, continuously transporting samples from the initial distribution \( p_0 \) toward the desired target \( p_1 \).
Yet ensuring well-defined trajectories is not sufficient: we must also guarantee that the distribution of points evolves consistently. To this end, the time-varying density \( p_t \) must satisfy the continuity equation: \[ \frac {d}{dt} p_t(x) + \nabla \cdot \left (p_t(x) \, v_t(x)\right ) = 0. \]
This partial differential equation enforces conservation of probability mass. The term \( j_t(x) = p_t(x) v_t(x) \) represents the probability flux at point \( x \), and the divergence \( \nabla \cdot j_t(x) \) quantifies the net outflow. Thus, the continuity equation ensures that changes in density arise solely from mass flowing in or out under the velocity field.
A velocity field \( v_t \) is said to generate the probability path \( p_t \) if the pair \( (v_t, p_t) \) satisfies this equation at all times \( t \in [0,1) \). This guarantees that the sample trajectories \( x_t = \psi _t(x_0) \), drawn from \( x_0 \sim p_0 \), induce an evolving density \( p_t \) that converges to the desired target \( p_1 \). This coupling of geometry and distribution is what makes Flow Matching a distribution-consistent framework for generative modeling.
Why Flow Matching? Diffusion models such as DDPM and DDIM generate data by simulating a stochastic process in reverse—starting from Gaussian noise and iteratively denoising across hundreds or even thousands of discretized timesteps. Although highly effective, this sampling procedure is computationally expensive. Moreover, training such models involves approximating the score function \( \nabla _x \log p_t(x) \) or optimizing a variational objective (e.g., an ELBO), both of which rely on intricate reweighting schemes and carefully tuned noise schedules.
Flow Matching [364] offers a deterministic and simulation-free alternative. Rather than estimating a score or a generative likelihood, it directly learns a time-dependent velocity field \( v_t(x) \) that transports mass along a prescribed probability path \( (p_t)_{t \in [0,1]} \). Once trained, the model generates new samples by solving a single ODE: \[ x_1 = x_0 + \int _0^1 v_t(x_t) \, dt, \qquad x_0 \sim p_0. \] The training process is simple: a supervised regression loss is used to match the model’s velocity prediction \( v_\theta (x, t) \) to a known target velocity field, analytically derived from the chosen coupling between source and target samples. No stochastic simulation, score estimation, or variational inference is needed.
Key Benefits:
- Fast sampling: Generates samples in tens of ODE steps rather than hundreds of reverse diffusion steps.
- Stable and interpretable training: Based on direct regression rather than variational bounds or score matching.
- Unified perspective: Recovers DDIM and other diffusion models as special cases under specific path and velocity choices.
Further Reading This section builds upon the foundational principles introduced in [364] and further elaborated in the comprehensive tutorial and codebase [363]. For visual walkthroughs and intuitive explanations, see [291, 642]. In addition to the vanilla formulation, recent works have extended Flow Matching to discrete spaces via continuous-time Markov chains [168], to Riemannian manifolds for geometry-aware modeling [86], and to general continuous-time Markov processes through Generator Matching [228]. These advances broaden the applicability of Flow Matching to diverse generative tasks. Readers are encouraged to consult these references for deeper theoretical foundations and application-specific implementations.
Enrichment 20.10.1: Generative Flows: Learning by Trajectory Integration
Motivation: From Mapping to Likelihood. Let \( p_0 \) denote a known, tractable base distribution (e.g., isotropic Gaussian), and let \( q \) denote the unknown, true data distribution. Our goal is to learn a continuous-time transformation \( \psi \) that maps \( p_0 \) to a distribution \( p_1 \approx q \). More formally, we seek a flow \( \psi : \mathbb {R}^d \to \mathbb {R}^d \) such that if \( x_0 \sim p_0 \), then \( x_1 = \psi (x_0) \sim p_1 \), and \( p_1 \) is close to \( q \) in a statistical sense.
A natural measure of this closeness is the Kullback–Leibler (KL) divergence, defined as: \[ \mathrm {KL}(q \, \| \, p_1) = \int q(x) \log \frac {q(x)}{p_1(x)} \, dx. \] Minimizing this divergence encourages the generated density \( p_1 \) to place high probability mass where the true data distribution \( q \) does. However, since \( q \) is unknown, we cannot compute this integral directly. Instead, we assume access to samples \( x \sim \tilde {q} \), where \( \tilde {q} \approx q \) is the empirical distribution defined by our dataset.
From KL to Log-Likelihood Observe that the KL divergence can be rewritten (up to an additive constant independent of \( p_1 \)) as: \[ \mathrm {KL}(q \, \| \, p_1) = -\mathbb {E}_{x \sim q} \left [ \log p_1(x) \right ] + \mathbb {E}_{x \sim q} \left [ \log q(x) \right ]. \] The second term is constant with respect to \( p_1 \), so minimizing KL is equivalent to maximizing: \[ \mathbb {E}_{x \sim \tilde {q}} \left [ \log p_1(x) \right ]. \] This is precisely the objective used in maximum likelihood estimation (MLE): we want to find parameters of the transformation \( \psi \) such that the resulting distribution \( p_1 \) assigns high likelihood to the observed data samples \( x \sim \tilde {q} \). The more likely the generated samples under \( p_1 \), the closer \( p_1 \) becomes to \( q \) in KL divergence.
How Does \( p_1 \) Arise from a Flow? Let \( \psi _t : \mathbb {R}^d \to \mathbb {R}^d \) denote a time-indexed flow map that transports samples from a known base distribution \( p_0 \) to an intermediate distribution \( p_t \), such that \( x_t = \psi _t(x_0) \) for \( x_0 \sim p_0 \). We assume \( \psi _0 = \mathrm {id} \) and that each \( \psi _t \) is a diffeomorphism—that is, smooth and invertible with a smooth inverse—for all \( t \in [0,1] \). In particular, the terminal map \( \psi _1 \) transports \( p_0 \) to a model distribution \( p_1 \), with \( x_1 = \psi _1(x_0) \sim p_1 \).
To compute or maximize the exact log-likelihood \( \log p_1(x_1) \), we must understand how the flow reshapes probability mass over time. This relationship is governed by the change-of-variables formula for differentiable bijections: \[ p_1(x_1) = p_0(x_0) \cdot \left | \det \left ( \frac {\partial \psi _1^{-1}}{\partial x_1} \right ) \right | = p_0(x_0) \cdot \left | \det \left ( \frac {\partial \psi _1}{\partial x_0} \right ) \right |^{-1}, \] where \( x_1 = \psi _1(x_0) \) and \( \frac {\partial \psi _1}{\partial x_0} \in \mathbb {R}^{d \times d} \) is the Jacobian matrix of \( \psi _1 \). The absolute value ensures volume is computed without assuming orientation. This formula follows from standard results in multivariable calculus [536, Theorem 7.26]. In practice, models often optimize the log-density form: \[ \log p_1(x_1) = \log p_0(x_0) - \log \left | \det \left ( \frac {\partial \psi _1}{\partial x_0} \right ) \right |. \]
To understand the derivation, consider a measurable region \( A \subset \mathbb {R}^d \) and its image \( B = \psi _1(A) \). Since \( \psi _1 \) is invertible, the mass over \( A \) and \( B \) must match: \[ \int _A p_0(x_0) \, dx_0 = \int _B p_1(x_1) \, dx_1. \] Changing variables in the second integral yields: \[ \int _B p_1(x_1) \, dx_1 = \int _A p_1(\psi _1(x_0)) \cdot \left | \det J_{\psi _1}(x_0) \right | \, dx_0, \] where \( J_{\psi _1}(x_0) = \frac {\partial \psi _1}{\partial x_0} \). Equating both sides and canceling the integral over \( A \) gives: \[ p_0(x_0) = p_1(\psi _1(x_0)) \cdot \left | \det J_{\psi _1}(x_0) \right |, \] and solving for \( p_1 \) recovers the change-of-variables formula.
Intuitively, this result tracks how a small volume element transforms under \( \psi _1 \). The Jacobian determinant quantifies how the flow locally scales volume: if it expands space near \( x_0 \), the mass is diluted and the density decreases at \( x_1 \); if it contracts space, the density increases. In particular: \[ \left | \det \left ( \frac {\partial \psi _1}{\partial x_0} \right ) \right | > 1 \quad \Rightarrow \quad \mbox{volume expansion, lower density,} \] \[ \left | \det \left ( \frac {\partial \psi _1}{\partial x_0} \right ) \right | < 1 \quad \Rightarrow \quad \mbox{volume compression, higher density.} \] Hence, evaluating \( p_1(x_1) \) requires tracing the pre-image \( x_0 = \psi _1^{-1}(x_1) \) and correcting the base density \( p_0(x_0) \) by the inverse local volume scaling.
While exact, this method becomes computationally burdensome in high dimensions. Computing or differentiating the Jacobian determinant of a general neural network transformation typically incurs a cost of \( \mathcal {O}(d^3) \), where \( d \) is the ambient data dimension. Unless special network structures are used—such as triangular Jacobians in RealNVP [128], invertible \(1\times 1\) convolutions in Glow [294], or Hutchinson’s trace estimators in FFJORD [185]—these costs scale poorly and introduce numerical instability during training.
To overcome this, modern approaches recast the transformation \( \psi _t \) as a solution to an ordinary differential equation (ODE) governed by a velocity field \( v_t(x) \). This continuous-time formulation allows us to express the evolution of \( \log p_t(x_t) \) in terms of divergence alone, via the probability flow ODE [87, 185, 583]. We now explore this perspective, which avoids explicit Jacobian determinants altogether.
The Role of the Continuity Equation To avoid computing high-dimensional Jacobian determinants, continuous-time flow models adopt a differential viewpoint. Instead of working directly with the global transformation \( \psi _1 \), we define a time-indexed velocity field \( v_t(x) \) that infinitesimally moves samples along trajectories \( x_t = \psi _t(x_0) \), starting from \( x_0 \sim p_0 \). The evolving distribution \( p_t \) induced by this flow changes continuously over time, and its dynamics are governed by the continuity equation: \[ \frac {\partial p_t(x)}{\partial t} + \nabla \cdot \left ( p_t(x) \, v_t(x) \right ) = 0. \] This equation formalizes the principle of local conservation of probability mass: the only way for density at a point \( x \) to change is via inflow or outflow of mass from its surrounding neighborhood.
To understand this equation precisely, let us examine the structure and roles of each term. We begin with the product \( p_t(x) \cdot v_t(x) \), often referred to as the probability flux.
Flux: Constructing \( p_t(x) v_t(x) \)
- \( p_t(x) \colon \mathbb {R}^d \to \mathbb {R} \) is a scalar field: it represents the probability density at each spatial point \( x \).
- \( v_t(x) \colon \mathbb {R}^d \to \mathbb {R}^d \) is a vector field: it assigns a velocity vector to each point in space and time.
The product \( p_t(x) v_t(x) \in \mathbb {R}^d \) is a vector-valued function defined componentwise: \[ (p_t v_t)(x) = \begin {bmatrix} p_t(x) v_{t,1}(x) \\ p_t(x) v_{t,2}(x) \\ \vdots \\ p_t(x) v_{t,d}(x) \end {bmatrix}. \] This object is called the probability flux vector field. It tells us, for each spatial coordinate direction \( i = 1, \dots , d \), the rate at which probability mass is moving through space in that direction. If the domain is \( \mathbb {R}^d \), the flux encodes how much mass is flowing through each coordinate axis — left/right, up/down, in/out — at every location and moment in time.
Intuitively, you can picture \( p_t(x) \) as the “density of fog” at point \( x \), and \( v_t(x) \) as the wind that moves the fog. Their product, \( p_t(x) v_t(x) \), describes how strongly the fog is being pushed in each direction. If the wind is fast but no fog is present, there’s no actual movement of mass. If fog is dense but wind is still, the same holds. Only when both density and velocity are present do we get mass transport.
Divergence: Understanding \( \nabla \cdot (p_t v_t) \) Despite involving the symbol \( \nabla \), the divergence operator is not a gradient. It maps a vector field \( \vec {F} : \mathbb {R}^d \to \mathbb {R}^d \) to a scalar field, and is defined as: \[ \nabla \cdot \vec {F}(x) = \sum _{i=1}^d \frac {\partial F_i(x)}{\partial x_i}. \] Applied to the flux vector \( p_t(x) v_t(x) \), we get: \[ \nabla \cdot (p_t v_t)(x) = \sum _{i=1}^d \frac {\partial }{\partial x_i} \left [ p_t(x) \cdot v_{t,i}(x) \right ]. \]
This scalar quantity captures the net rate of mass flow out of point \( x \) in all coordinate directions. For each dimension \( i \), it computes how much probability is flowing in or out through \( x_i \), and the sum tells us whether more mass is entering or exiting the region overall.
In this sense, divergence functions as a ”net-outflow meter”:
- If \( \nabla \cdot (p_t v_t)(x) > 0 \), more mass is exiting than entering — density decreases.
- If \( \nabla \cdot (p_t v_t)(x) < 0 \), more mass is arriving than leaving — density increases.
- If \( \nabla \cdot (p_t v_t)(x) = 0 \), inflow and outflow balance — density remains stable.
Unlike the gradient, which returns a vector pointing in the direction of steepest increase of a scalar field, the divergence is a scalar, that tells us whether the region is acting like a source (positive divergence) or a sink (negative divergence) of probability mass.
Putting the Continuity Equation in Plain English \[ \underbrace {\frac {\partial p_t(x)}{\partial t}}_{\mbox{\small temporal change at a fixed point}} \;+\; \underbrace {\nabla \cdot \left ( p_t(x) \, v_t(x) \right )}_{\mbox{\small net probability flowing \emph {out} of } x} \;=\; 0. \]
Think of \( p_t(x) \) as the density of a colored fog, and \( v_t(x) \) as a wind field that pushes the fog through space.
- Local accumulation: \( \displaystyle \frac {\partial p_t(x)}{\partial t} \) asks whether the fog at the fixed location \( x \) is getting thicker (\( > 0 \)) or thinner (\( < 0 \)) as time progresses. This is a temporal derivative: \( x \) is held fixed and we observe how the density changes with \( t \).
- Net inflow or outflow: \( \displaystyle \nabla \cdot \left ( p_t(x) v_t(x) \right ) \) measures the net rate at which probability mass exits an infinitesimal volume surrounding \( x \). Imagine placing a tiny box around \( x \); this term tells you how much mass escapes from the box minus how much enters it, per unit time.
The equation asserts that these two quantities exactly cancel: \[ \mbox{rate of local buildup} \;+\; \mbox{rate of escape} \;=\; 0. \]
No probability mass is created or destroyed—only transported. This is a local conservation law, the probabilistic analogue of classical principles like:
- conservation of mass in fluid dynamics,
- conservation of charge in electromagnetism.
For continuous-time generative models, the continuity equation provides a conceptual bridge between the microscopic law—how individual particles move under the velocity field \( v_t \)—and the macroscopic law—how the overall distribution \( p_t \) evolves over time.
Crucially, it allows us to reason about global changes in the distribution without explicitly computing expensive Jacobian determinants: the continuity equation already captures the effect of the full flow through a compact, pointwise identity.
Broader Implications for Continuous-Time Generative Models The continuity equation \[ \frac {\partial p_t(x)}{\partial t} + \nabla \cdot \left ( p_t(x)\,v_t(x) \right ) = 0 \tag {CE} \] is the probabilistic analogue of mass conservation in fluid dynamics. Any continuous-time generative model that defines trajectories via the ODE \[ \frac {d}{dt} x_t = v_t(x_t) \] must respect this equation to ensure that probability mass is preserved under the flow. Notable examples include Neural ODEs [87], FFJORD [185], and probability flow ODEs [583].
One of the most important consequences of this formulation is that it allows us to track the evolution of the log-density along a sample trajectory \( x_t \) without computing high-dimensional Jacobian determinants.
Step-by-step: How Log-Density Evolves Along the Flow
Let \( x_t \) be the solution to the ODE \( \dot {x}_t = v_t(x_t) \). To understand how the density \( p_t(x_t) \) changes along this trajectory, we apply the chain rule for total derivatives to the composition \( t \mapsto \log p_t(x_t) \): \[ \frac {d}{dt} \log p_t(x_t) = \underbrace {\frac {\partial }{\partial t} \log p_t(x)}_{\mbox{explicit time dependence}} + \underbrace {\nabla _x \log p_t(x) \cdot \frac {d x_t}{dt}}_{\mbox{motion along the path}} \bigg |_{x = x_t}. \] The first term captures how the log-density at a fixed spatial location changes over time. The second term accounts for how the log-density changes as the point \( x_t \) moves through space.
We now turn to the continuity equation: \[ \frac {\partial p_t(x)}{\partial t} + \nabla \cdot \left ( p_t(x)\,v_t(x) \right ) = 0. \] Assuming \( p_t(x) > 0 \), we divide through by \( p_t(x) \) to rewrite the equation in terms of \( \log p_t(x) \): \[ \frac {1}{p_t(x)} \frac {\partial p_t(x)}{\partial t} + \frac {1}{p_t(x)} \nabla \cdot \left ( p_t(x)\,v_t(x) \right ) = 0. \]
Using the identities: \[ \frac {\partial }{\partial t} \log p_t(x) = \frac {1}{p_t(x)} \frac {\partial p_t(x)}{\partial t}, \qquad \nabla \cdot \left ( p_t v_t \right ) = \nabla p_t \cdot v_t + p_t \nabla \cdot v_t, \] we substitute and rearrange: \[ \frac {\partial }{\partial t} \log p_t(x) = - \nabla \cdot v_t(x) - \nabla _x \log p_t(x) \cdot v_t(x). \]
Substituting this into the total derivative expression (and using \( \dot {x}_t = v_t(x_t) \)) gives: \[ \frac {d}{dt} \log p_t(x_t) = \left [ - \nabla \cdot v_t(x) - \nabla _x \log p_t(x) \cdot v_t(x) \right ] + \nabla _x \log p_t(x) \cdot v_t(x) \bigg |_{x = x_t}. \] The inner product terms cancel, leaving: \[ \frac {d}{dt} \log p_t(x_t) = - \nabla \cdot v_t(x_t). \]
This is the celebrated Liouville identity, which relates log-density dynamics to the divergence of the velocity field: \begin {equation} \boxed { \frac {d}{dt} \log p_t(x_t) = - \nabla \cdot v_t(x_t) } \end {equation}
Interpretation This equation reveals that the rate of change of log-density along the path of a particle is governed entirely by the local divergence of the velocity field at that point. If \( \nabla \cdot v_t > 0 \), the flow is expanding locally: volumes grow, so density must decrease. If \( \nabla \cdot v_t < 0 \), the flow is compressing: volumes shrink, so density increases. Hence, divergence acts as a local proxy for log-likelihood adjustment.
From here, we can integrate both sides over time to obtain an exact log-likelihood formula for a sample transformed through the flow: \[ \log p_1(x_1) = \log p_0(x_0) - \int _0^1 \nabla \cdot v_t(x_t) \, dt, \qquad x_1 = \psi _1(x_0). \] This shows that to evaluate \( \log p_1(x_1) \), we simply need to know the base log-density \( \log p_0(x_0) \) and integrate the divergence along the trajectory. No determinant or inverse map is needed.
This identity is the foundation of continuous normalizing flows (CNFs)—a class of generative models that define invertible mappings by continuously transforming a base distribution \( p_0 \) via a learned differential equation \( \frac {d}{dt} x_t = v_t(x_t) \).
CNFs generalize discrete normalizing flows by replacing sequences of invertible layers with a smooth velocity field, and they compute log-likelihoods exactly via the Liouville identity. This makes maximum-likelihood training in continuous-time models theoretically elegant and tractable, using numerical ODE solvers to trace sample trajectories and trace estimators (e.g., Hutchinson’s method) to approximate divergence.
Why Pure CNF–Likelihood Training Is Not Scalable? The Liouville identity provides an exact formula for the model likelihood in continuous-time generative models governed by an ODE \( \dot {x}_t = v_t(x_t) \): \[ \log p_1(x_1) = \log p_0(x_0) - \int _0^1 \nabla \cdot v_t(x_t) \, dt, \qquad x_1 = \psi _1(x_0). \] In theory, this makes continuous normalizing flows (CNFs) ideal candidates for maximum likelihood estimation. For a dataset of samples \( \{ x^{(i)}_{\mbox{data}} \} \), one could train the model by maximizing this likelihood with respect to the parameters of \( v_t \), using standard gradient-based optimization.
How training works in principle:
- 1.
- Reverse ODE step: For each data point \( x_1 = x^{(i)}_{\mbox{data}} \), solve the reverse-time ODE \[ \frac {d}{dt} x_t = -v_{1 - t}(x_t) \] backward from \( t = 1 \) to \( t = 0 \), yielding the latent code \( x_0 = \psi _1^{-1}(x_1) \).
- 2.
- Divergence accumulation: Along this trajectory, compute or estimate the integral \[ \int _0^1 \nabla \cdot v_t(x_t) \, dt \] using numerical quadrature.
- 3.
- Likelihood computation: Combine with the known base density \( p_0(x_0) \) to evaluate \[ \log p_1(x_1) = \log p_0(x_0) - \int _0^1 \nabla \cdot v_t(x_t) \, dt. \]
- 4.
- Optimization: Backpropagate through all of the above to update the parameters of \( v_t \) to maximize the total log-likelihood over the dataset.
While theoretically elegant, this “textbook” maximum likelihood strategy faces major barriers in practice—especially when scaling to high-dimensional data such as natural images.
Where the computational cost comes from:
- 1.
- Trajectory integration. Every forward (or reverse) pass requires numerically solving the ODE \( \dot {x}_t = v_t(x_t) \) over \( t \in [0,1] \). Adaptive solvers like Runge–Kutta may need 30–200 function evaluations, depending on the stiffness and complexity of \( v_t \).
- 2.
- Divergence computation. The divergence \( \nabla \cdot v_t(x_t) \) is the trace of the Jacobian \( \nabla _x v_t \in \mathbb {R}^{d \times d} \). Estimating this exactly costs \( \mathcal {O}(d^2) \), or up to \( \mathcal {O}(d^3) \) with autodiff. Hutchinson’s stochastic trace estimator [185] reduces the cost to \( \mathcal {O}(d) \) but introduces variance that must be averaged out over multiple random vectors.
- 3.
- Backpropagation. Training requires gradients of the loss with respect to the parameters of \( v_t \), which depends on the full trajectory. This necessitates differentiating through the ODE solver. Adjoint sensitivity methods [87] reduce memory use, but can be numerically unstable and roughly double the runtime.
- 4.
- Slow sampling. Unlike discrete normalizing flows, CNFs require solving the forward ODE \( \dot {x}_t = v_t(x_t) \) even at inference time for each latent \( x_0 \sim p_0 \). Sampling is thus orders of magnitude slower than a feedforward network.
Additionally: score-based dependencies. Some continuous-time models incorporate score terms \( \nabla _x \log p_t(x) \), either to guide learning or to define velocity fields indirectly. These score functions are difficult to estimate robustly in high dimensions and often lead to unstable gradients or high variance during training.
Modern practice. Because of these practical limitations, state-of-the-art CNF-based models often avoid direct maximum likelihood training altogether:
- FFJORD [185] uses Hutchinson’s trick to estimate the divergence efficiently, but is still limited to low-resolution datasets like CIFAR-10 (\( 32 \times 32 \)).
- Probability flow ODEs [583] sidestep likelihood computation during training by learning the score function \( \nabla _x \log p_t(x) \) using denoising score-matching losses. The ODE is only used at test time for generation.
- Hybrid methods perform training with diffusion-style objectives and sample deterministically with few ODE steps (as in DDIM or ODE-based sampling), achieving good sample quality at lower cost.
Flow Matching: A New Approach While the Liouville identity enables exact likelihood estimation in continuous normalizing flows (CNFs), its practical use is limited by the computational cost of integrating trajectories, estimating divergence, and backpropagating through ODE solvers—especially in high-dimensional settings like natural images.
This leads to a natural question:
Can we avoid computing densities or their derivatives—and directly learn how to transport mass from \( p_0 \) to \( p_1 \)?
Flow Matching [364] answers this affirmatively. It reframes generative modeling as supervised learning over velocity fields—sidestepping the need for log-densities, Jacobians, or variational objectives.
Given pairs \( x_0 \sim p_0 \) and \( x_1 \sim p_1 \), a target velocity field \(v_t(x)\) is computed analytically based on a known interpolation path. A neural network is then trained to match this field by pointwise regression. The key advantages:
- No divergence or Jacobian evaluation is needed.
- No density estimation or score functions are involved.
- No integration of log-likelihoods or backward ODEs is required.
By directly learning how probability flows, Flow Matching enforces the continuity equation in a weak, sample-based sense—yielding a scalable alternative to CNFs for modern generative tasks.
Enrichment 20.10.2: Development of the Flow Matching Objective
From Density Path to Vector Field The Flow Matching objective is rooted in the relationship between a time-evolving probability distribution \( \{p_t(x)\}_{t \in [0,1]} \) and the velocity field \( u_t(x) \) that transports mass along this path. This relationship is formalized by the continuity equation: \[ \frac {\partial p_t(x)}{\partial t} + \nabla \cdot \left ( p_t(x) u_t(x) \right ) = 0. \] This PDE expresses local conservation of probability mass: the change in density at a point is exactly offset by the net flow of mass in or out.
Crucially, this equation not only constrains \( u_t \) when \( p_t \) and \( u_t \) are given jointly—it can also be used in reverse: if we specify a smooth and differentiable path of densities \( p_t(x) \), then there exists a corresponding velocity field \( u_t(x) \) that satisfies this equation. In fact, \( u_t(x) \) is uniquely determined (up to divergence-free components) by solving the inverse problem: \[ \nabla \cdot (p_t(x) u_t(x)) = -\frac {\partial p_t(x)}{\partial t}. \]
Under appropriate regularity conditions, this equation has a constructive solution. In particular, one can use it to show that the velocity field \( u_t(x) \) can be expressed as: \[ u_t(x) = -\nabla \log p_t(x) + \frac {\nabla p_t(x)}{p_t(x)} - \frac {\partial _t p_t(x)}{p_t(x)} \cdot \nabla ^{-1}, \] where \( \nabla ^{-1} \) denotes the formal inverse divergence operator (e.g., via solving a Poisson equation). While this expression may not always be tractable to compute directly, it conceptually shows that \( u_t \) is entirely determined by \( p_t \) and its derivatives.
This insight is the foundation of Flow Matching: if the path \( p_t \) is known or constructed, the generating vector field \( u_t \) is fixed by the continuity equation. Thus, in principle, one can train a neural network \( v_\theta (t, x) \) to match this true transport field using supervised learning.
The Naive Flow Matching Objective This motivates the general Flow Matching training loss: \[ \mathcal {L}_{\mathrm {FM}}(\theta ) = \mathbb {E}_{t \sim \mathcal {U}[0,1],\, x \sim p_t} \left [ \|v_\theta (t, x) - u_t(x)\|^2 \right ], \tag {FM-naive} \] where:
- \( v_\theta (t,x) \) is a learnable velocity field (e.g., a neural network with parameters \( \theta \)),
- \( u_t(x) \) is the ground-truth velocity field that satisfies the continuity equation for the path \( \{p_t\} \),
- \( x \sim p_t \) denotes that samples are drawn from the intermediate distribution at time \( t \),
- \( t \sim \mathcal {U}[0,1] \) is sampled uniformly across time.
Intuitively, this objective trains the CNF vector field \( v_\theta \) to reproduce the flow that transports the mass of \( p_0 \) to \( p_1 \) via the path \( \{p_t\} \). If the regression error reaches zero, then integrating \( v_\theta \) over time from \( t=0 \) to \( t=1 \) recovers the exact map \( \psi _t \) that generates the full path, including the final distribution \( p_1(x) \approx q(x) \).
Why the Naive Objective Is Intractable While the Flow Matching loss provides a clean supervised objective, applying it naively in practice proves infeasible. The loss \[ \mathcal {L}_{\mathrm {FM}}(\theta ) = \mathbb {E}_{t \sim \mathcal {U}[0,1],\, x \sim p_t} \left [ \|v_\theta (t, x) - u_t(x)\|^2 \right ] \] assumes access to both the intermediate density \( p_t \) and the corresponding vector field \( u_t \) at every point in space and time. But in real-world generative modeling settings, neither of these quantities is known in closed form.
First, the interpolation path \( \{p_t\} \) is fundamentally underdetermined: there are infinitely many ways to transition from \( p_0 \) to \( p_1 \), each leading to a different transport behavior. Whether we interpolate linearly in sample space, follow heat diffusion, or traverse a Wasserstein geodesic, each path implies a different evolution of probability mass—and a different target field \( u_t \).
Even if we fix a reasonable interpolation scheme, we still face two practical barriers:
- We typically cannot sample from \( p_t(x) \) at arbitrary times.
- We cannot compute \( u_t(x) \), since it involves inverting the continuity equation—a PDE that depends on time derivatives and spatial gradients of \( p_t \).
In short, the general form of the FM loss assumes a full global picture of how mass moves from \( p_0 \) to \( p_1 \)—but in practice, we only have endpoint samples: \( x_0 \sim p_0 \) (a known prior) and \( x_1 \sim p_1 \approx q(x) \) (empirical data). We know nothing about the intermediate distributions \( p_t \), nor their generating vector fields.
A Local Solution via Conditional Paths To sidestep the intractability of directly modeling a global interpolation path \( \{p_t(x)\} \) and its corresponding velocity field \( u_t(x) \), Flow Matching proposes a local, sample-driven construction. The core idea is to replace the global perspective with conditional trajectories: we define a family of conditional probability paths \( p_t(x \mid x_1) \), each anchored at a target point \( x_1 \sim p_1 \approx q(x) \). These conditional paths describe how probability mass should evolve from a shared base distribution \( p_0 \) toward individual endpoints \( x_1 \), using analytically tractable trajectories.
How are these conditional paths designed? Each path \( p_t(x \mid x_1) \) is constructed to satisfy the continuity equation with an explicit, closed-form velocity field \( u_t(x \mid x_1) \). Importantly, the family is required to obey two boundary conditions: \[ p_0(x \mid x_1) = p_0(x), \qquad p_1(x \mid x_1) \approx \delta (x - x_1). \] The first condition ensures that all paths begin from the same tractable prior \( p_0 \), independent of \( x_1 \). The second condition encodes that each conditional flow must concentrate around its destination. In practice, since the Dirac delta \( \delta (x - x_1) \) is not a true probability density, we approximate it using a sharply peaked Gaussian: \[ p_1(x \mid x_1) = \mathcal {N}(x \mid x_1, \sigma ^2 I), \quad \mbox{for small } \sigma > 0. \] This reflects the intuition that the flow transitions from initial noise to a highly concentrated distribution centered at \( x_1 \) as \( t \to 1 \). All mass should converge to \( x_1 \), with negligible uncertainty.
From Conditional Paths to a Marginal Distribution. To construct a global flow from sample-wise supervision, Flow Matching defines a marginal density path \( p_t(x) \) as a mixture of conditional flows: \[ p_t(x) = \int p_t(x \mid x_1)\, q(x_1)\, dx_1. \] This corresponds to Equation (6) in the original Flow Matching paper.
This integral represents the total probability mass at point \( x \) and time \( t \), as aggregated over all conditional trajectories, each targeting a different data point \( x_1 \sim q \). At the final time step \( t = 1 \), this becomes: \[ p_1(x) = \int p_1(x \mid x_1)\, q(x_1)\, dx_1, \] which can be made arbitrarily close to the true data distribution \( q(x) \) by choosing each terminal conditional \( p_1(x \mid x_1) \) to concentrate sharply around \( x_1 \), e.g., using a small-variance Gaussian. This mixture construction enables a natural approximation of the data distribution through analytically controlled flows.
Recovering the Marginal Vector Field Having defined the marginal path \( p_t(x) \) as a mixture of conditional densities: \[ p_t(x) = \int p_t(x \mid x_1)\, q(x_1)\, dx_1, \] it is natural to ask: can we recover the corresponding marginal velocity field \( u_t(x) \) from the family of conditional vector fields \( u_t(x \mid x_1) \) that generate each conditional path?
The answer is yes. A key result from the Flow Matching paper shows that we can construct the marginal velocity field as: \[ u_t(x) = \frac {1}{p_t(x)} \int u_t(x \mid x_1)\, p_t(x \mid x_1)\, q(x_1)\, dx_1. \] This is Equation (8) in the Flow Matching paper.
Intuitively, this tells us that the velocity at point \( x \) is the average of all conditional vector fields evaluated at \( x \), weighted by how much probability mass each conditional contributes there. In probabilistic terms, this expression can be rewritten as: \[ u_t(x) = \mathbb {E}[\, u_t(X_t \mid X_1) \mid X_t = x \,], \] where \( (X_t, X_1) \sim p_t(x \mid x_1)\, q(x_1) \). That is, \( u_t(x) \) represents the expected direction of flow at location \( x \), aggregated across all conditionals that pass through \( x \) at time \( t \).
Why This Identity Is Valid The expression \[ u_t(x) = \frac {1}{p_t(x)} \int u_t(x \mid x_1)\, p_t(x \mid x_1)\, q(x_1)\, dx_1 \] is not just a useful identity—it is mathematically necessary if we want the marginal path \( p_t(x) \) to satisfy the continuity equation with respect to a single global vector field \( u_t(x) \). This result is formalized as Theorem 1 in the Flow Matching paper [364], which states:
If each conditional pair \( (p_t(x \mid x_1), u_t(x \mid x_1)) \) satisfies the continuity equation, then the marginal pair defined by \[ p_t(x) = \int p_t(x \mid x_1)\, q(x_1)\, dx_1, \qquad u_t(x) = \frac {1}{p_t(x)} \int u_t(x \mid x_1)\, p_t(x \mid x_1)\, q(x_1)\, dx_1 \] also satisfies the continuity equation: \[ \frac {\partial p_t(x)}{\partial t} + \nabla \cdot (p_t(x)\, u_t(x)) = 0. \]
We now sketch the intuition behind this result. Starting from the conditional continuity equation: \[ \frac {\partial p_t(x \mid x_1)}{\partial t} + \nabla \cdot \left (p_t(x \mid x_1)\, u_t(x \mid x_1)\right ) = 0, \] we multiply both sides by \( q(x_1) \) and integrate over \( x_1 \): \[ \int \frac {\partial p_t(x \mid x_1)}{\partial t} \, q(x_1)\, dx_1 + \int \nabla \cdot \left (p_t(x \mid x_1)\, u_t(x \mid x_1)\right ) q(x_1)\, dx_1 = 0. \] Assuming regularity (so that we can exchange integration and differentiation), this gives: \[ \frac {\partial }{\partial t} \left ( \int p_t(x \mid x_1)\, q(x_1)\, dx_1 \right ) + \nabla \cdot \left ( \int p_t(x \mid x_1)\, u_t(x \mid x_1)\, q(x_1)\, dx_1 \right ) = 0. \]
Now we invoke the definition of the marginal density: \[ p_t(x) := \int p_t(x \mid x_1)\, q(x_1)\, dx_1. \] This tells us that the first term becomes \( \partial _t p_t(x) \). However, the second term is not yet in the standard continuity form \( \nabla \cdot (p_t(x)\, u_t(x)) \). To get there, we introduce a definition for the marginal velocity field: \[ p_t(x)\, u_t(x) := \int p_t(x \mid x_1)\, u_t(x \mid x_1)\, q(x_1)\, dx_1. \] This is a definition, not a derived fact. It says: let \( u_t(x) \) be the vector such that when multiplied by \( p_t(x) \), it reproduces the total flux across all conditionals.
Substituting this into the continuity equation yields: \[ \frac {\partial p_t(x)}{\partial t} + \nabla \cdot (p_t(x)\, u_t(x)) = 0, \] which is exactly the continuity equation for the marginal trajectory.
In short: given conditional flows \( u_t(x \mid x_1) \) that preserve mass individually, the only way to define a global velocity field \( u_t(x) \) that preserves mass along the marginal trajectory is to aggregate the flux contributions and normalize by \( p_t(x) \). For the full formal proof, see Appendix A of [364].
From Validity to Practicality: The Need for a Tractable Objective While the marginalization identity is theoretically elegant—it expresses \( u_t(x) \) as a weighted average over analytically defined conditional fields—it remains fundamentally impractical for training. The core issue lies in its reliance on the marginal density \( p_t(x) \), which is defined by: \[ p_t(x) = \int p_t(x \mid x_1)\, q(x_1)\, dx_1. \] This expression depends on the true data distribution \( q(x_1) \), which we only observe through samples, and involves high-dimensional integration over all conditional paths. As a result, both evaluating \( u_t(x) \) and sampling from \( p_t(x) \) are intractable in practice.
Hence, the original Flow Matching loss, \[ \mathcal {L}_{\mathrm {FM}} = \mathbb {E}_{t, x \sim p_t} \left [ \| v_\theta (t, x) - u_t(x) \|^2 \right ], \] is still inaccessible for direct optimization. Even though each conditional pair \( (p_t(x \mid x_1), u_t(x \mid x_1)) \) can be formed analytically tractable and mass-preserving, their integration into the marginal field \( u_t(x) \) requires quantities we cannot reliably compute.
Conditional Flow Matching (CFM): A Sample-Based Reformulation The intractability of evaluating the marginal field \( u_t(x) \) in the original Flow Matching loss motivates a powerful reformulation: rather than matching the marginal flow \( u_t(x) \), can we train a model to match the conditional vector fields \( u_t(x \mid x_1) \), which are analytically known?
This is the central idea behind Conditional Flow Matching (CFM). Instead of supervising the model using the marginal loss: \[ \mathcal {L}_{\mathrm {FM}} = \mathbb {E}_{t,\, x \sim p_t(x)} \left [ \| v_\theta (t, x) - u_t(x) \|^2 \right ], \] which depends on the inaccessible \( u_t(x) \), we define a new, tractable conditional loss: \[ \boxed { \mathcal {L}_{\mathrm {CFM}} = \mathbb {E}_{t \sim \mathcal {U}[0,1],\, x_1 \sim q,\, x \sim p_t(x \mid x_1)} \left [ \| v_\theta (t, x, x_1) - u_t(x \mid x_1) \|^2 \right ] } \]
Every term in this expression is fully accessible:
- \( x_1 \sim q \): empirical samples from the data distribution.
- \( p_t(x \mid x_1) \): an analytically chosen, time-dependent conditional path (to be introduced next).
- \( u_t(x \mid x_1) \): the closed-form velocity field derived from that conditional path.
In this section we do not yet commit to a specific form of \( p_t(x \mid x_1) \), but crucially, the framework allows any analytic choice—so long as it satisfies appropriate boundary conditions and yields a velocity field computable in closed form. In the next section, we explore such constructions explicitly.
Why is this valid? The equivalence between CFM and the original FM objective is formalized in Theorem 2 of the Flow Matching paper [364], which states:
Assuming \( p_t(x) > 0 \) for all \( x \in \mathbb {R}^d \) and \( t \in [0, 1] \), and under mild regularity assumptions, the conditional loss \( \mathcal {L}_{\mathrm {CFM}} \) and the marginal loss \( \mathcal {L}_{\mathrm {FM}} \) have identical gradients with respect to \( \theta \): \[ \nabla _\theta \mathcal {L}_{\mathrm {CFM}} = \nabla _\theta \mathcal {L}_{\mathrm {FM}}. \]
The proof relies on rewriting both losses using bilinearity of the squared norm, and applying Fubini’s Theorem to swap the order of integration over \( x \) and \( x_1 \). The core insight is that the marginal field \( u_t(x) \) is itself an average over the conditional fields \( u_t(x \mid x_1) \), making CFM an unbiased surrogate for the original objective. For a detailed derivation, see Appendix A of [364].
Why This Is Powerful The Conditional Flow Matching objective unlocks a practical and scalable method for training continuous-time generative models. It removes the need to estimate intermediate marginals or evaluate global velocity fields—obstacles that make the original FM loss intractable in high dimensions.
Moreover, this framework is highly flexible: so long as we define a valid conditional path \( p_t(x \mid x_1) \) with known boundary conditions and an analytic velocity field \( u_t(x \mid x_1) \), we can train a model using only endpoint samples \( (x_0, x_1) \sim p_0 \times q \). This enables a wide variety of conditional designs, each inducing distinct training behavior and inductive biases.
In the next part, we introduce several tractable and theoretically grounded choices for the conditional trajectory \( p_t(x \mid x_1) \) and its corresponding vector field \( u_t(x \mid x_1) \), including Gaussian interpolants and optimal transport-inspired paths.
Enrichment 20.10.3: Conditional Probability Paths and Vector Fields
Motivation The core idea of Flow Matching is to train a learnable velocity field \( v_\theta (t, x) \) by supervising it with analytically defined transport dynamics. Instead of attempting to construct a global flow that maps an entire distribution \( p_0 \) into \( p_1 \), we take a more tractable approach: we define conditional flows from the base distribution \( p_0 \) to individual target points \( x_1 \sim q \). This formulation enables both analytic expressions for the evolving conditional densities \( p_t(x \mid x_1) \) and closed-form velocity fields \( u_t(x \mid x_1) \), making the learning objective fully traceable.
In principle, many choices of conditional probability paths are valid—ranging from Gaussian bridges to more complex nonlinear interpolants—so long as they satisfy the required boundary conditions and preserve mass via the continuity equation. In what follows, we focus on one particularly convenient and expressive family: Gaussian conditional paths. These offer a balance of mathematical simplicity, closed-form expressions, and intuitive behavior, making them a canonical starting point for Conditional Flow Matching.
Canonical Gaussian Conditional Paths We begin with a simple yet expressive family of conditional probability paths: \[ p_t(x \mid x_1) = \mathcal {N}(x \mid \mu _t(x_1), \sigma _t^2 I), \qquad \mu _t(x_1) = t x_1, \quad \sigma _t^2 = (1 - t)^2. \]
This path evolves from the standard Gaussian base \( p_0(x) = \mathcal {N}(0, I) \) to the terminal distribution \( p_1(x \mid x_1) = \delta (x - x_1) \), satisfying the boundary conditions: \[ p_0(x \mid x_1) = p_0(x), \qquad p_1(x \mid x_1) = \delta (x - x_1). \]
The design is intuitive:
- The mean \( \mu _t(x_1) = t x_1 \) moves linearly from the origin to the target \( x_1 \).
- The variance \( \sigma _t^2 = (1 - t)^2 \) shrinks quadratically to zero, causing the distribution to contract into a point mass at \( x_1 \) as \( t \to 1 \).
This makes it an ideal conditional flow for modeling reverse diffusion processes.
Deriving the Velocity Field from the Continuity Equation Using the continuity equation, \[ \frac {\partial }{\partial t} p_t(x \mid x_1) + \nabla \cdot \left ( p_t(x \mid x_1) \cdot u_t(x \mid x_1) \right ) = 0, \] we can solve for the velocity field that generates this flow. Since both the time derivative and spatial divergence of a Gaussian are available in closed form, the solution is: \[ u_t(x \mid x_1) = \frac {x_1 - x}{1 - t}. \]
This velocity points linearly from the current location \( x \) to the target \( x_1 \), with increasing strength as time progresses. As \( t \to 1 \), the velocity diverges—ensuring all mass arrives precisely at \( x_1 \), in accordance with the boundary condition \( p_1(x \mid x_1) = \delta (x - x_1) \).
This canonical path illustrates the simplest form of analytically traceable conditional flow—where both the density and velocity field are closed-form, and probability mass moves deterministically from noise to data.
General Gaussian Conditional Paths and Affine Flow Maps The linear trajectory described above is a special case of a broader class of flows. Conditional Flow Matching accommodates any family of Gaussian conditionals: \[ p_t(x \mid x_1) = \mathcal {N}(x \mid \mu _t(x_1), \sigma _t^2(x_1) I), \] where:
- \( \mu _t(x_1) \colon [0,1] \times \mathbb {R}^d \to \mathbb {R}^d \) is a time-dependent mean schedule,
- \( \sigma _t(x_1) > 0 \) is a smooth variance schedule.
We require the boundary conditions: \[ \mu _0(x_1) = 0, \quad \sigma _0(x_1) = 1, \qquad \mu _1(x_1) = x_1, \quad \sigma _1(x_1) \to 0, \] so that the paths begin at standard Gaussian noise and converge toward the target \( x_1 \). The canonical example from above corresponds to the specific case: \[ \mu _t(x_1) = t x_1, \qquad \sigma _t(x_1) = 1 - t. \]
The Canonical Affine Flow and Induced Velocity Field To describe how conditional samples evolve over time, we define an explicit transport map that pushes noise to data. This map is affine in form: \[ \psi _t(x_0) = \sigma _t(x_1) x_0 + \mu _t(x_1), \] where \( x_0 \sim \mathcal {N}(0, I) \) is a standard Gaussian sample. The function \( \psi _t \) deterministically transports \( x_0 \) to \( x \sim p_t(x \mid x_1) \), and is invertible for all \( t \in [0, 1) \) as long as \( \sigma _t(x_1) > 0 \). Under this map, the pushforward satisfies: \[ [\psi _t]_*(\mathcal {N}(0, I)) = \mathcal {N}(x \mid \mu _t(x_1), \sigma _t^2(x_1) I) = p_t(x \mid x_1), \] which ensures that the conditional path \( p_t(x \mid x_1) \) evolves according to a known distribution family.
To derive the velocity field that generates this flow, we differentiate \( \psi _t(x_0) \) with respect to time: \[ \frac {d}{dt} \psi _t(x_0) = \sigma _t'(x_1)\, x_0 + \mu _t'(x_1), \] which describes how points in latent (noise) space evolve over time. However, to express the velocity field \( u_t(x \mid x_1) \) in data space, we must write this in terms of \( x = \psi _t(x_0) \), not \( x_0 \). Since the map is invertible, we isolate the preimage: \[ x_0 = \frac {x - \mu _t(x_1)}{\sigma _t(x_1)}, \] and substitute back to obtain: \[ u_t(x \mid x_1) = \frac {d}{dt} \psi _t(x_0) = \sigma _t'(x_1) \cdot \frac {x - \mu _t(x_1)}{\sigma _t(x_1)} + \mu _t'(x_1), \] which simplifies to: \[ u_t(x \mid x_1) = \frac {\sigma _t'(x_1)}{\sigma _t(x_1)} (x - \mu _t(x_1)) + \mu _t'(x_1). \tag {CFM-velocity} \]
Interpretation. This expression reveals two complementary effects:
- The term \( (x - \mu _t(x_1)) \cdot \frac {\sigma _t'}{\sigma _t} \) describes how samples are pulled toward the evolving mean as the variance decays—capturing contraction of the distribution.
- The term \( \mu _t'(x_1) \) captures the drift of the mean itself, i.e., how the center of the distribution moves over time.
Together, these components define the precise trajectory of mass under the affine Gaussian flow: a contraction toward the target \( x_1 \) combined with translation along a smooth path. The result guarantees mass conservation and adherence to the conditional boundary conditions \( p_0(x \mid x_1) = p_0(x) \) and \( p_1(x \mid x_1) \to \delta (x - x_1) \) as \( \sigma _1 \to 0 \).
This derivation is formalized in Theorem 3 of the Flow Matching Guide, with a full proof provided in Appendix A.
The Conditional Flow Matching Loss Once we define the affine flow map \( \psi _t(x_0) = \sigma _t(x_1) x_0 + \mu _t(x_1) \), and obtain its time derivative \( \frac {d}{dt} \psi _t(x_0) = \sigma _t'(x_1) x_0 + \mu _t'(x_1) \), we can directly supervise the learnable velocity field \( v_\theta \) by comparing it to the known transport dynamics.
This gives rise to the Conditional Flow Matching (CFM) objective: \[ \mathcal {L}_{\mathrm {CFM}}(\theta ) = \mathbb {E}_{x_1 \sim q,\, x_0 \sim \mathcal {N}(0, I),\, t \sim \mathcal {U}[0,1]} \left \| v_\theta (t, \psi _t(x_0)) - \frac {d}{dt} \psi _t(x_0) \right \|^2, \tag {CFM-loss} \] which corresponds to Equation (13) in the original Flow Matching paper [364].
Why this works: The key idea is to reparameterize the regression problem from data space into latent (noise) space, where samples \( x \sim p_t(x \mid x_1) \) are expressed as \( x = \psi _t(x_0) \). Since \( x_0 \sim \mathcal {N}(0, I) \) and \( x_1 \sim q \) are both directly sampleable, this makes the objective entirely traceable. The CFM loss thus replaces intractable expectations over marginal densities (as in the original FM loss) with analytic supervision along known deterministic trajectories.
From Theory to Practice: Training with Conditional Flow Matching We now summarize how the Conditional Flow Matching (CFM) framework translates into an efficient, fully traceable training algorithm. Recall that our supervised objective is:
\[ \mathcal {L}_{\mathrm {CFM}}(\theta ) = \mathbb {E}_{t \sim \mathcal {U}[0,1],\, x_1 \sim q,\, x_0 \sim \mathcal {N}(0, I)} \left \| v_\theta (t, \psi _t(x_0)) - \frac {d}{dt} \psi _t(x_0) \right \|^2. \tag {CFM-loss} \]
This formulation enables gradient-based optimization using only sample pairs from \( q \) and \( p_0 = \mathcal {N}(0, I) \), along with the known closed-form target velocity field. We now describe the training loop explicitly.
- Sample minibatch of data: \( \{x_1^{(i)}\}_{i=1}^B \sim q \)
-
For each sample:
- Sample time \( t \sim \mathcal {U}([0,1]) \)
- Sample noise vector \( x_0^{(i)} \sim \mathcal {N}(0, I) \)
- Compute interpolated point: \[ x_t^{(i)} = \psi _t(x_0^{(i)} \mid x_1^{(i)}) = \sigma _t(x_1^{(i)}) \, x_0^{(i)} + \mu _t(x_1^{(i)}) \]
- Compute target velocity: \[ \dot {x}^{(i)} = \frac {d}{dt} \psi _t(x_0^{(i)}) = \sigma _t'(x_1^{(i)}) \, x_0^{(i)} + \mu _t'(x_1^{(i)}) \]
- Compute batch loss: \[ \mathcal {L}_{\mbox{CFM}}(\theta ) = \frac {1}{B} \sum _{i=1}^B \left \| v_\theta (t, x_t^{(i)}, x_1^{(i)}) - \dot {x}^{(i)} \right \|^2 \]
- Update model parameters \( \theta \) via gradient descent.
- Natural Extension to Images: Conditional Flow Matching is particularly well-suited to image generation. In this setting, both noise samples \( x_0 \) and target data \( x_1 \) are tensors of shape \( \mathbb {R}^{C \times H \times W} \) (e.g., \( 3 \times 64 \times 64 \)). The learned velocity field \( v_\theta (t, x, x_1) \) is implemented as a time-conditioned convolutional neural network that predicts a velocity tensor of the same shape. During training, the model learns how to morph isotropic Gaussian noise into sharp, structured images.
- Sample-Based Supervision: Training involves sampling a triplet \( (x_0, x_1, t) \), computing \( x = \psi _t(x_0 \mid x_1) \), and supervising \( v_\theta \) to match the analytic flow velocity \( \frac {d}{dt} \psi _t(x_0) \). For instance, with the canonical Gaussian path, the model learns to push blurry noise blobs into semantically coherent images over time.
-
Efficient Data Pipeline: There is no need to evaluate densities or simulate stochastic trajectories. Each sample is generated in a single forward pass using the affine flow map \( \psi _t \). This allows for efficient minibatch training using standard image augmentation pipelines.
- Avoiding Score Estimation: Unlike diffusion models that require regressing to noisy gradients \( \nabla _x \log p_t(x) \), CFM provides an explicit, closed-form supervision target. This sidesteps the need for score networks or denoising-based estimators, which are often difficult to tune and computationally expensive.
- No Marginal Modeling Required: Importantly, the global marginal distribution \( p_t(x) \) is never required—neither for sampling nor for loss evaluation. This makes CFM far easier to scale to high-dimensional outputs like images, where intermediate marginals are intractable to estimate or store.
- Flexible Trajectories: The affine flow map \( \psi _t(x_0) = \sigma _t(x_1)\, x_0 + \mu _t(x_1) \) allows for expressive and interpretable design of the probability paths. For instance, one can interpolate linearly toward the data, or follow an optimal transport displacement. These different trajectories influence not only the flow geometry, but also how sharp or smooth the intermediate samples appear during training.
This sample-driven, closed-form supervision strategy makes Conditional Flow Matching highly effective for learning smooth transitions from noise to data—particularly in structured domains like image synthesis. In the next section, we explore concrete flow designs using schedules \( \mu _t(x_1) \) and \( \sigma _t(x_1) \) that recover known diffusion processes and optimal transport flows as special cases.
Summary Conditional Flow Matching offers a rare combination of theoretical rigor and computational simplicity. The model learns directly from known flows between isotropic noise and real data, avoiding any need for adversarial training, log-likelihood computation, or stochastic integration. This sample-driven design makes CFM an attractive alternative to diffusion and score-based methods—one that scales naturally to images, supports efficient training, and offers fine control over the geometry of the learned generative process.
In the following, we explore concrete and historically motivated choices for the mean \( \mu _t(x_1) \) and standard deviation \( \sigma _t(x_1) \). These special cases demonstrate how our general CFM framework can replicate or extend existing methods in generative modeling.
- Diffusion Conditional Vector Fields: By choosing \( \mu _t(x_1) \) and \( \sigma _t(x_1) \) to match the forward processes of classic diffusion models, we recover the conditional probability paths underlying popular score-based generative models. The resulting velocity fields coincide with the deterministic flows studied in probability flow ODEs, but are here derived directly from the conditional Gaussian interpolation perspective.
- Optimal Transport Conditional Vector Fields: We also consider choices where the conditional flow \( \psi _t(x_0) \) matches the displacement interpolant from Optimal Transport theory. These yield paths where particles move in straight lines with constant speed, offering simple, linear dynamics that contrast with the curvature seen in diffusion flows.
These examples not only highlight the flexibility of the CFM framework, but also demonstrate that by directly designing the conditional path \( p_t(x \mid x_1) \), we gain control over the structure and complexity of the regression task faced by the model. This perspective frees us from relying on SDEs or score-matching formulations, and instead empowers us to specify the flow behavior through deterministic, analytically-defined ingredients.
Let us now examine these special cases in detail.
Enrichment 20.10.4: Choosing Conditional Paths - Diffusion vs OT
Choosing Conditional Paths – Diffusion vs OT
A central design choice in Conditional Flow Matching (CFM) is the specification of the conditional probability path \( p_t(x \mid x_1) \) and its associated velocity field \( u_t(x \mid x_1) \). Since the framework imposes only minimal constraints—boundary conditions and mass conservation—we are free to define any smooth, valid interpolation from noise to data. Two prominent families of conditional flows have emerged:
- Diffusion-inspired paths, derived from time-reversed stochastic processes, follow curvature-inducing velocity fields and have been widely used in score-based generative models.
- Optimal Transport (OT) paths, defined via displacement interpolation between Gaussians, yield straight-line trajectories with constant-direction vector fields.
In what follows, we compare these constructions side by side, analyzing their flow geometry, computational implications, and suitability for CFM training. While diffusion paths align with existing literature and offer closed-form expressions under strong assumptions, we ultimately adopt the OT-based path due to its simplicity, numerical stability, and intuitive alignment with direct mass transport.
Variance Exploding (VE) Conditional Paths In the VE family of score-based models, the forward diffusion process begins at a data sample \( x_1 \) and progressively adds Gaussian noise until the distribution becomes nearly isotropic. Inverting this process defines a conditional flow that transforms noise into data.
For Flow Matching, the reversed VE schedule defines: \[ \mu _t(x_1) = x_1, \qquad \sigma _t(x_1) = \sigma _{1 - t}, \] where \( \sigma _t \) is an increasing scalar function with \( \sigma _0 = 0 \) and \( \sigma _1 \gg 1 \). This yields the conditional Gaussian: \[ p_t(x \mid x_1) = \mathcal {N}(x \mid x_1, \sigma _{1 - t}^2 I). \]
Applying Theorem 3 to this path, we obtain the conditional velocity field: \[ u_t(x \mid x_1) = - \frac {\sigma _{1 - t}'}{\sigma _{1 - t}} (x - x_1). \] This field points toward the target \( x_1 \), accelerating as \( t \to 1 \).
Variance Preserving (VP) Conditional Paths In the VP family, the diffusion process is defined to preserve total variance while gradually corrupting signal with noise. In reverse, this defines a tractable flow that interpolates toward data at a controlled rate.
Let: \[ \alpha _t = \exp \left ( -\frac {1}{2} \int _0^t \beta (s) \, ds \right ), \qquad T(t) = \int _0^t \beta (s) \, ds, \] where \( \beta (t) \geq 0 \) is a noise schedule. Then define: \[ \mu _t(x_1) = \alpha _{1 - t} x_1, \qquad \sigma _t(x_1) = \sqrt {1 - \alpha _{1 - t}^2}. \] This produces the conditional path: \[ p_t(x \mid x_1) = \mathcal {N}(x \mid \alpha _{1 - t} x_1, (1 - \alpha _{1 - t}^2) I). \]
From Theorem 3, the corresponding vector field is: \[ u_t(x \mid x_1) = \frac {\alpha _{1 - t}'}{1 - \alpha _{1 - t}^2} \left ( \alpha _{1 - t} x_1 - x \right ). \] This field decays more gradually than VE, producing smoother trajectories that reduce the risk of numerical instability near \( t = 1 \).
Limitations of Diffusion-Based Conditional Paths Despite being valid under Flow Matching, diffusion-based paths have several drawbacks:
- Non-convergent endpoints: Since \( \sigma _t \to 0 \) or \( \sigma _t \to \infty \) only asymptotically, the true boundary distribution \( p_0(x) = \mathcal {N}(0, I) \) is not reached in finite time.
- Nonlinear trajectories: The vector fields \( u_t(x \mid x_1) \) vary in both magnitude and direction over time, producing curved trajectories that are harder to approximate with a neural predictor.
- Overshooting and backtracking: Empirically, diffusion paths can overshoot the target before reversing course, wasting computation and requiring complex scheduling to stabilize.
These limitations motivate alternative constructions, such as the Optimal Transport conditional paths, which we explore next.
Optimal Transport Conditional Probability Paths
Flow Matching not only allows flexibility in choosing conditional paths—it also opens the door to highly principled constructions grounded in optimal transport (OT) theory. In this enrichment, we describe how the OT interpolation between Gaussians leads to an analytically simple and computationally superior conditional flow.
What Is Optimal Transport? Given two probability distributions \( p_0 \) and \( p_1 \), the Optimal Transport (OT) problem seeks the most efficient way to move mass from \( p_0 \) to \( p_1 \), minimizing a transportation cost. For quadratic cost, this defines the Wasserstein-2 distance: \[ W_2^2(p_0, p_1) = \inf _{\gamma \in \Gamma (p_0, p_1)} \int \|x - y\|^2 \, d\gamma (x, y), \] where \( \Gamma (p_0, p_1) \) is the set of couplings with marginals \( p_0 \) and \( p_1 \).
McCann’s Theorem [419] shows that the displacement interpolation \[ \psi _t(x) = (1 - t) \cdot x + t \cdot \psi (x), \] with \( \psi \) the optimal transport map, defines a geodesic \( p_t = [\psi _t]_{\#} p_0 \) in Wasserstein space. That is, OT interpolates between \( p_0 \) and \( p_1 \) using straight-line trajectories in distribution space.
Affine OT Flow Between Gaussians In the CFM setting, we define each conditional path \( p_t(x \mid x_1) \) as a Gaussian: \[ p_t(x \mid x_1) = \mathcal {N}(x \mid \mu _t(x_1), \sigma _t^2 I), \] with linearly evolving parameters: \[ \mu _t(x_1) = t x_1, \qquad \sigma _t = 1 - (1 - \sigma _{\min }) t. \] These satisfy the required boundary conditions: \[ p_0(x \mid x_1) = \mathcal {N}(x \mid 0, I), \qquad p_1(x \mid x_1) = \mathcal {N}(x \mid x_1, \sigma _{\min }^2 I). \]
The OT Vector Field Applying Theorem 3 to this linear Gaussian path yields the closed-form conditional velocity field: \[ u_t(x \mid x_1) = \frac {x_1 - (1 - \sigma _{\min }) x}{1 - (1 - \sigma _{\min }) t}. \] This field points directly from the current sample \( x \) to the target \( x_1 \), scaled by a time-dependent factor. Crucially:
- Its direction remains constant throughout time.
- Only the magnitude changes, increasing as \( t \to 1 \).
- The flow is affine and invertible.
The Corresponding Flow Map and CFM Loss The conditional flow map is: \[ \psi _t(x_0) = \sigma _t x_0 + \mu _t(x_1) = (1 - (1 - \sigma _{\min }) t) x_0 + t x_1. \] Differentiating with respect to time: \[ \frac {d}{dt} \psi _t(x_0) = (1 - \sigma _{\min }) (x_1 - x_0). \] Plugging this into the CFM loss gives: \[ \mathcal {L}_{\mbox{CFM}}(\theta ) = \mathbb {E}_{x_1 \sim q, \, x_0 \sim p} \left \| v_\theta (t, \psi _t(x_0)) - (1 - \sigma _{\min })(x_1 - x_0) \right \|^2. \] This is a time-independent regression target with linearly interpolated samples and a constant vector direction per sample pair \( (x_0, x_1) \).
Vector Field Geometry: Diffusion vs. Optimal Transport We now compare the structure of two commonly used conditional velocity fields in Flow Matching:
- Diffusion-based: \[ u_t^{\mathrm {diff}}(x \mid x_1) = \frac {1}{1 - t}(x_1 - x) \] is state and time dependent. As \( x \) moves along the trajectory, the direction of \( x_1 - x \) changes dynamically, producing curved paths. Moreover, the vector norm explodes as \( t \to 1 \), introducing numerical stiffness and instability.
-
Optimal Transport (OT)-based: \[ u_t^{\mathrm {OT}}(x \mid x_1) = \frac {x_1 - (1 - \sigma _{\min }) x}{1 - (1 - \sigma _{\min }) t} \] is an affine vector field in \( x \). The associated flow map solves the ODE: \[ \frac {d}{dt} x_t = u_t^{\mathrm {OT}}(x_t \mid x_1). \] It is easy to verify that the solution has the form: \[ x_t = (1 - (1 - \sigma _{\min }) t)\, x_0 + t\, x_1, \] which is a convex combination of \( x_0 \) and \( x_1 \), perturbed slightly by \( \sigma _{\min } \).
Why is this a straight line? Because:
- The path \( x_t \) is a weighted average of two fixed endpoints \( x_0 \) and \( x_1 \).
- The coefficients are smooth functions of \( t \).
- The velocity field \( u_t(x \mid x_1) \) always points in the same direction — from the current position \( x_t \) toward a fixed linear target.
The derivative \( \frac {d}{dt} x_t \) remains colinear with \( x_1 - x_0 \) at every point in time. Therefore, \( x_t \) traces a line segment — a curve whose tangent vector has constant direction (though varying magnitude). If \( \sigma _{\min } = 0 \), the path reduces to: \[ x_t = (1 - t)\, x_0 + t\, x_1, \] which is exactly a straight-line interpolation with constant speed.
Thus, OT-based vector fields induce linear transport flows in space — each particle follows a straight ray from \( x_0 \) to \( x_1 \) at time-varying speed.
Why Optimal Transport Defines a Superior Learning Signal
- 1.
- Straight-line trajectories. Solving the ODE \[ \frac {d}{dt} x_t = u_t^{\mathrm {OT}}(x_t \mid x_1) \] yields a linear path: \[ x_t = (1 - (1 - \sigma _{\min }) t) x_0 + t x_1. \] This is a straight-line trajectory between source and target. In contrast, diffusion-based paths accelerate nonlinearly, especially near \( t = 1 \), due to the divergence of the vector field.
- 2.
- Consistent direction. The OT velocity field maintains a constant direction for each sample pair \( (x_0, x_1) \), regardless of time. This means the neural network only needs to regress a fixed direction vector rather than learn a time-varying field, making the training signal simpler and more sample-efficient.
- 3.
- Zero divergence. Since \( u_t^{\mathrm {OT}} \) is affine in \( x \), its divergence \( \nabla \cdot u_t \) is constant. This greatly simplifies the log-likelihood computation via the Liouville identity: \[ \frac {d}{dt} \log p_t(x_t) = - \nabla \cdot u_t(x_t). \]
- 4.
- Efficient ODE integration. The Lipschitz constant of \( u_t^{\mathrm {OT}} \) is small and independent of \( t \), while the diffusion vector field \( u_t^{\mathrm {diff}} \) behaves like \( \propto \frac {1}{1 - t} \). As a result, OT flows require fewer solver steps, lower memory, and yield more stable gradients.
OT-based Conditional Flow Matching Inference Once training has converged, the learned neural velocity field \( v_\theta (t, x) \) defines a time-dependent transport field capable of moving samples from the base distribution \( p_0 \) (typically \( \mathcal {N}(0, I) \)) to the learned model distribution \( p_1 \). At inference time, this field is treated as the right-hand side of an ODE, and sample generation reduces to solving the initial value problem from a random noise sample.
- Sample initial noise \( x_0 \sim \mathcal {N}(0, I) \)
- Solve the ODE: \[ \frac {d}{dt} x_t = v_\theta (t, x_t), \qquad x_0 = x_{t=0} \]
- Integrate from \( t = 0 \) to \( t = 1 \) using an ODE solver (e.g., midpoint or Runge–Kutta)
- Return final sample \( x_1 = x_{t=1} \sim p_1 \)
In the OT setting, the ground-truth velocity field has an affine structure: \[ u_t^{\mathrm {OT}}(x) = \frac {x_1 - (1 - \sigma _{\min }) x}{1 - (1 - \sigma _{\min }) t}, \] The model learns to approximate this transport field using only the base sample \( x_0 \). The resulting trajectories follow straight paths with consistent direction and smoothly varying magnitude. Consequently, the learned field \( v_\theta \) is smooth and low-curvature, allowing efficient integration with just 10–30 steps—dramatically fewer than diffusion models, which often require hundreds due to stiffness near \( t = 1 \).
Takeaway Flow Matching permits any conditional path and velocity field that satisfy the continuity equation and match the boundary conditions. The Optimal Transport-based construction yields:
- Linear, closed-form trajectories.
- Constant-direction velocity fields.
- Tractable divergence computation.
- Dramatically improved sample efficiency.
For these reasons, OT-based conditional flows are often preferred in practice and form the foundation of modern CFM implementations.
Enrichment 20.10.5: Implementation, Experiments, and Related Work
Implementation Details Practitioners interested in applying Conditional Flow Matching (CFM) to their own datasets can refer to the following codebases:
- Official Flow Matching:
https://github.com/facebookresearch/flow_matching
This repository provides a clean PyTorch implementation of both continuous and discrete Flow Matching objectives. It includes examples of defining conditional Gaussian flows and training vector fields using small NNs. - Conditional Flow Matching for High-Dimensional Data:
https://github.com/atong01/conditional-flow-matching
This implementation extends CFM to image datasets like CIFAR-10 and CelebA using U-Net architectures. It includes training scripts, loss computation, and sampling pipelines. Users can adapt this repository to train models on their own data by modifying the dataset loader and network configuration.
Both codebases use the same core principle: sampling \( (x_0, x_1) \sim \mathcal {N}(0, I) \times q(x) \), computing \( x = \psi _t(x_0 \mid x_1) \), and minimizing the supervised loss \[ \left \| v_\theta (t, x, x_1) - \frac {d}{dt} \psi _t(x_0 \mid x_1) \right \|^2. \] This enables scalable training without evaluating score functions or marginal densities.
Empirical Results: OT vs. Diffusion The original Flow Matching paper [364] shows that using OT-based conditional vector fields leads to smoother flows, earlier emergence of structure, and more efficient sampling.
Quantitative Benchmarks Below is a comparison of Flow Matching with other generative modeling objectives on benchmark datasets. FM with OT consistently achieves lower negative log-likelihood (NLL), lower Fréchet Inception Distance (FID), and fewer function evaluations (NFE), outperforming score-based methods and diffusion-trained models.
| Model | CIFAR-10 | ImageNet 32×32 | ImageNet 64×64 |
||||||
|---|---|---|---|---|---|---|---|---|---|
| NLL ↓ | FID ↓ | NFE ↓ | NLL ↓ | FID ↓ | NFE ↓ | NLL ↓ | FID ↓ | NFE ↓ | |
| DDPM [223] | 3.12 | 7.48 | 274 | 3.54 | 6.99 | 262 | 3.32 | 17.36 | 264 |
| Score Matching | 3.16 | 19.94 | 242 | 3.56 | 5.68 | 178 | 3.40 | 19.74 | 441 |
| ScoreFlow [583] | 3.09 | 20.78 | 428 | 3.55 | 14.14 | 195 | 3.36 | 24.95 | 601 |
| FM (Diffusion path) | 3.10 | 8.06 | 183 | 3.54 | 6.37 | 193 | 3.33 | 16.88 | 187 |
| FM (OT path) | 2.99 | 6.35 | 142 | 3.53 | 5.02 | 122 | 3.31 | 14.45 | 138 |
Additional Comparisons For high-resolution datasets such as ImageNet 128×128, FM with OT also outperforms GAN-based baselines in terms of sample quality and tractability:
Flow Matching (FM) connects to and builds upon several influential research directions in generative modeling:
- Score-Based Generative Models: Denoising Score Matching [647] and probability flow ODEs [583] estimate the score \( \nabla _x \log p_t(x) \), which can be computationally expensive and unstable. FM avoids this by directly training on velocity fields derived from known conditional probability paths.
- Continuous Normalizing Flows (CNFs) and Neural ODEs: CNFs [87, 185] require solving and differentiating through ODEs for training, using the instantaneous change-of-variables formula. Flow Matching replaces this with a regression loss on known vector fields, avoiding backpropagation through ODE solvers and enabling stable and simulation-free training.
- Vector Field Regression Methods: Approaches such as OT-Flow [621] and Sliced Wasserstein Flows [718] aim to model transport vector fields but often lack closed-form supervision. Conditional Flow Matching (CFM) generalizes these ideas with tractable Gaussian paths and principled supervision over known conditional fields.
In addition, many works build upon FM to create new SOTA results, and improve training and inference times. Key such works include:
- Discrete Flow Matching and Language Modeling: Extensions such as Discrete Flow Matching [168] adapt FM to continuous-time Markov chains over discrete state spaces, broadening its applicability to structured data and natural language tasks.
- Riemannian Flow Matching: Recent work [86] generalizes FM to curved manifolds (e.g., protein structures or 3D geometry) by designing flows on Riemannian spaces. Conditional paths are constructed via geodesics rather than affine maps, preserving geometric constraints and enabling applications in biophysics and robotics.
- Multisample Flow Matching: Minibatch OT approaches [486] leverage more efficient couplings between source and target samples, reducing variance and improving training stability. These works extend FM to practical, large-batch implementations for real-world datasets.
- Optimal Flow Matching: Recent methods [302] aim to learn straight trajectories in a single step, enhancing the efficiency of flow-based generative models.
- Consistency Flow Matching: By enforcing self-consistency in the velocity field, Consistency Flow Matching [724] defines straight flows starting from different times to the same endpoint, improving training efficiency and generation quality.
- Bellman Optimal Stepsize Straightening: The BOSS technique [448] introduces a dynamic programming algorithm to optimize stepsizes in flow-matching models, aiming for efficient image sampling under computational constraints.
Together, these developments position Flow Matching—and particularly its conditional formulation (CFM)—as a versatile and scalable foundation for continuous-time generative modeling. It unifies ideas from score-matching, optimal transport, and neural ODEs, while enabling extensions to discrete, structured, and geometric domains.
Outlook Flow Matching with OT-based conditional paths currently offers one of the most promising trade-offs between theoretical clarity, empirical stability, and computational efficiency. Its compositional design—built around analytically specified conditional paths and closed-form velocity fields—creates a powerful and flexible foundation for developing future generative models across a wide range of domains.
Like diffusion models, Flow Matching supports conditioning on structured information (e.g., labels, prompts, segmentation maps), making it a natural candidate for controlled synthesis tasks. However, its deterministic trajectories and simulation-free sampling open the door to faster, more interpretable alternatives to stochastic generation frameworks.
Having now completed our exploration of generative modeling—from diffusion models like DDPM and DDIM to alternative frameworks such as Flow Matching—we conclude this chapter with a broader perspective. The field continues to evolve rapidly, driven by innovations in training stability, controllability, and cross-modal integration. Flow Matching, with its deterministic paths and modular design, offers a promising foundation for future research. As you continue your journey, we encourage you to explore how the principles introduced here may extend to new architectures, modalities, or creative applications yet to be imagined.
Enrichment 20.11: Additional Pioneering Works in Generative AI
The success of diffusion models and flow-based generative techniques has catalyzed a shift from low-level sample generation toward structured, semantically aligned systems. Today’s frontier lies not just in generating images, but in doing so under rich forms of control—such as natural language prompts, user sketches, or structural guidance. These systems are built by combining three key ingredients: (1) pretrained perceptual encoders (e.g., CLIP [498], T5 [501]), (2) structured conditioning modalities (e.g., text, pose, segmentation maps), and (3) latent-space modeling to handle high-resolution synthesis efficiently.
We begin our exploration with GLIDE [450], one of the first works to integrate classifier-free guidance with diffusion models for text-to-image generation. GLIDE marks a turning point in generative AI—it demonstrated that diffusion models, when paired with learned embeddings and careful guidance, could outperform prior autoregressive methods such as DALL\(\cdot \)E [509] both in realism and controllability. Building on this, later models introduced latent diffusion [531], personalization (e.g., DreamBooth [537]), and fine-grained conditioning (e.g., ControlNet [773]), each extending the flexibility and applicability of the core generative pipeline.
Enrichment 20.11.1: GLIDE: Text-Guided Diffusion with Classifier-Free Guidance
GLIDE [450] marked a turning point in text-to-image generation by demonstrating that high-quality, controllable synthesis can be achieved using an end-to-end diffusion model conditioned directly on natural language. Unlike earlier approaches such as DALL·E [509], which was originally built upon VQ-VAE, and discretized images into token sequences and applied autoregressive modeling, GLIDE operates in continuous pixel space, leveraging the denoising diffusion paradigm.
A central innovation in GLIDE is its use of a frozen text encoder—specifically a transformer model trained separately—to inject semantic conditioning into the diffusion process. By guiding each denoising step with a textual embedding, the model learns to associate complex descriptions with spatial features, enabling coherent synthesis even for novel or compositional prompts. This not only enables image generation, but also empowers applications such as text-driven inpainting, sketch refinement, and iterative editing.
GLIDE also introduced the now-standard technique of classifier-free guidance (CFG), which provides a tunable trade-off between diversity and fidelity without requiring an external classifier. This innovation would prove critical in subsequent systems including DALL·E 2, Imagen, and Latent Diffusion Models.
We now examine the GLIDE architecture, inference strategies, and capabilities—illustrating how this model served as a blueprint for the modern diffusion stack.
Model Architecture and Conditioning Mechanism GLIDE is a denoising diffusion probabilistic model (DDPM) that synthesizes images by learning to reverse a stochastic forward process. In the forward process, a clean image \( x_0 \in \mathbb {R}^{H \times W \times 3} \) is gradually perturbed with Gaussian noise: \[ x_t = \sqrt {\bar {\alpha }_t} \, x_0 + \sqrt {1 - \bar {\alpha }_t} \, \epsilon , \qquad \epsilon \sim \mathcal {N}(0, I), \] where \( \bar {\alpha }_t \in (0,1] \) is the cumulative product of noise schedule coefficients, and \( x_t \) is the noisy image at timestep \( t \). The model learns to predict the additive noise \( \epsilon \) using a U-Net denoiser \( \epsilon _\theta (x_t, t, y) \), where \( y \) is a natural language prompt describing the image content.
To condition on \( y \), GLIDE uses a frozen Transformer-based text encoder that converts the prompt into a sequence of contextual token embeddings. These embeddings are fused into the U-Net through cross-attention modules inserted at multiple spatial resolutions. This design enables the image representation at each location to selectively attend to different textual components, enforcing semantic alignment between visual structure and linguistic content. Two encoder variants are considered in the paper: a Transformer trained from scratch on image–text pairs, and the CLIP text encoder [498].
The objective used during training is a conditional variant of the DDPM noise prediction loss: \[ \mathcal {L}_{\mbox{GLIDE}} = \mathbb {E}_{x_0, \epsilon , t} \left [ \left \| \epsilon - \epsilon _\theta (x_t, t, y) \right \|^2 \right ], \] where the model learns to denoise \( x_t \) using both temporal and semantic information. This conditional learning setup allows GLIDE to support tasks like text-to-image synthesis, inpainting, and semantic image editing with a unified architecture.
As seen in Figure 20.71, GLIDE generalizes beyond literal training examples, demonstrating strong compositional ability and visual realism. This is made possible by its tight fusion of image-space diffusion and language semantics via cross-attention, allowing for rich conditional control.
Text Conditioning via Cross-Attention in GLIDE
In GLIDE [450], natural language prompts are embedded using a frozen Transformer encoder, which maps the input caption \( y \) into a sequence of contextualized token embeddings: \[ y \longmapsto \left \{ \mathbf {e}_1, \dots , \mathbf {e}_L \right \}, \qquad \mathbf {e}_i \in \mathbb {R}^d. \] Each vector \( \mathbf {e}_i \) captures the meaning of a specific token (word or subword) in context—e.g., the vector for “dog” will be different in “a dog” versus “hot dog.” The full sequence \( \{ \mathbf {e}_i \} \) thus encodes the semantics of the entire caption.
To inject this textual information into the image generation process, GLIDE modifies the self-attention mechanism inside the U-Net with cross-attention, where visual features act as queries and the text embeddings as both keys and values. At each attention block, the model computes: \[ \mbox{Attn}(Q, K, V) = \mathrm {softmax} \left ( \frac {Q K^\top }{\sqrt {d}} \right ) V, \] where: \[ Q = W_Q f, \quad K = W_K e, \quad V = W_V e. \]
- \( f \in \mathbb {R}^{H \times W \times c} \): the current spatial feature map from the U-Net, flattened to shape \( (HW, c) \) and linearly projected to form queries \( Q \in \mathbb {R}^{HW \times d} \).
- \( e \in \mathbb {R}^{L \times d} \): the caption token embeddings (from the text encoder), projected to keys \( K \in \mathbb {R}^{L \times d} \) and values \( V \in \mathbb {R}^{L \times d} \).
Why this works:
- The query vector \( Q_i \) at each image location \( i \) specifies a directional probe: it ”asks” which text tokens are most semantically relevant to what the model is generating at that pixel or patch.
- The dot-product \( Q_i K_j^\top \) measures the alignment between image location \( i \) and text token \( j \). The softmax turns this into a probability distribution over tokens—effectively letting each image region focus on specific language concepts.
- The final attended feature is a weighted combination of the value vectors \( V_j \), which carry semantic context from the caption and allow the image generator to access and integrate that information.
This structure allows the model to learn that, for example, when the caption includes “a dog in a red hat,” the spatial regions depicting the hat should align with the embedding for “hat,” and the dog’s body with “dog.” No token is “highlighted” in isolation—instead, relevance emerges dynamically as a function of the image context via learned query-key similarity.
This cross-modal alignment is applied at multiple resolutions within the U-Net, ensuring that text guidance is accessible across coarse layouts and fine details. The conditioning is thus not a global label but a dynamic, token-wise modulation of image generation grounded in semantic correspondence between modalities.
GLIDE’s Multi-Stage Generation Pipeline: A Cascaded Diffusion Strategy
GLIDE [450] employs a cascaded diffusion approach to synthesize high-resolution images from text prompts. It holds a similar intuition to the one behind Cascaded Diffusion Models (CDMs) [225], that we’ve previously covered (Enrichment 20.9.4), only this time it is based on a text encoding and not a class encoding. GLIDE divides the generation task into multiple stages, each operating at a different spatial resolution. This staged architecture improves quality and efficiency by allowing each model to focus on a specific aspect of the generation process.
- Base diffusion model (64\(\times \)64): A text-conditioned DDPM generates low-resolution \( 64 \times 64 \) images from captions. It captures coarse global structure, composition, and semantic alignment with the prompt. Operating at a small scale allows for training on large and diverse datasets.
- Super-resolution model (64\(\to \)256): A second diffusion model performs resolution upsampling. It takes as input a bilinearly upsampled version of the base output and the same text embedding. Conditioned on both, it synthesizes a \( 256 \times 256 \) image with finer visual details while preserving the semantic intent.
- (Optional) Final upsampler (256\(\to \)512): An optional third-stage model further increases resolution and sharpness, generating high-fidelity \( 512 \times 512 \) images. This stage is particularly useful in domains requiring photorealism or precise detail.
Why use cascading? GLIDE’s design is consistent with the principles of cascaded diffusion:
- Modularity and separation of concerns: The base model handles semantic composition and spatial layout. Super-resolution stages specialize in refining texture, edges, and fine-grained detail. This decomposition simplifies the learning objective at each stage.
- Improved sample quality: Errors and ambiguities in early low-resolution predictions can be corrected at higher resolutions through guided refinement.
- Efficiency: Lower-resolution generation requires fewer parameters and less computation. Later stages can reuse a smaller amount of training data focused on resolution pairs.
Each stage is trained independently. The super-resolution models are trained on paired low- and high-resolution crops, conditioned on both the image and the shared frozen text encoder. This encoder ensures that semantic alignment with the prompt is preserved across all stages. Cross-attention is employed at multiple layers in the U-Net, aligning image regions with relevant textual concepts.
Super-Resolution Modules in GLIDE After producing a coarse sketch using the \( 64 \times 64 \) base model, GLIDE [450] refines the image through a sequence of independently trained super-resolution diffusion models, typically for the resolution upgrades \( 64 \!\to \! 256 \) and optionally \( 256 \!\to \! 512 \). Each stage is responsible for enhancing visual fidelity by introducing higher-frequency detail, guided by both the upsampled coarse image and the original text prompt.
Each super-resolution module follows a structured training process:
- The input is a low-resolution image \( x^{\mbox{low}} \), obtained by downsampling a high-resolution training image \( x^{\mbox{high}} \) from the dataset.
- This \( x^{\mbox{low}} \) is bilinearly upsampled to the target resolution (e.g., from \( 64 \!\to \! 256 \)).
- Gaussian noise is added to the upsampled image using the forward diffusion schedule for that resolution stage, yielding a noised version \( x_t \).
- The model is trained to denoise \( x_t \) toward the original high-resolution ground truth \( x^{\mbox{high}} \), conditioned on both the noisy image and the associated text prompt \( y \).
Crucially, the same image-caption pair \( (x^{\mbox{high}}, y) \) is used across all stages of the cascade:
- The base model learns to generate a \( 64 \times 64 \) approximation of \( x^{\mbox{high}} \) given \( y \).
- The first super-resolution model refines that to \( 256 \times 256 \), using the blurred/noised upsampled \( 64 \times 64 \) image and still supervising against the same \( x^{\mbox{high}} \).
- The second super-res model (optional) further refines toward \( 512 \times 512 \), again targeting the same \( x^{\mbox{high}} \), now upsampled and re-noised accordingly.
This architecture ensures that all models in the cascade are aligned on a common semantic and visual goal. While the inputs to each stage differ in resolution and noise level, the supervision target \( x^{\mbox{high}} \) and prompt \( y \) remain constant throughout. This coherence prevents semantic drift and enables precise refinement of the coarse image toward the intended final output.
All models share a frozen T5 encoder for text conditioning. The token embeddings \( \{ \vec {e}_1, \dots , \vec {e}_L \} \) produced by this encoder are injected via cross-attention at multiple U-Net layers, ensuring that every spatial region in the image remains grounded in the prompt throughout all diffusion steps.
By training each stage to recover the original high-resolution dataset image from progressively degraded inputs, GLIDE ensures that the final samples are not just upsampled blobs, but semantically faithful, high-fidelity images—each stage building upon and correcting the previous.
Relationship to Cascaded Diffusion Models (CDMs) GLIDE [450] and CDMs [225] both follow a multi-stage pipeline: a low-resolution base model generates coarse images that are progressively refined through super-resolution diffusion stages. While the overall architecture is similar, the two differ in how they encode conditioning and enforce robustness during upsampling.
-
Conditioning and Guidance:
- GLIDE is conditioned on natural language via a frozen T5 encoder and uses classifier-free guidance (CFG) at inference. During training, 10% of prompts are dropped, allowing the model to learn both conditional and unconditional denoising. CFG interpolates their predictions to enhance prompt alignment.
- CDMs are class-conditioned using learned label embeddings injected into all models. No classifier-based or classifier-free guidance is used—class identity is always provided directly to the network.
-
Robustness via Degraded Conditioning:
- Both models degrade the upsampled low-resolution image before denoising. GLIDE uses fixed methods such as Gaussian blur and BSR, whereas CDMs apply randomized degradations (e.g., blur, JPEG compression, noise) drawn from a corruption distribution. This conditioning augmentation is more formally defined in CDMs and proven essential through ablations.
Summary: GLIDE and CDMs both use resolution-specific diffusion stages. The key differences are GLIDE’s use of natural language prompts and classifier-free guidance, versus CDMs’ reliance on class labels and stronger, randomized conditioning augmentation to maintain sample fidelity without external guidance.
Full Generation Pipeline of GLIDE
- 1.
- Base Diffusion Model (\( 64 \times 64 \)): A text-conditioned U-Net is trained using noise prediction loss to generate low-resolution samples that reflect the coarse layout and semantic intent of the prompt.
- 2.
- First Super-Resolution Stage (\( 64 \!\to \! 256 \)): The base image is upsampled and then re-noised. A second diffusion model is trained to remove the noise, refining texture, geometry, and visual coherence.
- 3.
- Optional Final Upsampler (\( 256 \!\to \! 512 \)): A third model further improves fidelity, handling fine details and photorealistic rendering. This model is trained with similar supervision but may use deeper architecture or stronger regularization.
Each model in the pipeline operates independently. All are conditioned on the same frozen T5 embeddings to ensure semantic consistency. Cross-attention is applied at various U-Net layers, so spatial features in the image are explicitly guided by token-level prompt information.
ADM U-Net Architecture in GLIDE The architecture of GLIDE [450] is built upon the ADM U-Net backbone introduced by Dhariwal and Nichol [122]. This network serves as the core denoising model at each stage of the diffusion cascade. While its layout resembles the canonical U-Net (see enrichment §15.6 and Figure [fig]), the ADM version integrates time and text conditioning, residual connections, and attention mechanisms in a more structured and scalable way.
Overall Structure. The U-Net processes a noisy input image \( x_t \in \mathbb {R}^{3 \times H \times W} \), a diffusion timestep \( t \), and a text prompt \( y \). The network is divided into three main components:
- Encoder path (downsampling): Each spatial resolution level includes two residual blocks and, optionally, a self-attention module. Downsampling is performed via strided convolutions, and the number of channels doubles after each resolution drop (e.g., 192 \( \to \) 384 \( \to \) 768).
- Bottleneck: At the lowest spatial resolution (e.g., \( 8 \times 8 \)), the model uses two residual blocks and one self-attention layer. This is where global semantic context is most concentrated.
- Decoder path (upsampling): This path mirrors the encoder. Each upsampling level includes residual blocks and optional self-attention, followed by nearest-neighbor upsampling and a \( 3 \times 3 \) convolution. Skip connections from the encoder are concatenated or added to the decoder at each level to preserve fine-grained detail.
Timestep Conditioning. The scalar diffusion timestep \( t \in \{0, \dots , T\} \) is encoded into a high-dimensional vector via sinusoidal embeddings, similar to the Transformer [644].
This vector is passed through a learnable MLP and injected into each residual block via FiLM-style modulation: \[ \mathrm {GroupNorm}(h) \cdot \gamma (t) + \beta (t), \] where \( \gamma (t), \beta (t) \in \mathbb {R}^d \) are scale and shift vectors derived from the timestep embedding, and \( h \) is the normalized activation.
Text Conditioning via Cross-Attention. The text prompt \( y \) is encoded using a frozen T5 encoder, yielding contextualized token embeddings \( \{ \vec {e}_1, \dots , \vec {e}_L \} \), with \( \vec {e}_i \in \mathbb {R}^d \). These are injected into the network via cross-attention in all attention layers. Each attention block computes: \[ \mathrm {Attn}(Q, K, V) = \mathrm {softmax}\left ( \frac {Q K^\top }{\sqrt {d}} \right )V, \] where: \[ Q = W_Q f, \quad K = W_K e, \quad V = W_V e, \] and \( f \in \mathbb {R}^{H \times W \times c} \) is the image feature map at that layer. This mechanism allows each spatial location in the image to query relevant semantic concepts from the caption.
Implementation Highlights. Key components of GLIDE’s U-Net implementation (adapted from glide_text2im/unet.py) include:
- Residual Blocks: All convolutional layers are embedded in residual units with FiLM-style conditioning and GroupNorm. Timestep embeddings and global pooled text embeddings are both added before nonlinearity.
- Attention Layers: Multi-head attention modules are inserted at intermediate resolutions (e.g., \( 64 \times 64 \), \( 32 \times 32 \), \( 16 \times 16 \)), depending on the stage (base model or super-resolution).
- Resolution Schedule: The base model uses four resolution levels with channel multipliers \([1, 2, 4, 4]\). Each resolution contains two residual blocks and an optional attention block. The total number of attention heads and layer width increases with resolution depth.
- Skip Connections: As in traditional U-Nets, skip connections copy activations from encoder layers to their corresponding decoder layers, enhancing spatial fidelity and stability during training.
Final Output. The decoder outputs a tensor \( \hat {\epsilon }_\theta (x_t, t, y) \in \mathbb {R}^{3 \times H \times W} \), representing the predicted noise. This estimate is used in the reverse diffusion step to move from \( x_t \to x_{t-1} \), progressively denoising toward the final image.
Summary of the GLIDE System GLIDE implements an early form of cascaded diffusion generation with the following key elements. It employs a text-conditioned U-Net backbone trained to synthesize low-resolution semantic content. It uses cross-attention mechanisms to maintain semantic alignment between the prompt and evolving image features. It applies a hierarchical cascade of independently trained super-resolution modules to improve fidelity and texture. This design enables scalable, prompt-consistent generation of high-resolution images without requiring auxiliary classifiers, external guidance models, or re-ranking. GLIDE’s architecture thus laid the foundation for subsequent cascaded frameworks, while demonstrating strong generalization across a wide range of text prompts and visual concepts.
Text-Guided Editing and Inpainting Capabilities Beyond pure text-to-image generation, one of GLIDE’s key contributions is its ability to perform conditional editing and inpainting through partial noising and constrained denoising steps. By erasing selected regions of an image, injecting Gaussian noise, and conditioning on both the surrounding pixels and a new text prompt, the model plausibly fills in missing content that respects the original style and semantics.
As shown in Figure 20.72, GLIDE performs image inpainting by conditioning the generative process on both a masked image and a guiding text prompt. To enable this capability, the model is fine-tuned specifically for inpainting using a dataset of partially masked images. During training, the model receives images with random rectangular regions removed and learns to denoise these masked regions while keeping the unmasked content fixed.
At inference time, the masked region is initialized with noise and updated using the standard diffusion sampling loop, while the known pixels are clamped to their original values at each step. This partial denoising scheme ensures that the generated content blends smoothly with the unmasked surroundings and adheres to the text condition.
Compared to GAN-based inpainting—which often requires adversarial losses and may fail to maintain semantic or spatial coherence—GLIDE leverages the stability and flexibility of its probabilistic denoising framework. The iterative nature of diffusion helps preserve global structure and yields completions that are both context-aware and text-consistent. Techniques such as classifier-free guidance can be retained during inpainting to further improve alignment with the prompt.
This mechanism also enables iterative refinement, wherein users can repeatedly mask regions, update the text prompt, and reapply the model to incrementally build complex scenes.
These capabilities demonstrate that GLIDE functions not just as a generator but as a flexible and interactive system for creative image manipulation. Its strength lies in preserving spatial coherence, semantic relevance, and stylistic fidelity across multiple user-guided editing stages.
Sketch-Based Conditional Editing with SDEdit GLIDE’s diffusion-based formulation enables an additional editing mode: sketch-to-image synthesis. By combining partial image inputs with language prompts, users can guide the model using both structure and semantics. This is achieved using a variant of Score-Based Generative Modeling known as SDEdit [422], which allows starting from a partially structured input and denoising it toward a visually coherent result.
In this setup, a user provides a crude input sketch or image fragment, alongside a prompt describing the desired output. The sketch is partially noised using the forward diffusion process (e.g., for 50 steps), and then the model is used to denoise it conditioned on the prompt. This ensures that the final image aligns with both the provided sketch and the semantic intent of the text.
As illustrated in Figure 20.74, this hybrid mode yields outputs that respect the geometric intent of the sketch while capturing nuanced prompt attributes (e.g., color, material, object integration). Because using this technique in this setup builds directly on GLIDE’s denoising framework, it remains versatile and general-purpose—capable of tasks like edge-to-image rendering, stroke-based painting, and compositional sketching.
This functionality bridges the gap between hand-drawn control and natural language generation, offering a compelling example of multimodal guidance in diffusion systems.
Classifier-Free Guidance vs. CLIP Guidance GLIDE introduces two competing strategies for aligning image generation with a textual prompt: CLIP guidance and classifier-free guidance (CFG). While both aim to steer the sampling trajectory toward semantic fidelity, they differ significantly in implementation, stability, and perceptual outcomes.
CLIP guidance [498] optimizes the cosine similarity between image and text embeddings produced by a frozen CLIP model: \[ \max _x \; \cos \left ( f_{\mbox{CLIP}}(x), f_{\mbox{CLIP}}(y) \right ). \] This gradient-based alignment is applied across the diffusion trajectory, encouraging denoised latents \( x_t \) to resemble images that CLIP deems semantically close to the prompt \( y \). While conceptually direct, this approach has several drawbacks:
- Gradient mismatch: CLIP is trained on fully denoised, high-quality images, whereas diffusion models operate over progressively noised latents. Applying CLIP’s gradients to noisy intermediate states introduces distributional mismatch, often steering the denoising trajectory off-manifold and resulting in unstable generation.
- Adversarial artifacts: Because CLIP is used both to guide and to evaluate image quality, the generative model may exploit weaknesses in CLIP’s embedding space. Instead of faithfully representing the prompt, it may synthesize images that trick CLIP into assigning high similarity scores—despite the samples being visually implausible or semantically incoherent to humans. This adversarial overfitting is particularly severe at high guidance scales, where the generator over-optimizes for CLIP alignment and produces unnatural textures or distorted compositions that ”hack” the metric.
- Tuning sensitivity: Effective use of CLIP guidance requires delicate balancing of the gradient scale. Weak guidance may yield vague or off-target generations, while overly strong guidance often causes prompt overfitting, repetitive artifacts, or structural collapse—manifesting as over-sharpened or corrupted outputs.
To partially address these limitations, GLIDE also experimented with a noised CLIP variant trained on corrupted images. While this reduced mismatch at early timesteps, it did not eliminate instability or the reliance on external model supervision.
Classifier-free guidance (CFG) [224], by contrast, is fully embedded into the model’s training objective. During training, the model randomly receives either a full prompt \( y \) or an empty (null) prompt \( \varnothing \), enabling it to learn both conditional and unconditional behaviors. At inference, these predictions are interpolated to amplify prompt fidelity: \begin {equation} \epsilon _{\mbox{CFG}} = \epsilon _\theta (x_t, t, \varnothing ) + s \cdot \left ( \epsilon _\theta (x_t, t, y) - \epsilon _\theta (x_t, t, \varnothing ) \right ), \end {equation} where \( s \geq 1 \) is the guidance scale.
CFG is simple, robust, and model-native. It requires no additional networks or loss terms, introduces no adversarial gradient pathways, and scales gracefully across prompts and domains. Although guidance inevitably reduces output diversity, GLIDE shows that CFG manages the fidelity–diversity trade-off more favorably than CLIP guidance. While CLIP guidance aggressively sacrifices variation to maximize alignment scores, CFG maintains perceptual quality without mode collapse.
This superiority is reflected in human preference studies. GLIDE uses Elo scoring—a rating system adapted from competitive games like chess—to compare pairs of samples from different guidance methods. Each approach accumulates points based on relative preference in head-to-head matchups.
Takeaway: Classifier-free guidance is a foundational technique for modern diffusion-based image generation. It integrates directly with the model’s architecture, avoids adversarial gaming of external metrics, and produces samples that are consistently favored by human evaluators. Its success in GLIDE set the stage for adoption in subsequent systems like Stable Diffusion [531], Imagen [540], and Parti [742].
Failure Cases and Architectural Limitations Despite its strong generative capabilities, GLIDE exhibits clear limitations when tasked with abstract reasoning, rare object compositions, or spatially intricate prompts. Failure cases include implausible geometries (e.g., “a car with triangular wheels”), semantic mismatches (e.g., “a mouse hunting a lion”), and weak attribute binding. Figure 20.77 illustrates such inconsistencies in spatial relationships, object placement, and compositional coherence.
These challenges stem, in part, from GLIDE’s architectural design. The model operates directly in pixel space using a cascade of resolution-specific diffusion U-Nets, from a \(64 \times 64\) base model to higher-resolution super-resolution modules. While this cascade enables high-fidelity output, it incurs significant computational cost and can propagate or amplify local inconsistencies—especially when text conditioning is vague or underspecified.
Text conditioning in GLIDE is injected via frozen T5 embeddings applied through cross-attention at each U-Net layer. While effective for common prompts, this mechanism is static and may fail to capture fine-grained semantics, particularly in rare or compositional settings. Attempts to enhance conditioning using CLIP guidance led to brittle behavior: though CLIP gradients improved prompt alignment metrics, they also introduced adversarial artifacts and degraded visual plausibility [450]. Even a noise-aware CLIP variant, trained on noised latents, did not eliminate these issues.
In contrast, classifier-free guidance (CFG) [224] proved more robust, offering sharper, more coherent samples while maintaining a reasonable fidelity–diversity trade-off. Still, GLIDE’s monolithic design entangles semantic interpretation and pixel-level synthesis in a single forward trajectory, limiting the model’s controllability and generalization to atypical prompts.
These limitations motivated a shift in architecture. Rather than generating images directly from text in pixel space, DALL·E 2 (also known as unCLIP) proposes a modular framework that decouples semantic modeling from image generation. The design consists of:
- A pretrained CLIP encoder that embeds the text prompt into a dense latent space.
- A prior model—either autoregressive or diffusion-based—that maps the text to plausible CLIP image embeddings \( \vec {z}_i \).
- A diffusion decoder that generates the final image conditioned on \( \vec {z}_i \) (and optionally the original text).
This two-stage pipeline enables specialization: the prior operates in CLIP’s compact semantic space, improving prompt generalization and sample diversity, while the decoder focuses purely on photorealistic rendering.
Unlike GLIDE, guidance does not collapse diversity in unCLIP, since semantic information is already embedded in \( \vec {z}_i \) and remains fixed during decoding [508]. As we will see, this architectural decoupling resolves several of GLIDE’s bottlenecks and introduces new capabilities—such as zero-shot image editing and text-guided variations.
Before introducing DALL·E 2 in depth, we briefly revisit its predecessor—DALL·E 1 [509]—which pioneered large-scale text-to-image synthesis using discrete visual tokens and an autoregressive transformer. Although limited in resolution and editability, DALL·E 1 established key ideas—such as VQ-VAE bottlenecks and joint modeling of image and text tokens—that laid the groundwork for modern generative systems.
Enrichment 20.11.2: DALL·E 1: Discrete Tokens for Text-to-Image Generation
Motivation: Turning Images into Token Sequences for GPT-Style Modelling DALL\(\cdot \)E 1 [509] reframes text-to-image generation as conditional autoregressive sequence modeling. Inspired by the success of GPT-3 [58], which generates fluent text by predicting one token at a time, DALL\(\cdot \)E extends this idea to vision: if an image can be represented as a sequence of discrete tokens, then a transformer could learn to ”write” images one token at a time, conditioned on a caption.
Applying GPT-style architectures directly to pixels is infeasible for two key reasons:
- Memory constraints: A \( 256 \times 256 \) RGB image contains nearly 200,000 pixel values, far exceeding the context length supported by transformers with quadratic self-attention.
- Low-level fidelity bias: Pixel-wise likelihoods encourage matching short-range visual details but are poor at capturing global semantic structure aligned with a text prompt.
To address these issues, DALL\(\cdot \)E adopts a two-stage pipeline:
- 1.
- Stage A — Discrete Visual Tokenization (VQ-VAE).
A Vector-Quantized Variational Autoencoder (VQ-VAE) is trained to compress and reconstruct images. Specifically:- The encoder downsamples a \( 256 \times 256 \) RGB image into a \( 32 \times 32 \) latent grid.
- Each latent vector is replaced with the nearest of \( K = 8192 \) codebook entries, producing a discrete token map \( z \in \{1, \dots , K\}^{32 \times 32} \).
- The decoder reconstructs the image from these discrete codes using nearest-neighbor embeddings.
After training, both the encoder and decoder are frozen. They serve distinct roles:
- The encoder is used to tokenize training images into fixed-length sequences of visual indices.
- The decoder is used at inference time to reconstruct the final image from the predicted image tokens.
- 2.
- Stage B — Transformer-Based Sequence Modeling.
Once the image-token vocabulary is defined by the VQ-VAE, DALL\(\cdot \)E trains a decoder-only Transformer to model the conditional distribution over joint text–image token sequences. The training input is a single, flattened sequence: \[ \underbrace {\mbox{[BPE-encoded caption tokens]}}_{\mbox{text context}} \;\|\; \underbrace {\mbox{[VQ-VAE image tokens]}}_{\mbox{target to predict}}, \] where || denotes concatenation. The model autoregressively learns to predict the next token given all previous ones, using a standard maximum likelihood objective.At inference time, the generation process unfolds in three main steps:
- (a)
- The input caption is tokenized using Byte Pair Encoding (BPE).
- (b)
- The Transformer autoregressively generates a sequence of 1024 discrete image tokens—each corresponding to a \( 32 \times 32 \) position in the image grid.
- (c)
- These image tokens are passed to the frozen VQ-VAE decoder, which transforms them into a full \( 256 \times 256 \) RGB image.
This stage completes the pipeline: the Transformer acts as a powerful prior over visual token sequences, and the VQ-VAE decoder serves as the renderer that translates discrete tokens into pixel-level images. The reuse of pretrained components ensures modularity, while the tokenized format enables the Transformer to operate over images in exactly the same way it operates over language—token by token.
This design turns the image generation task into a symbolic language modeling problem. By discretizing images, DALL\(\cdot \)E enables the reuse of scaling laws, architectures, and optimization methods originally developed for large language models. The VQ-VAE bottleneck plays a critical role: it reduces the transformer’s sequence length by a factor of 192, enforces a visual vocabulary, and allows the image generator to focus on semantic structure rather than low-level pixel precision.
Why not use a Vision Transformer (ViT) instead of a VQ-VAE? At the time of DALL\(\cdot \)E 1’s development (early 2020), ViT-style self-supervised encoders (e.g., SimCLR, BYOL, MAE) were not yet mature enough to support discrete symbolic modeling.
Could a ViT-style encoder work today? Yes—modern systems like VQ-GAN [148], MAE [210], and DALL\(\cdot \)E 2 combine transformer or CLIP-style features with either residual quantization or diffusion decoders. Advances in scalable mixed-precision training and robust quantization make ViT-based latent spaces viable. Later parts in this book revisit these improved architectures.
In summary, DALL\(\cdot \)E 1’s symbolic bottleneck—powered by a convolutional VQ-VAE—offered a compact, expressive, and discrete latent space for training GPT-style transformers over images. While ViT-based alternatives have since become popular, the VQ-VAE’s combination of discrete representation, efficient decoding, and architectural maturity made it the most practical choice at the time.
How VQ-VAE Enables Discrete Tokenization The tokenizer in DALL·E 1 [509] is based on a vector-quantized variational autoencoder (VQ-VAE), which converts high-resolution images into grids of discrete latent tokens. Specifically, it maps each \( 256 \times 256 \) RGB image into a \( 32 \times 32 \) grid, where each element indexes one of \( K = 8192 \) codebook vectors. These indices serve as compact image tokens for downstream modeling.
Training the Discrete VAE in DALL\(\cdot \)E 1. The VQ-VAE tokenizer used in DALL\(\cdot \)E 1 [509] maps high-resolution input images into a grid of discrete latent tokens, enabling downstream modeling with autoregressive transformers.
During training, the encoder processes the input image and outputs a spatial grid of logits \( \boldsymbol {\ell }_{i,j} \in \mathbb {R}^K \), where \( K \) is the number of codebook vectors and \( (i,j) \) indexes the spatial position in the latent map. These logits represent unnormalized log-probabilities over the discrete latent variables. A softmax is applied to yield a categorical distribution: \[ p_{i,j}(k) = \mbox{softmax}(\boldsymbol {\ell }_{i,j})_k, \] which defines the probability of selecting the \( k \)-th codebook vector at location \( (i,j) \).
Since sampling discrete indices is non-differentiable, the model applies the Gumbel-softmax relaxation [261] to enable end-to-end training. This technique approximates categorical sampling using a continuous, differentiable proxy. Instead of selecting a single index, the encoder produces a convex combination of the codebook vectors: \[ \vec {z}_{i,j} = \sum _{k=1}^K p_{i,j}(k) \cdot \vec {e}_k, \] where \( \vec {e}_k \in \mathbb {R}^d \) is the \( k \)-th learned codebook embedding. The resulting latent grid \( \{ \vec {z}_{i,j} \} \) is passed to the decoder, which attempts to reconstruct the original image.
The VQ-VAE in DALL\(\cdot \)E 1 is trained to maximize the Evidence Lower Bound (ELBO) on the log-likelihood of the data distribution. This objective consists of two terms:
-
Reconstruction loss: This term encourages the decoder to faithfully reconstruct the input image from its latent representation. During training, the decoder receives a softly quantized grid of latent vectors \( \vec {z} = \{ \vec {z}_{i,j} \} \), obtained via Gumbel-softmax relaxation over the encoder’s logits. The decoder outputs a reconstructed image \( \hat {x} = D_\theta (\vec {z}) \), which is compared to the original input \( x \).
The reconstruction loss assumes an isotropic Gaussian likelihood with unit variance at each pixel. This leads to a negative log-likelihood that simplifies to pixel-wise mean squared error (MSE): \[ \mathcal {L}_{\mbox{recon}} = \mathbb {E}_{x \sim \mathcal {D}} \left [ \left \| x - D_\theta (\vec {z}) \right \|_2^2 \right ]. \] Although MSE does not capture perceptual similarity (e.g., sensitivity to spatial misalignments or texture), it provides dense gradient feedback that encourages the encoder to preserve low-level spatial and textural details. These local features—edges, contours, and color regions—are crucial for producing discrete token sequences that retain semantic and structural information required by the downstream transformer.
More perceptually aligned metrics such as LPIPS [778] are often used in tasks that prioritize human visual judgment, but are computationally more intensive and less stable in early training. In contrast, MSE offers simplicity, efficiency, and sufficient structural fidelity for the purposes of compression and symbolic modeling.
-
KL divergence regularization: At each spatial location \( (i,j) \), the encoder outputs a categorical distribution \( p_{i,j}(k) \) over the \( K \) codebook entries. To discourage codebook collapse—a failure mode where only a small subset of the codebook is consistently used—the model includes a regularization term that penalizes deviation from a uniform prior: \[ \mathcal {L}_{\mbox{KL}} = \sum _{i,j} \mathrm {KL} \left [ p_{i,j}(k) \,\|\, \mathcal {U}(k) \right ], \] where \( \mathcal {U}(k) = \frac {1}{K} \) denotes the uniform categorical distribution over all \( K \) codebook entries.
This KL term encourages the encoder to distribute probability mass more evenly across the entire codebook. Without such regularization, the model may converge to using only a small number of tokens—those that are easiest for the decoder to reconstruct—thereby underutilizing the available representational capacity. This phenomenon, known as codebook collapse, reduces expressiveness and limits the diversity of visual patterns that the latent space can encode.
The uniform prior \( \mathcal {U}(k) \) reflects a modeling assumption that, across the dataset, all codebook entries should be equally likely. While this may not hold exactly in practice, it serves as a useful tool: by nudging the encoder’s output distributions \( p_{i,j}(k) \) closer to uniform, the model is encouraged to explore and specialize different code vectors. This improves latent diversity and makes the discrete token space more informative for downstream components such as autoregressive transformers.
The final objective function optimized during training is the ELBO: \[ \mathcal {L}_{\mbox{ELBO}} = \mathcal {L}_{\mbox{recon}} + \beta \cdot \mathcal {L}_{\mbox{KL}}, \] where \( \beta \) is a tunable hyperparameter that governs the trade-off between reconstruction fidelity and latent space regularization. A carefully chosen \( \beta \) ensures that the model learns discrete representations that are both structurally informative and uniformly distributed.
How is the codebook updated? Because the relaxed latent vector \( \vec {z}_{i,j} \) is a weighted average over the codebook entries, and the decoder is fully differentiable, the reconstruction loss induces gradients with respect to the codebook vectors \( \vec {e}_k \). These vectors are updated directly through backpropagation, with each one receiving a contribution proportional to its selection probability \( p_{i,j}(k) \) across spatial locations. This continuous relaxation allows efficient training of the discrete bottleneck.
Why is this relaxation valid if inference uses argmax?
At inference time, each spatial location \( (i,j) \) is assigned a discrete codebook index using a hard argmax over the encoder logits: \[ z_{i,j} = \arg \max _k \boldsymbol {\ell }_{i,j}[k]. \] This produces a symbolic grid of tokens that the transformer processes as a sequence over a fixed vocabulary. Since transformer models operate exclusively over discrete categorical inputs, these hard assignments are necessary for compatibility with downstream autoregressive generation.
However, during training, the non-differentiability of argmax prevents gradients from propagating into the encoder and codebook. To enable end-to-end optimization, the model instead uses a Gumbel-softmax relaxation [261]—a differentiable approximation to categorical sampling. For each location \( (i,j) \), the encoder outputs logits \( \boldsymbol {\ell }_{i,j} \in \mathbb {R}^K \), which are perturbed with Gumbel noise and scaled by a temperature \( \tau > 0 \) to yield soft categorical probabilities: \[ p_{i,j}(k) = \frac {\exp \left ((\boldsymbol {\ell }_{i,j}[k] + g_k)/\tau \right )}{\sum _{k'=1}^{K} \exp \left ((\boldsymbol {\ell }_{i,j}[k'] + g_{k'})/\tau \right )}, \qquad g_k \sim \mbox{Gumbel}(0, 1). \]
Here, the Gumbel noise \( g_k \) serves a specific purpose: it injects stochasticity that simulates sampling from a categorical distribution while keeping the operation differentiable. In effect, it perturbs the logits just enough to allow a continuous approximation of discrete sampling. The softmax over noisy logits mimics drawing from a categorical distribution in expectation, but permits gradients to flow through the output probabilities \( p_{i,j}(k) \). Without this noise, the relaxation would simply reduce to a softmax over logits and lose the stochastic behavior necessary to model discrete sampling during training.
The latent vector is then computed as a convex combination of codebook entries: \[ \vec {z}_{i,j} = \sum _{k=1}^{K} p_{i,j}(k) \cdot \vec {e}_k, \] where \( \vec {e}_k \in \mathbb {R}^d \) is the \( k \)-th learned codebook embedding.
The temperature \( \tau \) plays a central role in this process: it controls the sharpness of the softmax. At high values, the output distribution is diffuse, placing weight on multiple entries. As \( \tau \to 0 \), the distribution becomes increasingly concentrated on the largest logit, approaching a one-hot vector. To reconcile soft training with hard inference, \( \tau \) is gradually annealed during training—typically down to \( \tau = \tfrac {1}{16} \). This causes the encoder’s soft outputs to become sharply peaked, closely approximating the behavior of argmax by the end of training.
As a result, the decoder—trained on these increasingly sharp latent vectors—becomes robust to the true hard tokens it will encounter at test time. Meanwhile, a KL divergence term encourages the encoder to maintain high entropy across codebook usage, preventing mode collapse and promoting a rich, expressive latent space.
In summary, the Gumbel-softmax relaxation enables differentiable training by producing soft samples over codebook entries. The temperature parameter \( \tau \) controls how close these samples are to true one-hot vectors, while the Gumbel noise simulates discrete sampling in a smooth and trainable way. Together with annealing, reconstruction loss, and KL regularization, this mechanism allows the model to learn discrete latent codes that are both optimizable and fully compatible with transformer-based generation.
Note that while this simplification stabilizes training and integrates well with transformer-based generation, it comes at the cost of reduced discreteness. Each latent vector becomes a blend of multiple codebook entries rather than a single, clearly defined symbol. In contrast, models like VQ-VAE-2—though not designed to interface with transformers—use hard quantization to enforce strictly discrete representations. This is especially important in applications focused on compression, clustering, or symbolic reasoning, where each token must correspond to a well-defined and separable concept.
For instance, in tasks like class-conditional generation or latent space interpolation, soft assignments can blur distinct concepts (e.g., mixing “cat” and “dog” embeddings), leading to ambiguous representations. Hard assignments avoid this by ensuring each latent token corresponds to a single, interpretable codebook entry—even if training becomes more complex due to the non-differentiability of the quantization step.
Inference-Time Token Generation and Decoding
At inference time, DALL\(\cdot \)E 1 generates images directly from a text prompt—without any image input. The encoder of the VQ-VAE is bypassed entirely. Instead, the caption is first tokenized into a sequence of subword units using Byte Pair Encoding (BPE), which serves as context for a powerful decoder-only transformer. This transformer then autoregressively generates a sequence of 1024 discrete image tokens, each representing a codebook index in a \( 32 \times 32 \) spatial grid. Once the full token sequence is sampled, it is passed to the frozen VQ-VAE decoder to reconstruct a high-resolution \( 256 \times 256 \) RGB image.
- 1.
- The caption is tokenized into \( T_\mbox{text} \) BPE tokens: \( [x_1^{\mbox{text}}, \dots , x_{T_\mbox{text}}^{\mbox{text}}] \).
- 2.
- The transformer generates image tokens one by one: \[ x_{t}^{\mbox{image}} \sim p(x_t^{\mbox{image}} \mid x_1^{\mbox{text}}, \dots , x_{T_\mbox{text}}^{\mbox{text}}, x_1^{\mbox{image}}, \dots , x_{t-1}^{\mbox{image}}) \] for \( t = 1, \dots , 1024 \).
- 3.
- The resulting sequence is reshaped into a \( 32 \times 32 \) grid and decoded into pixels by the VQ-VAE decoder.
This architecture separates semantic generation from image rendering:
- The transformer serves as a semantic prior, generating a symbolic image consistent with the caption.
- The decoder acts as a neural renderer, translating discrete tokens into photorealistic pixel outputs.
Training the Transformer with Discrete Tokens
To enable text-to-image generation, the transformer is trained to model the joint distribution over text and image tokens: \[ p_\psi (\vec {x}^{\mbox{text}}, \vec {x}^{\mbox{image}}) = \prod _{t=1}^{T_\mbox{text} + 1024} p_\psi (x_t \mid x_1, \dots , x_{t-1}), \] where \( \vec {x}^{\mbox{text}} = [x_1^{\mbox{text}}, \dots , x_{T_\mbox{text}}^{\mbox{text}}] \) are the BPE-encoded caption tokens and \( \vec {x}^{\mbox{image}} = [x_1^{\mbox{image}}, \dots , x_{1024}^{\mbox{image}}] \) are the discrete image tokens derived from the VQ-VAE encoder via hard argmax quantization.
During training, these two sequences are concatenated into a single input: \[ [x_1^{\mbox{text}}, \dots , x_{T_\mbox{text}}^{\mbox{text}}, x_1^{\mbox{image}}, \dots , x_{1024}^{\mbox{image}}], \] and fed into the transformer, which is trained to predict each token in the sequence from its preceding context using a causal attention mask. The model performs next-token prediction across the entire sequence—first within the caption, then across the image region—with no distinction in architecture between the two parts.
Importantly, cross-modal conditioning arises naturally: since image tokens are positioned after the text tokens, they are allowed to attend to the entire caption. This enables the model to learn text-guided image synthesis within a unified autoregressive framework.
The loss function used is standard categorical cross-entropy over all tokens in the sequence: \[ \mathcal {L}_{\mbox{total}} = \sum _{t=1}^{T_\mbox{text}} \lambda _{\mbox{text}} \cdot \mathcal {L}_{\mbox{CE}}(x_t) + \sum _{t=T_\mbox{text}+1}^{T_\mbox{text}+1024} \lambda _{\mbox{image}} \cdot \mathcal {L}_{\mbox{CE}}(x_t), \] where \( \lambda _{\mbox{text}} \ll \lambda _{\mbox{image}} \) (typically \( \frac {1}{8} \) vs. \( \frac {7}{8} \)) to emphasize the importance of accurate image modeling. This bias reflects the downstream goal of generating images, not captions.
Additional regularization techniques—such as BPE dropout (which randomly alters token splits) and spatial attention priors over the image portion—are used to improve robustness and sample quality.
By training in this way, the transformer learns to interpret the caption as a prefix and generate a coherent visual token sequence conditioned on it. At inference time, the same structure is followed: given only a text prompt, the model samples tokens autoregressively to produce an image in the VQ-VAE’s discrete latent space.
Clarifying Terminology: dVAE vs. VQ-VAE The DALL\(\cdot \)E paper uses the term discrete VAE (dVAE) to refer to its tokenizer, which is effectively a VQ-VAE trained with soft relaxation. While VQ-VAE-2 [514] adds hierarchical levels and is suited to pixel-space autoregression, DALL\(\cdot \)E uses only a flat VQ-VAE and does not employ VQ-VAE-2 or hierarchical latent modeling.
Training Datasets and Sample Generation Pipeline DALL\(\cdot \)E 1 is trained on a large-scale dataset comprising 250 million (text, image) pairs scraped from the internet. Captions are tokenized using Byte Pair Encoding (BPE), while corresponding images are compressed into \( 32 \times 32 \) grids of discrete tokens via a VQ-VAE encoder. This diverse and weakly supervised corpus exposes the model to a broad spectrum of concepts and modalities, enhancing its generalization to novel text prompts at inference time.
During image generation, after receiving a text prompt, DALL\(\cdot \)E 1 begins the process of autoregressively sampling a sequence of 1024 discrete image tokens using a decoder-only sparse transformer with 12 billion parameters. Although the model’s weights are fixed and deterministic after training, the decoding process at inference time is deliberately stochastic.
At each of the 1024 generation steps, the model outputs a logit vector \( \boldsymbol {\ell } \in \mathbb {R}^{8192} \), corresponding to a categorical distribution over the image vocabulary. Instead of applying greedy decoding (selecting the most likely token at each step), the model samples from this distribution. To modulate the diversity of outputs, it uses temperature-based sampling, a method confirmed in the original paper [509]. The logits are rescaled as: \[ \tilde {p}_k \propto \exp \left ( \frac {\ell _k}{\tau } \right ), \] where \( \tau > 0 \) controls the sharpness of the softmax distribution. For \( \tau = 1 \), the model samples directly from the raw distribution; lower \( \tau \) values sharpen the probabilities (favoring high-confidence tokens), while higher values flatten them (increasing randomness). The authors report results under different temperatures, including \( \tau = 0.85 \) and \( \tau = 1.0 \), showing that trade-offs between diversity and fidelity can be tuned via this parameter.
It is important to note that even with a fixed temperature, the process remains non-deterministic. The temperature shapes the distribution but does not determine the sampled outcome. At each step, the model draws from a distribution with nonzero entropy—akin to rolling a die with unequal probabilities. Thus, for a fixed prompt and temperature, different sequences can still emerge due to randomness in token sampling.
To generate a batch of \( N \) candidate images, this entire sampling process is simply repeated \( N \) times. Each run yields a distinct sequence of 1024 discrete image tokens, reflecting a unique plausible interpretation of the same input caption. The diversity across these sequences arises entirely from stochastic sampling—there is no injected model-level noise (such as dropout) at generation time.
Once generated, each of the \( N \) sampled token sequences is decoded into a full-resolution \( 256 \times 256 \) RGB image using the pretrained and frozen VQ-VAE decoder. These images form the candidate pool for the subsequent CLIP-based reranking phase.
To select the most relevant images from the candidate set, DALL\(\cdot \)E applies a contrastive reranking strategy using CLIP [498], a pretrained model that embeds both text and images into a shared semantic space. Each image is scored by computing the cosine similarity between its embedding and the embedding of the input caption. The top-ranked images—those most semantically aligned with the prompt—are selected as final outputs.
This two-stage pipeline—stochastic sampling followed by CLIP-based semantic reranking—enables DALL\(\cdot \)E to generate high-quality and semantically faithful images from diverse prompts. During sampling, diversity is promoted through temperature-based decoding; during reranking, relevance is enforced by scoring candidates against the caption using CLIP [498]. This separation of concerns allows the model to handle ambiguous or open-ended prompts effectively: by increasing the number of samples \( N \), it becomes more likely that one or more generations will match the intent of the caption.
However, this strategy comes at a significant computational cost. Generating \( N = 512 \) high-resolution image candidates requires 512 full autoregressive decoding passes through a 12-billion parameter transformer and subsequent VQ-VAE decoding—making the approach expensive in both time and memory. While effective for research and offline applications, this procedure may be less practical in low-latency or resource-constrained settings.
Experimental Results and Motivation for DALL\(\cdot \)E 2 DALL\(\cdot \)E 1 delivers impressive zero-shot image generation capabilities, establishing a strong baseline for symbolic text-to-image synthesis. On MS-COCO captions, its samples are consistently preferred by human raters over those from prior work (e.g., DF-GAN [608]). In a best-of-five vote, DALL\(\cdot \)E’s generations were judged more realistic 90% of the time and more semantically aligned with the caption 93.3% of the time. These results are particularly notable given that DALL\(\cdot \)E was evaluated in a zero-shot setting—without task-specific fine-tuning.
Quantitative benchmarks further validate these findings. On MS-COCO, DALL\(\cdot \)E achieves a Fréchet Inception Distance (FID) competitive with state-of-the-art models—within 2 points of the best prior approach—and outperforms all baselines when a mild Gaussian blur is applied to reduce decoder artifacts. Its Inception Score (IS) also improves under similar conditions. However, on more specialized datasets like CUB [651], DALL\(\cdot \)E’s performance drops sharply, with a nearly 40-point FID gap between it and task-specific models. This limitation is visually evident in the model’s CUB generations: while bird-like in appearance, they often lack anatomical consistency and fine-grained control.
To address these challenges, DALL\(\cdot \)E 1 employs a clever reranking mechanism using a pretrained contrastive image–text model (CLIP [498]). From a large pool of candidate generations sampled from the transformer, a subset is selected based on similarity to the input caption in CLIP’s joint embedding space. As shown in Figure 20.81, increasing the number of samples from which to rerank (e.g., from 64 to 512) yields clear improvements in FID and IS, showcasing the power of contrastive alignment as a decoding prior.
Despite its pioneering design, DALL\(\cdot \)E 1 reveals key bottlenecks that limit generation quality: a fixed-length symbolic latent space, limited spatial resolution, and reliance on an autoregressive transformer prone to compounding errors. Moreover, its VQ-VAE decoder constrains the expressiveness of fine details and textures, and contrastive reranking—while effective—adds inference-time complexity.
These limitations laid the foundation for a more powerful successor. DALL\(\cdot \)E 2 abandons discrete tokenization in favor of CLIP-guided diffusion priors and cascaded super-resolution modules, enabling photorealistic outputs, improved compositionality, and open-vocabulary generalization. The next section explores this evolution in depth.
Enrichment 20.11.3: DALL\(\cdot \)E 2: Diffusion Priors over CLIP Embeddings
System Overview and Architectural Shift DALL\(\cdot \)E 2 [508] departs from the discrete-token autoregressive modeling of its predecessor by adopting a continuous latent diffusion framework grounded in the semantics of natural language and vision. Instead of generating symbolic image tokens (as in VQ-VAE + Transformer), DALL\(\cdot \)E 2 generates continuous CLIP image embeddings and decodes them into pixels using diffusion. This shift introduces greater flexibility, semantic expressiveness, and compositional fluency.
The full text-to-image generation pipeline comprises three major components:
- A frozen CLIP model [498], which embeds both text and images into a shared latent space via contrastive learning. In this space, semantic similarity corresponds to vector proximity—images and captions referring to the same concept are mapped close together. However, CLIP is not generative: it provides a static embedding space but cannot sample new embeddings or synthesize images.
-
A diffusion prior, trained to generate a CLIP image embedding from a given text embedding. Although text and image embeddings coexist in the same CLIP space, they are not interchangeable. Text embeddings primarily encode abstract, high-level semantic intent—what the image should conceptually depict—while image embeddings capture concrete, fine-grained visual details necessary for rendering a realistic image. Critically, only a subset of the embedding space corresponds to actual, decodable images: this subset forms a complex manifold shaped by natural image statistics.
To bridge the gap between abstract language and rich visual detail, the diffusion prior learns to sample from the conditional distribution over image embeddings given a text embedding. Instead of performing a deterministic projection (which might land off-manifold), it gradually denoises a sample toward the manifold of valid image embeddings, guided by the semantic signal from the text. This process ensures that the generated embedding is:
- 1.
- Semantically aligned with the input caption—anchored by the shared CLIP space,
- 2.
- Plausibly decodable into a coherent, photorealistic image—i.e., close to regions populated by real image embeddings.
The diffusion formulation also allows for stochasticity, making it possible to draw diverse but valid image embeddings from the same text input—capturing the one-to-many relationship between language and vision. For instance, the caption “a cat on a windowsill” might yield images with different lighting, poses, styles, or backgrounds—all plausible and semantically correct, but visually distinct.
-
A diffusion decoder, trained to reconstruct a high-resolution image from a CLIP image embedding. This decoder is based on the GLIDE architecture and operates directly in pixel space, not in a learned latent space as in traditional latent diffusion models (LDMs). It synthesizes images via a denoising diffusion process that is conditioned on the sampled CLIP image embedding. To further enhance semantic fidelity, the decoder can also incorporate the original CLIP text embedding as auxiliary context, enabling techniques such as classifier-free guidance—where conditioning signals are dropped stochastically during training and later reintroduced at inference to steer generation more precisely.
To produce high-resolution images, DALL·E 2 employs a cascade of diffusion models: a base model first generates a low-resolution \( 64 \times 64 \) image, which is then successively refined by two separate diffusion upsamplers—each responsible for enhancing resolution (e.g., to \( 256 \times 256 \) and ultimately \( 1024 \times 1024 \)). This multi-stage pipeline allows coarse scene structure and global composition to be resolved early, with fine textures and details added progressively. The result is a photorealistic image that faithfully reflects the semantic intent of the input caption and preserves the structural coherence implied by the CLIP embedding.
This architecture separates high-level semantics from low-level synthesis: the CLIP text embedding anchors generation in linguistic meaning, while the diffusion prior produces a visually grounded CLIP image embedding that is both semantically aligned and statistically plausible. By modeling a distribution over such embeddings, the system captures the one-to-many nature of text-to-image mappings—allowing multiple visually distinct yet valid outputs for the same prompt. Importantly, it ensures that sampled image embeddings lie on the manifold of realistic images, enabling successful decoding by the diffusion decoder.
Diffusion Prior: Bridging Text and Image Embeddings The diffusion prior serves as a generative model that maps text embeddings to image embeddings—both produced by a frozen CLIP model [498]. This replaces the discrete-token autoregressive Transformer of DALL\(\cdot \)E 1 with a continuous, stochastic generative mechanism. Its primary role is to synthesize plausible image representations (in CLIP space) that semantically align with a given text prompt.
Training Objective The DALL\(\cdot \)E 2 prior models the conditional distribution \( p(z_i \mid z_t) \), where \( z_t \in \mathbb {R}^d \) is the CLIP text embedding derived from a caption \( y \), and \( z_i \in \mathbb {R}^d \) is the corresponding CLIP image embedding. This latent embedding \( z_i \) is not the image \( x \in \mathbb {R}^{H \times W \times 3} \), but a dense, semantic vector encoding the high-level content of the image. The role of the prior is to bridge language and vision by mapping \( z_t \) to a plausible, text-consistent image embedding \( z_i \).
As in standard DDPMs [223], a forward noising process progressively corrupts \( z_i \) over \( T \) timesteps: \[ z_i^{(t)} = \sqrt {\alpha _t} z_i + \sigma _t \boldsymbol {\epsilon }, \qquad \boldsymbol {\epsilon } \sim \mathcal {N}(0, \mathbf {I}), \] where \( z_i^{(t)} \) is the noisy latent at timestep \( t \), and the scalars \( \alpha _t, \sigma _t \) are defined by a cosine variance schedule [449]. The diffusion prior, modeled by a Transformer-based network \( f_\theta \), learns to recover \( z_i \) from \( z_i^{(t)} \), conditioned on \( z_t \) and timestep \( t \): \[ \mathcal {L}_{\mbox{prior}} = \mathbb {E}_{z_i, z_t, t} \left [ \left \| f_\theta (z_i^{(t)}, z_t, t) - z_i \right \|_2^2 \right ]. \]
Conditioning on text \( z_t \) and timestep \( t \): The diffusion prior \( f_\theta \) is a decoder-only Transformer that predicts the clean CLIP image embedding \( z_i \in \mathbb {R}^d \) from its noisy version \( z_i^{(t)} \), conditioned on the text prompt \( y \), the global CLIP text embedding \( z_t \in \mathbb {R}^d \), and the current diffusion timestep \( t \in \{1, \dots , T\} \). All components are embedded into a sequence of tokens, each of dimensionality \( d_{\mbox{model}} \), and processed jointly by the Transformer.
Input sequence construction: At every denoising step \( t \), the model receives a token sequence of length \( N + 2 \), where \( N \) is the number of caption sub-word tokens. The sequence is composed as follows:
- 1.
- CLIP text embedding token: The global CLIP text embedding \( z_t \in \mathbb {R}^{d_{\mbox{CLIP}}} \) is projected to the model’s internal dimension and prepended to the sequence.
- 2.
- Caption tokens: The raw text \( y \) is tokenized and embedded via a learned text encoder (separate from CLIP), yielding a sequence \( \texttt{Enc}(y) = [e_1, \dots , e_N] \in \mathbb {R}^{N \times d_{\mbox{model}}} \) that captures fine-grained linguistic details.
- 3.
- Noisy image token: The current noised image embedding \( z_i^{(t)} \in \mathbb {R}^{d_{\mbox{model}}} \) is appended as the final token in the sequence. This is both a conditioning signal and the slot from which the prediction is read.
A learned timestep embedding \( \gamma _t \in \mathbb {R}^{d_{\mbox{model}}} \) is added elementwise to each token in the sequence: \[ \texttt{Input}_t = \left [ \mbox{Proj}(z_t),\, e_1, \dots , e_N,\, z_i^{(t)} \right ] + \gamma _t + \mbox{PE}, \] where PE denotes positional embeddings. The Transformer attends over the entire sequence using standard self-attention layers.
Prediction mechanism: Unlike architectures that introduce a special [OUT] token, DALL\(\cdot \)E 2 reuses the position of the noisy image token to emit the prediction. That is, the model’s output at the final sequence position is interpreted as the predicted clean embedding: \[ \hat {z}_i = f_\theta (\texttt{Input}_t)_{N+2}. \] This vector is supervised using a mean squared error loss against the ground truth image embedding \( z_i \): \[ \mathcal {L}_{\mbox{prior}} = \mathbb {E}_{(z_i, z_t, y),\, t} \left [ \left \| \hat {z}_i - z_i \right \|_2^2 \right ]. \]
Intuition: This conditioning layout minimizes token overhead while enabling the model to integrate coarse semantic alignment (\( z_t \)), fine-grained linguistic context (\( \{e_k\} \)), temporal information (\( \gamma _t \)), and noisy visual evidence (\( z_i^{(t)} \)). By sharing the input and output slot for \( z_i^{(t)} \), the model tightly couples conditioning and generation, which empirically improves stability and sample quality in latent space. The model acts as a semantic denoiser, iteratively refining its belief over \( z_i \) in a manner consistent with both language and the manifold of realistic CLIP image embeddings.
Why predict \( z_i \) instead of noise \( \boldsymbol {\epsilon } \)? In standard DDPMs, models are often trained to predict the noise vector \( \boldsymbol {\epsilon } \) added to the data, rather than the clean data itself. However, DALL\(\cdot \)E 2 found that predicting the uncorrupted latent \( z_i \) directly yields better results in the CLIP space. This choice is empirically motivated.
Cosine Noise Schedule: The prior uses the improved cosine schedule [449], which spreads signal-to-noise ratio (SNR) more evenly across timesteps. This mitigates the sharp gradient imbalances found in linear schedules—where learning is dominated by either near-clean or near-noise states—and instead concentrates learning signal in mid-range latents, which are most ambiguous and informative.
Intuition: The prior functions as a semantic denoiser in CLIP space. At inference time, it starts from random Gaussian noise \( z_i^{(T)} \sim \mathcal {N}(0, \mathbf {I}) \), and iteratively transforms it into a coherent image embedding \( z_i^{(0)} \approx z_i \) via reverse diffusion steps. Each step is guided not by the noise offset, but by the model’s direct prediction of the destination \( z_i \), enabling more targeted and text-consistent updates. This ensures that the final image embedding is both decodable—i.e., maps to a natural image \( x \)—and semantically grounded in the input prompt \( y \).
Model Architecture Two alternative approaches were considered for modeling the conditional distribution \( p(z_i \mid z_t) \), where \( z_t \in \mathbb {R}^d \) is the CLIP text embedding of the caption \( y \), and \( z_i \in \mathbb {R}^d \) is the corresponding CLIP image embedding. Both approaches aim to generate latent image features aligned with the input caption, but differ substantially in modeling assumptions, architecture, and inference dynamics.
-
Transformer-based diffusion prior: This is the main method used in DALL\(\cdot \)E 2. It operates in latent space using a denoising diffusion process over CLIP image embeddings \( z_i \). At each timestep \( t \), the model is given a noisy latent \( z_i^{(t)} \), the global CLIP text embedding \( z_t \), and an embedded version of the timestep \( t \), and predicts the clean latent \( z_i \) directly.
Unlike UNet-based architectures used in pixel-space diffusion models such as DDPM [223] or GLIDE [450], the prior is implemented as a decoder-only Transformer. The inputs—caption tokens, CLIP embedding, timestep embedding, and noisy latent—form a compact sequence that is processed by self-attention layers, enabling flexible and global conditioning. This architecture naturally supports compositionality and long-range dependencies, which are more difficult to encode in convolutional models.
A key architectural departure from earlier DDPM-style models is the absence of pixel-level upsampling paths or spatial hierarchies; instead, the Transformer operates entirely in the flat CLIP embedding space. The model outputs the prediction from the same token slot that received the noisy image latent \( z_i^{(t)} \), avoiding the need for a dedicated output token and keeping conditioning tightly coupled with prediction.
- Autoregressive prior: As an alternative, the authors also experimented with an autoregressive model over compressed image embeddings. The embedding \( z_i \) is first reduced via PCA and quantized into a sequence of discrete tokens, which are then modeled using a Transformer decoder. This approach allows for non-iterative sampling, greatly reducing generation time. However, it was found to severely limit sample diversity and compositional robustness. It often failed to represent visually complex or semantically unusual prompts, such as “a snail made of harp strings,” and exhibited classic autoregressive weaknesses like mode collapse.
The diffusion-based prior was ultimately adopted due to its superior expressiveness, semantic grounding, and generalization capabilities. Its iterative nature enables it to sample from a rich, multimodal distribution over image embeddings—capturing the diversity of possible visual instantiations for a given text prompt. Importantly, this process ensures that sampled latents:
- Lie on the CLIP image manifold—i.e., they decode to realistic images.
- Align semantically with the caption embedding \( z_t \).
Comparison to previous diffusion works: The DALL\(\cdot \)E 2 prior shares conceptual lineage with diffusion models like “Diffusion Models Beat GANs” [122] and GLIDE [450], but with several notable distinctions:
- It operates entirely in a latent space (CLIP embeddings), rather than in pixel space.
- It uses a Transformer instead of a UNet, facilitating flexible conditioning on textual tokens and enabling better compositional generalization.
- The prediction target is the original embedding \( z_i \), not the noise \( \boldsymbol {\epsilon } \), a choice empirically found to improve convergence and alignment in semantic spaces.
Sampling efficiency: Although operating in CLIP latent space reduces the dimensionality of the generative process, diffusion models remain computationally intensive due to their iterative nature. Each sample requires \( T \) sequential denoising steps—commonly 1000 or more in traditional DDPMs [223]—which can severely limit inference speed.
To address this, DALL\(\cdot \)E 2 adopts the Analytic-DPM sampler [395], a high-order numerical solver designed to accelerate denoising without sacrificing quality. Unlike the original DDPM sampler, which performs fixed-step stochastic updates, Analytic-DPM approximates the reverse diffusion process as an ordinary differential equation (ODE) and solves it using techniques from numerical analysis. Specifically, it constructs closed-form approximations of the score function’s integral using high-order Runge–Kutta or multistep methods.
Intuition: Whereas classical DDPM sampling views denoising as a Markov chain with small, noisy steps, Analytic-DPM reinterprets it as a continuous trajectory through latent space and computes this path more efficiently. By leveraging smoothness in the learned score function and adapting step sizes accordingly, the sampler produces high-fidelity outputs using significantly fewer steps. In practice, this allows DALL\(\cdot \)E 2 to reduce sampling to just 64 steps—an order of magnitude faster than original DDPMs—while maintaining perceptual quality and semantic alignment.
Further acceleration is possible via progressive distillation [542], which trains a student model to mimic the multi-step sampling trajectory of a teacher using only a few steps. This method compresses multi-step DDIM-style inference into 4–8 steps, enabling near real-time generation without major loss in sample diversity or quality.
Future directions for improving the prior: DALL\(\cdot \)E 2’s latent diffusion prior leverages CLIP space to produce semantically aligned image embeddings. Still, there is room to improve its efficiency and controllability. One avenue is to enhance the text conditioning pathway, such as scaling the text encoder or introducing structured cross-attention. As shown in Imagen [540], boosting language understanding often yields greater perceptual gains than enlarging the generator.
In parallel, alternatives like Flow Matching [364] propose learning deterministic vector fields to transport samples from noise to target latents. Trained with optimal transport, this approach can shorten generative paths and accelerate sampling—making it a promising direction for future priors.
Together, these advances in conditioning and transport modeling inform newer architectures such as DALL\(\cdot \)E 3, which further optimize semantic grounding and inference speed.
Diffusion-Based Decoder Once a CLIP image embedding \( \vec {z}_i \in \mathbb {R}^d \) is sampled from the diffusion prior, it is transformed into a photorealistic image by a cascade of diffusion models. This stage replaces the discrete VQ-VAE decoder used in DALL\(\cdot \)E 1 with a hierarchy of class-conditional diffusion models trained to generate increasingly detailed images from the continuous latent \( \vec {z}_i \). The decoder consists of three main components:
- A base decoder, trained to generate a \( 64 \times 64 \) RGB image from Gaussian noise conditioned on \( \vec {z}_i \).
- A mid-level super-resolution model, which upsamples the \( 64 \times 64 \) output to \( 256 \times 256 \), conditioned on both \( \vec {z}_i \) and the lower-resolution image.
- A high-resolution super-resolution model, which refines the image from \( 256 \times 256 \) to \( 1024 \times 1024 \), again conditioned on both \( \vec {z}_i \) and the previous output.
Each module in the cascade is implemented as a U-Net [532], modified to support semantic conditioning via cross-attention. At multiple layers within the U-Net, the CLIP image embedding \( \vec {z}_i \in \mathbb {R}^d \) is first projected through a learned MLP to produce a conditioning vector. This vector is then broadcast and used as the key and value in Transformer-style cross-attention blocks, where the U-Net’s intermediate activations serve as queries. This mechanism enables the model to inject global semantic context into spatially localized features during each denoising step.
This architecture follows the conditional pathway introduced in GLIDE (see Enrichment Enrichment 20.10.5), where cross-attention is used to integrate text embeddings. However, DALL\(\cdot \)E 2 replaces textual input with the CLIP image embedding \( \vec {z}_i \), and applies this conditioning across a cascade of three independently trained diffusion models—each specialized for a different output resolution.
All diffusion modules are trained separately using the standard noise prediction objective from denoising diffusion probabilistic models (DDPMs). Given a clean training image \( \vec {x}_0 \sim p_{\mbox{data}} \), the forward process produces noisy versions \( \vec {x}_t \) at discrete timesteps \( t \in \{1, \dots , T\} \) using the variance-preserving formulation: \[ \vec {x}_t = \sqrt {\bar {\alpha }_t} \vec {x}_0 + \sqrt {1 - \bar {\alpha }_t} \boldsymbol {\epsilon }, \quad \boldsymbol {\epsilon } \sim \mathcal {N}(0, I), \] where \( \bar {\alpha }_t \) defines a precomputed noise schedule. Each model is trained to predict \( \boldsymbol {\epsilon } \) from \( \vec {x}_t \), conditioned on both \( t \) and the CLIP embedding \( \vec {z}_i \), using the following loss: \[ \mathcal {L}_{\mbox{decoder}} = \mathbb {E}_{\vec {x}_0, \vec {z}_i, t, \boldsymbol {\epsilon }} \left [ \lambda (t) \cdot \left \| \boldsymbol {\epsilon } - \boldsymbol {\epsilon }_\theta (\vec {x}_t, t, \vec {z}_i) \right \|_2^2 \right ], \] where \( \lambda (t) \) is a weighting function that emphasizes earlier timesteps, which are often more uncertain and semantically significant.
Each model in the cascade integrates the global semantic embedding \( \vec {z}_i \) using cross-attention blocks inserted at multiple resolutions within a U-Net backbone. This mechanism allows the decoder to preserve semantic alignment throughout the generation process—from coarse layout at \( 64 \times 64 \) to fine-grained detail at \( 1024 \times 1024 \).
To upscale intermediate outputs, each super-resolution model is conditioned on both the CLIP embedding \( \vec {z}_i \) and the image produced by the preceding stage. These inputs are concatenated channel-wise and injected into the U-Net’s input layers, enabling the model to combine high-level semantics with spatial structure. This design preserves detail continuity across scales and mitigates the risk of semantic drift.
The cascaded diffusion strategy offers several advantages: modular training at different resolutions, efficient capacity allocation, and improved fidelity without sacrificing alignment. This architecture departs from the discrete token decoder used in DALL\(\cdot \)E 1, embracing a continuous latent refinement path. It also anticipates later systems such as Imagen [540] and Stable Diffusion [531], which similarly leverage latent diffusion and hierarchical super-resolution.
Semantic Interpolation and Reconstruction in CLIP Latents One of the key advantages of using CLIP image embeddings as the intermediate representation is the ability to manipulate and interpolate between visual concepts in a semantically meaningful way. Since the decoder learns to map from this continuous space to photorealistic images, it inherits the smoothness and structure of the CLIP embedding space.
DALL\(\cdot \)E 2 supports reconstruction from any CLIP image embedding \( \vec {z}_i \). This capability is demonstrated in reconstructions from progressively truncated principal components of the CLIP embedding. As shown in the following figure, low-dimensional reconstructions preserve coarse layout and object categories, while higher-dimensional reconstructions recover finer details such as texture, shape, and pose.
In addition, the model enables semantic variations by perturbing the CLIP embedding \( \vec {z}_i \) before decoding. By sampling different noise seeds or slightly shifting \( \vec {z}_i \), the decoder generates alternate renderings that retain the core semantics while altering attributes like style, viewpoint, or background content. This property is shown in the below figure, where variations of a logo and painting preserve their essential content while modifying incidental details.
Beyond single-image variations, the decoder also supports interpolation between CLIP embeddings. Given two embeddings \( \vec {z}_i^{(1)} \) and \( \vec {z}_i^{(2)} \), one can linearly interpolate to create intermediate representations: \[ \vec {z}_i^{(\alpha )} = (1 - \alpha ) \cdot \vec {z}_i^{(1)} + \alpha \cdot \vec {z}_i^{(2)}, \quad \alpha \in [0, 1], \] and decode each \( \vec {z}_i^{(\alpha )} \) to obtain a smooth visual transition. The following figure illustrates this, showing how both content and style blend across the interpolation path.
Further, textual edits can be translated into image modifications using vector arithmetic in CLIP space. If \( \vec {t}_1 \) and \( \vec {t}_2 \) are CLIP text embeddings corresponding to prompts like “a photo of a red car” and “a photo of a blue car”, one can construct: \[ \vec {z}_i^{\mbox{edited}} = \vec {z}_i + \lambda \cdot (\vec {t}_2 - \vec {t}_1), \] to steer the image generation toward a modified concept. This enables controlled, attribute-specific image edits as demonstrated in the below figure.
These capabilities demonstrate that the decoder does more than map a fixed vector to a fixed image—it enables meaningful navigation and manipulation within a high-dimensional semantic space. This design aligns well with human interpretability, creative applications, and interactive editing, bridging the gap between language and vision in a continuous and expressive manner.
Robustness and Generalization of the Decoder A notable strength of the DALL\(\cdot \)E 2 decoder lies in its ability to produce semantically coherent images even when faced with ambiguous or adversarial prompts. This property emerges from the decoder’s dependence on the CLIP image embedding \( \vec {z}_i \), which encodes high-level semantic content rather than raw text features. Despite the decoder’s lack of direct access to the original caption, its generation process remains surprisingly resilient.
The following figure exemplifies this phenomenon using typographic attacks. These are specially crafted images that contain misleading text elements designed to confuse vision-language models. The figure shows how, even when CLIP’s text-image alignment score is nearly zero for the correct label (e.g., “Granny Smith apple”), the decoder nonetheless produces plausible images consistent with the intended semantics.
The decoder’s robustness stems partly from the structure of the CLIP latent space, which prioritizes high-level semantic attributes while discarding low-level noise [498]. By conditioning on global CLIP embeddings rather than raw pixels, the decoder inherits a degree of semantic abstraction and resilience. This acts as a form of latent filtering, enabling generalization across modest perturbations and preserving semantic coherence even under ambiguous or corrupted inputs.
However, the decoder also inherits CLIP’s limitations. Because CLIP is trained contrastively on noisy web-scale data, its latent space can reflect biases or fail in edge cases—such as typographic attacks [179] or adversarial prompts [800]. These vulnerabilities propagate directly into the decoder, which lacks any mechanism to question or correct the conditioning input. As a result, failures in CLIP—e.g., misinterpretation of text-image associations or overfitting to dominant visual styles—can manifest as incoherent or misleading generations.
These issues highlight the trade-offs of using frozen, independently trained encoders for generative tasks. While such encoders provide efficiency and stability, they limit adaptability: the decoder receives no gradient feedback about misaligned latents and cannot adjust its interpretation dynamically. Future directions may involve closer coupling between encoder and decoder—through joint training, adaptive conditioning, or feedback mechanisms—to improve robustness and mitigate failures under distributional shifts.
Dataset Construction and Semantic Pretraining The foundation of DALL\(\cdot \)E 2 lies in its use of the CLIP model [498], which defines a shared latent space for text and images. CLIP is pretrained on a massive, web-scale dataset comprising over 400 million image–caption pairs. This dataset—structurally similar to LAION [555]—is curated by crawling the internet for images with surrounding natural language descriptions, such as alt text or nearby HTML content.
Each image–text pair in the dataset is treated as a weakly supervised alignment between visual content and language. No manual annotation is performed; instead, the system relies on heuristics such as language filters, deduplication, and image-text consistency scores to ensure basic data quality. The resulting corpus exhibits high diversity in style, domain, and resolution, but also inherits noise, biases, and artifacts common to large-scale web data.
CLIP is trained using a symmetric contrastive loss (InfoNCE), in which paired text and image embeddings are pulled together in latent space, while unpaired examples are pushed apart. This strategy produces a semantic embedding space where proximity reflects conceptual similarity, enabling zero-shot recognition and flexible conditioning in downstream generative models.
Because DALL\(\cdot \)E 2 reuses this fixed latent space for both its prior and decoder, the properties of the CLIP dataset fundamentally shape the behavior of the generation pipeline. The abstract, high-level alignment captured by CLIP allows the model to generalize across prompts and visual styles—but also introduces inherited limitations, such as uneven category coverage, culturally specific associations, and susceptibility to adversarial captions [179, 800].
Future systems may benefit from cleaner or more targeted datasets, multi-modal filtering techniques, or joint training strategies that better align vision and language across diverse distributions. However, the scale and breadth of LAION-style corpora remain essential for achieving the wide generalization capabilities characteristic of models like DALL\(\cdot \)E 2.
Image Quality and Diversity: Qualitative and Quantitative Results DALL\(\cdot \)E 2 demonstrates a significant leap in both sample fidelity and diversity compared to earlier models such as DALL\(\cdot \)E 1 and GLIDE [450]. Its design leverages the semantic richness of the CLIP latent space and the spatial precision of cascaded diffusion decoders to generate high-resolution images that are both realistic and semantically aligned with input prompts.
To evaluate zero-shot generalization, the authors compare DALL\(\cdot \)E 2 with other models on MS-COCO prompts. As shown in the following figure, DALL\(\cdot \)E 2 consistently produces more photorealistic and diverse outputs, outperforming both DALL\(\cdot \)E 1 and GLIDE in terms of visual quality and semantic relevance.
Qualitatively, the model captures fine stylistic variations and compositional semantics, even for abstract or imaginative prompts. Quantitatively, the authors report strong performance on both FID and CLIP score metrics, indicating a favorable balance between visual realism and prompt conditioning. Importantly, the model achieves these results without explicit caption-to-image pairing during decoder training, relying solely on alignment via CLIP embeddings.
Together, these findings affirm that at the time of publication, DALL\(\cdot \)E 2 achieved a new state-of-the-art in text-to-image synthesis, combining high sample quality with broad generalization and stylistic diversity.
Design Limitations and Architectural Tradeoffs Despite its impressive performance, DALL\(\cdot \)E 2 [508] exposes critical limitations that motivate further innovation. Most notably, the system’s reliance on a frozen CLIP encoder [498] introduces a structural bottleneck: the decoder generates images not from text directly, but from a static image embedding \( \vec {z}_i \) inferred from the CLIP text embedding \( \vec {z}_t \). This detachment limits the model’s capacity to resolve ambiguities in prompts or adapt to subtle shifts in meaning, especially for underrepresented concepts.
Because CLIP is pretrained independently on noisy web-scale data, it inherits biases and semantic gaps that the decoder cannot overcome. This can lead to mismatches between the user’s intention and the generated image, particularly in edge cases or when precision is required. Moreover, the three-stage pipeline—comprising the frozen encoder, the diffusion prior, and the cascaded decoder—adds system complexity and introduces potential fragility in the interfaces between components.
While this modular design supports reuse and targeted improvement, it also leads to a fragmented learning objective: no component is trained end-to-end with the final pixel output in mind. As a result, the system may excel in global compositionality but struggle with local consistency, prompting interest in more unified alternatives.
Stepping Towards Latent Diffusion Models The architecture of DALL\(\cdot \)E 2 [508] introduced a modular pipeline in which a frozen CLIP model provides a shared semantic space for both text and image, a diffusion prior generates image embeddings from text, and a cascaded decoder reconstructs full-resolution images. While this design offers flexibility and component reuse, it enforces strict boundaries between modules: the decoder receives only static CLIP embeddings, and the pipeline precludes gradient flow from image outputs back to the text encoder or semantic space. As a result, DALL\(\cdot \)E 2 cannot adapt its conditioning representations to improve prompt alignment or compositional accuracy during training. These limitations constrain its ability to generate coherent visual outputs for complex or nuanced captions.
Around the same time, Latent Diffusion Models (LDMs) [531] emerged as a unified alternative to modular architectures like DALL\(\cdot \)E 2. Instead of relying on frozen semantic embeddings as generation targets, LDMs train a variational autoencoder (VAE) to compress high-resolution images \( \vec {x} \in \mathbb {R}^{H \times W \times 3} \) into a spatially structured latent space \( \vec {z} \in \mathbb {R}^{h \times w \times d} \). This latent representation preserves both semantic content and spatial locality while significantly reducing dimensionality, allowing diffusion to operate over \( p(\vec {z}) \) rather than \( p(\vec {x}) \).
This decoupling of image space and generation space yields several key advantages. By performing diffusion in a compressed latent domain—typically of size \( h \times w \times d \) with \( h, w \ll H, W \)—LDMs significantly reduce the dimensionality of the generative process. This reduces memory consumption and accelerates training and inference, since the denoising network operates over fewer spatial locations and lower-resolution feature maps. While the final output must still be decoded into a full-resolution image, working in latent space greatly reduces the number of operations performed during iterative sampling.
Equally important is the spatial structure of the latent representation. Unlike global vectors such as CLIP embeddings—which collapse all spatial variation into a single descriptor—LDMs retain two-dimensional topology in the latent tensor \( \vec {z} \in \mathbb {R}^{h \times w \times d} \). This means that different spatial positions in \( \vec {z} \) can correspond to different image regions, allowing localized control and making it possible to model object layout, interactions, and spatial dependencies directly within the generative process.
Conditioning in LDMs is typically handled by a frozen text encoder (e.g., CLIP or T5), but rather than being used as a generation target, its features are injected into the denoising U-Net via transformer-style cross-attention modules at multiple spatial resolutions. This allows the model to integrate textual guidance at each step of the generation process.
This architectural strategy yields several compositional advantages:
- Spatially grounded text control: Prompt components (e.g., “a red ball on the left, a blue cube on the right”) can influence corresponding spatial locations in \( \vec {z} \), allowing for position-aware generation.
- Support for complex scene structure: The model can synthesize multiple entities with varied poses, attributes, and spatial relationships, reflecting the structure and grammar of the input prompt.
- Incremental and localized alignment: Because conditioning is applied repeatedly throughout the U-Net, the model can iteratively refine alignment with the prompt during denoising—rather than relying on a single global embedding passed at the start.
While the VAE and diffusion model are commonly trained separately for modularity and ease of optimization, they can also be fine-tuned jointly. This allows the learned latent space to adapt more directly to the generation task, potentially improving sample coherence and prompt fidelity.
In summary, LDMs replace static, globally pooled embeddings with a spatially structured, semantically responsive framework—laying the foundation for a new generation of controllable and scalable generative models. Although not originally proposed as a corrective to DALL\(\cdot \)E 2, LDMs address many of its limitations, such as the reliance on fixed embeddings, lack of spatial awareness, and modular non-differentiability. Stable Diffusion, released in mid-2022, embodies this design philosophy, offering high-resolution, prompt-aligned generation through a fully open and extensible latent diffusion pipeline.
OpenAI’s DALL\(\cdot \)E 3, introduced subsequently, is widely believed to adopt similar principles—including latent diffusion and closer integration with large language models such as GPT-4—to improve prompt adherence and editing flexibility. However, due to the proprietary nature of its architecture and training methodology, we now focus on the open and reproducible advances of latent diffusion models, which provide a transparent and theoretically grounded foundation for modern text-to-image generation.
Enrichment 20.11.4: Latent Diffusion Models (LDMs)
Overview and Conceptual Shift Latent Diffusion Models (LDMs) [531] represent a key evolution in generative modeling by addressing the inefficiencies of pixel-space diffusion. Traditional diffusion models, while powerful, operate directly over high-dimensional image tensors \( \vec {x} \in \mathbb {R}^{H \times W \times 3} \), making both training and sampling computationally expensive—especially for high-resolution generation. LDMs resolve this by first learning a perceptual autoencoder that maps images to a compact, spatially-structured latent space \( \vec {z} \in \mathcal {Z} \). Instead of modeling raw pixels, the denoising diffusion process unfolds within this learned latent space, where semantics are preserved but uninformative low-level details are abstracted away.
This architectural shift yields several benefits. Operating in \( \mathcal {Z} \) drastically reduces memory and compute costs, enabling high-resolution synthesis on modest hardware. The latent space is trained to preserve visually meaningful structures, improving the efficiency of generation. Moreover, conditioning signals—such as text, class labels, or image layouts—can be integrated directly into the latent denoising process via cross-attention mechanisms, giving rise to controllable, modular, and semantically aligned generation. We begin by braking down the components and training stages of LDMs, highlighting their conceptual differences from earlier approaches like DALL\(\cdot \)E 2 and motivating their widespread adoption in modern generative pipelines.
Autoencoder Architecture and Training Objective Latent Diffusion Models (LDMs) [531] begin by compressing images into a spatially structured latent space \( \vec {z} \in \mathcal {Z} \subset \mathbb {R}^{H' \times W' \times C} \), where \( H', W' \ll H, W \). This compression is achieved using a continuous variational autoencoder (VAE), whose goal is to preserve semantic information while discarding perceptually redundant pixel-level detail. The resulting latent representation balances fidelity with efficiency, enabling tractable diffusion modeling at high resolutions.
The encoder \( \mathcal {E}_\phi \) consists of a deep convolutional residual network that progressively downsamples the input image and outputs per-location Gaussian parameters \( (\boldsymbol {\mu }, \log \boldsymbol {\sigma }^2) \). Latent codes are sampled using the reparameterization trick: \[ \vec {z} = \boldsymbol {\mu }(x) + \boldsymbol {\sigma }(x) \odot \boldsymbol {\epsilon }, \qquad \boldsymbol {\epsilon } \sim \mathcal {N}(0, \mathbf {I}), \] ensuring differentiability for stochastic latent sampling. The decoder \( \mathcal {D}_\theta \) mirrors this structure with transposed convolutions and residual upsampling blocks to reconstruct the image \( \hat {x} = \mathcal {D}_\theta (\vec {z}) \).
The training objective combines four complementary losses:
- Pixel-level reconstruction loss: Ensures basic structural and color fidelity between the input and reconstruction. Typically chosen as \( \ell _1 \) or \( \ell _2 \) loss: \[ \mathcal {L}_{\mbox{pixel}} = \| x - \hat {x} \|_1 \quad \mbox{or} \quad \| x - \hat {x} \|_2^2. \] While effective at preserving coarse structure, this term alone often leads to overly smooth or blurry outputs due to averaging across plausible reconstructions.
- Perceptual loss (LPIPS): Mitigates blurriness by comparing activations (extraxcted features) from a pretrained CNN acting as a feature extractor \( \phi \), such as VGG16, in its final layer or in multiple intermediate layers: \[ \mathcal {L}_{\mbox{percep}} = \| \phi (x) - \phi (\hat {x}) \|_2^2. \] This loss encourages the decoder to preserve semantic and texture-level features, such as object boundaries and surface consistency, beyond raw pixels.
- KL divergence: Encourages the encoder’s approximate posterior \( q(\vec {z} \mid \vec {x}) \) to remain close to a fixed Gaussian prior \( \mathcal {N}(0, \mathbf {I}) \), \[ \mathcal {L}_{\mbox{KL}} = D_{\mbox{KL}} \left ( q(\vec {z} \mid \vec {x}) \parallel \mathcal {N}(0, \mathbf {I}) \right ). \] This term imposes structure and compactness on the latent space \( \mathcal {Z} \), which is essential for stable sampling and meaningful interpolation. By aligning \( q(\vec {z} \mid \vec {x}) \) with an isotropic Gaussian, the model ensures that randomly sampled latents resemble those seen during training—preventing degenerate or out-of-distribution samples. Moreover, it facilitates smoother transitions across the latent manifold, which is critical for tasks like class interpolation, latent editing, and controllable generation.
- Adversarial loss (optional): Introduced to restore high-frequency details that perceptual losses may not fully capture. A PatchGAN-style discriminator \( D \) is trained to distinguish real versus reconstructed patches: \[ \mathcal {L}_D = -\log D(x) - \log (1 - D(\hat {x})), \qquad \mathcal {L}_{\mbox{adv}} = -\log D(\hat {x}). \] This setup improves realism by aligning reconstructions with the local statistics of natural images, especially for textures such as hair, fabric, and foliage.
The total loss combines these components with tunable weights: \[ \mathcal {L}_{\mbox{total}} = \lambda _1 \mathcal {L}_{\mbox{pixel}} + \lambda _2 \mathcal {L}_{\mbox{percep}} + \lambda _3 \mathcal {L}_{\mbox{KL}} + \lambda _4 \mathcal {L}_{\mbox{adv}}. \]
In contrast to VQ-VAE architectures that discretize latents using a finite codebook, LDMs adopt a continuous latent space, allowing gradients to flow smoothly through the encoder and decoder. This continuity facilitates stable optimization. Furthermore, unlike approaches such as DALL\(\cdot \)E 2 that rely on frozen, externally trained embeddings (e.g., CLIP), the latent space \( \mathcal {Z} \) in LDMs is learned directly from data and refined through perceptual and adversarial objectives. As a result, the representations are not only compact but also well-aligned with the generative process, improving synthesis quality and of greater adaptability to the training domain.
Autoencoder Architecture and Latent Normalization Latent Diffusion Models (LDMs) [531] begin by compressing high-resolution images \( x \in \mathbb {R}^{H \times W \times 3} \) into a spatially structured latent representation \( \vec {z} \in \mathbb {R}^{h \times w \times C} \), where \( h \ll H \), \( w \ll W \), and typically \( C = 4 \). This compression is performed by a perceptual autoencoder consisting of a convolutional encoder \( \mathcal {E}_\phi \) and decoder \( \mathcal {D}_\theta \), trained separately from the generative diffusion model.
Encoder and Decoder Design The encoder \( \mathcal {E}_\phi \) is built from residual convolutional blocks with stride-2 downsampling, group normalization, and a spatial self-attention layer near the bottleneck. Rather than directly outputting the latent \( \vec {z} \), the encoder predicts a distribution over latents by producing two tensors of shape \( \mathbb {R}^{h \times w \times C} \): the mean \( \boldsymbol {\mu } \) and the log-variance \( \log \boldsymbol {\sigma }^2 \). These are concatenated into a single tensor of shape \( \mathbb {R}^{h \times w \times 2C} \) and used to sample latents via the reparameterization trick:
\[ \vec {z} = \boldsymbol {\mu } + \boldsymbol {\sigma } \odot \boldsymbol {\epsilon }, \qquad \boldsymbol {\epsilon } \sim \mathcal {N}(0, \mathbf {I}). \]
The decoder \( \mathcal {D}_\theta \) mirrors the encoder’s structure using upsampling residual blocks and convolutions. The final output passes through a tanh activation to restrict pixel values to the range \( [-1, 1] \), ensuring alignment with the normalized image input domain and promoting numerical stability.
# From ldm/modules/autoencoder/modules.py
class AutoencoderKL(nn.Module):
def encode(self, x):
h = self.encoder(x) # Conv + ResBlock + Attention
moments = self.quant_conv(h) # Projects to (mu, logvar)
return moments
def decode(self, z):
z = self.post_quant_conv(z) # Linear 1x1 conv
x_hat = self.decoder(z) # Upsample + Conv stack
return torch.tanh(x_hat) # Outputs in [-1, 1]Latent Normalization for Diffusion Compatibility After training the autoencoder, the encoder \( \mathcal {E}_\phi \) maps images \( x \in \mathbb {R}^{H \times W \times 3} \) to continuous latent representations \( \vec {z} \in \mathbb {R}^{h \times w \times C} \) via reparameterized sampling. These latents, however, typically have a standard deviation significantly larger than 1 (e.g., \( \hat {\sigma }_{\vec {z}} \approx 5.49 \) on ImageNet \( 256 \times 256 \)), since the encoder has not been trained with any constraint to normalize the latent scale.
To ensure compatibility with the noise schedules and assumptions of the downstream diffusion model—specifically, that the initial inputs should lie within a distribution close to \( \mathcal {N}(0, \mathbf {I}) \)—the latents are globally normalized by a scalar factor \( \gamma \), defined as the reciprocal of their empirical standard deviation:
\[ \tilde {\vec {z}} = \gamma \cdot \vec {z}, \qquad \gamma = \frac {1}{\hat {\sigma }_{\vec {z}}}. \]
This normalization is applied after training the autoencoder but before training the diffusion model. It ensures that the scale of the latent representations matches the variance assumptions of the DDPM forward process, allowing the use of standard Gaussian-based noise schedules (e.g., cosine or linear beta schedules) without requiring architectural or hyperparameter adjustments.
For example, if the empirical standard deviation of \( \vec {z} \) is \( \hat {\sigma }_{\vec {z}} = 5.49 \), then \( \gamma \approx 0.18215 \). This calibrated latent distribution becomes the new data domain \( \mathcal {Z} \subset \mathbb {R}^{h \times w \times C} \) over which the denoising diffusion model is trained.
By aligning the latent distribution with the assumptions of the diffusion framework, this scaling step improves training stability and sample quality, while retaining the benefits of working in a compact and perceptually aligned representation space.
Denoising Diffusion in Latent Space Once the variational autoencoder has been trained and frozen, Latent Diffusion Models (LDMs) reformulate the generative process as a denoising task in the latent space \( \mathcal {Z} \subset \mathbb {R}^{h \times w \times C} \). Rather than modeling high-dimensional pixel distributions, a Denoising Diffusion Probabilistic Model (DDPM) [223] is trained to model the distribution of latents produced by the encoder \( \mathcal {E}_\phi (x) \). For background on diffusion model fundamentals, see 20.9.0.1.0.
Given a clean latent \( z_0 = \mathcal {E}_\phi (x) \), the forward process gradually corrupts it through a fixed Markov chain: \[ q(z_t \mid z_{t-1}) = \mathcal {N}(z_t ; \sqrt {1 - \beta _t} \, z_{t-1}, \beta _t \, \mathbf {I}), \qquad q(z_t \mid z_0) = \mathcal {N}\left (z_t ; \sqrt {\bar {\alpha }_t} \, z_0, (1 - \bar {\alpha }_t) \, \mathbf {I} \right ), \] where \( \bar {\alpha }_t = \prod _{s=1}^t (1 - \beta _s) \) accumulates the noise schedule.
The denoising network \( \epsilon _\theta \) is trained to predict the noise \( \epsilon \sim \mathcal {N}(0, \mathbf {I}) \) added to the latent at each step. The objective is a mean-squared error loss: \[ \mathcal {L}_{\mbox{denoise}} = \mathbb {E}_{z_0, \epsilon , t} \left [ \left \| \epsilon - \epsilon _\theta (z_t, t, \tau ) \right \|_2^2 \right ], \] where \( z_t = \sqrt {\bar {\alpha }_t} \, z_0 + \sqrt {1 - \bar {\alpha }_t} \, \epsilon \), and \( \tau \in \mathbb {R}^{N \times d} \) is a sequence of embedded caption tokens from a frozen CLIP text encoder.
Importantly, all operations take place in the compressed latent space. The output \( z_0 \) of the reverse diffusion process is never directly decoded from the text, but instead synthesized through iterative noise removal guided by linguistic context. Only after this denoised latent is produced does the VAE decoder \( \mathcal {D}_\theta \) reconstruct the final image—bridging the semantic alignment in latent space with rendering in pixel space.
We now examine the architecture of \( \epsilon _\theta \), which must reconcile temporal, spatial, and textual conditioning across the entire denoising trajectory.
Architecture of the Denoising U-Net In Latent Diffusion Models (LDMs) [531], the denoising network \( \epsilon _\theta \) is a modified U-Net that operates entirely within a learned latent space \( \vec {z}_t \in \mathbb {R}^{h \times w \times C} \), where spatial structure is preserved despite dimensionality reduction. This latent space is produced by a pre-trained VAE encoder \( \mathcal {E}_\phi \), which maps high-resolution images \( x \in \mathbb {R}^{H \times W \times 3} \) into compact latent representations. During inference, the VAE decoder \( \mathcal {D}_\theta \) reconstructs the final image from a denoised latent \( \vec {z}_0 \). Thus, generation is fully decoupled from rendering: the diffusion model performs structured denoising in latent space, and the VAE handles the final image synthesis.
- Residual blocks: Each resolution stage of the U-Net uses residual blocks composed of convolution, group normalization, and nonlinearity, with a skip path that adds the block’s input to its output. This improves gradient flow and stability across the network depth, while supporting effective feature reuse in the latent space.
- Skip connections: Encoder–decoder symmetry is preserved by lateral skip connections that pass early, high-resolution latent features to later decoding stages. These connections maintain fine-grained spatial information—such as object boundaries and texture—that may otherwise degrade through diffusion noise and downsampling.
- Self-attention layers: Near the bottleneck, self-attention modules allow each latent location to attend to the full latent map. This models long-range dependencies critical for spatial relations like “above,” “behind,” or “next to,” and enables coherent global structure during denoising.
- Timestep conditioning: At each denoising step \( t \), the model is informed of the expected noise level via sinusoidal embeddings \( \vec {e}_t \), projected through an MLP to a vector \( \vec {\gamma }_t \in \mathbb {R}^C \). This conditioning vector is broadcast and added to intermediate feature maps \( \vec {h} \in \mathbb {R}^{C \times h \times w} \) inside each residual block: \[ \vec {h}' = \vec {h} + \mbox{Proj}(\vec {\gamma }_t). \] This simple additive modulation allows the model to adapt its behavior across timesteps, progressively refining coarse structure into fine detail as \( t \to 0 \).
-
Cross-attention conditioning: Semantic control is introduced via transformer-style cross-attention blocks applied at multiple U-Net resolutions. Given a caption embedding \( \tau \in \mathbb {R}^{N \times d} \), obtained from a frozen CLIP text encoder, each spatial feature in the latent map \( \vec {z}_t \in \mathbb {R}^{h \times w \times C} \) is projected to a query vector. The tokens in \( \tau \) are projected into keys and values. Attention is computed as: \[ \mbox{Attention}(\vec {q}, \vec {K}, \vec {V}) = \mbox{softmax}\left (\frac {\vec {q} \cdot \vec {K}^\top }{\sqrt {d}}\right )\vec {V}. \] This enables each latent location to dynamically attend to the most relevant parts of the prompt. For instance, if the caption is “a red cube on the left and a blue sphere on the right,” left-side latents focus more on “red cube,” while right-side latents emphasize “blue sphere”.
The advantages of this formulation include:
- Spatial specificity: Token-level attention guides individual regions of the latent map, enabling localized control.
- Semantic compositionality: Different parts of the prompt influence different subregions of the latent, enabling compositional generation.
- Dynamic guidance: The prompt influences the denoising at every step, enabling consistent semantic alignment throughout the trajectory.
This contrasts with global CLIP embedding approaches used in DALL\(\cdot \)E 2, which apply the prompt as a static conditioning vector, losing fine spatial control. Here, cross-attention integrates linguistic semantics into spatial generation at every scale and timestep.
Note on latent–image alignment: One might worry that the denoised latent \( \vec {z}_0 \) produced by the diffusion model may not match the distribution of latents seen by the VAE decoder during training. However, the diffusion model is explicitly trained to reverse noise from latents \( \vec {z}_0 \sim \mathcal {E}_\phi (x) \). Its denoised outputs are thus learned to lie within the latent manifold that the decoder \( \mathcal {D}_\theta \) can reconstruct from. The VAE does not condition on the text; instead, semantic alignment is handled entirely in the latent space through cross-attention before decoding. This separation ensures high-quality, efficient, and semantically grounded image generation.
Enrichment 20.11.4.1: Decoder Fidelity Without Explicit Text Conditioning
A natural concern in Latent Diffusion Models (LDMs) [531] is that the VAE decoder \( \mathcal {D}_\theta \) is not conditioned on the caption at inference. The diffusion model generates a latent code \( \vec {z}_0 \in \mathcal {Z} \) based on text input, but the decoder reconstructs an image from \( \vec {z}_0 \) unconditionally. This raises the question:
Can prompt-specific details be lost if the decoder never sees the text?
Why It Still Works Although the decoder ignores the caption, it operates on latents that were explicitly shaped by a text-conditioned diffusion model. The prompt’s semantics—object types, positions, colors—are baked into \( \vec {z}_0 \). The decoder’s job is not to reason about the prompt, but to faithfully render its visual realization from the latent code.
This works because:
- The VAE is trained to reconstruct real images from latents produced by its encoder, ensuring good coverage over \( \mathcal {Z} \).
- The compression factor (e.g., 4x or 8x) is modest, preserving fine detail.
- The diffusion model is trained on the encoder’s latent distribution, so its outputs lie within the decoder’s domain.
Trade-offs and Alternatives While this design is efficient and modular, it assumes the latent code captures all prompt-relevant detail. This may falter with subtle prompts (e.g., “a sad astronaut” vs. “a smiling astronaut”) if distinctions are too fine for \( \vec {z}_0 \) to preserve.
To address this, other models extend conditioning beyond the latent stage:
- DALL\(\cdot \)E 2 (unCLIP) [508] uses a second-stage decoder conditioned on CLIP embeddings.
- GLIDE and Imagen apply prompt conditioning throughout a cascaded diffusion decoder.
These improve prompt alignment, especially for fine-grained attributes, but increase compute cost and architectural complexity.
Conclusion In LDMs, text guidance occurs entirely in latent space—but that’s usually sufficient: if the denoised latent \( \vec {z}_0 \) accurately reflects the caption, the decoder can render it without ever “reading” the prompt. While newer models extend semantic control to the pixel level, LDMs offer an elegant and effective trade-off between simplicity and fidelity.
Classifier-Free Guidance (CFG) To enhance semantic alignment during sampling, Latent Diffusion Models incorporate Classifier-Free Guidance (CFG) [224]. Rather than relying on external classifiers to guide generation, the model is trained with randomly dropped conditioning information, enabling it to interpolate between conditional and unconditional outputs at inference time. The final prediction is given by:
\[ \hat {\boldsymbol {\epsilon }}_{\mbox{CFG}} = (1 + \lambda ) \cdot \hat {\boldsymbol {\epsilon }}_\theta (\vec {z}_t, t, \tau ) - \lambda \cdot \hat {\boldsymbol {\epsilon }}_\theta (\vec {z}_t, t, \varnothing ), \]
where \( \vec {z}_t \) is the latent at timestep \( t \), \( \tau \) is the CLIP-based text embedding, and \( \lambda \in \mathbb {R}_+ \) is a guidance weight. This simple yet powerful mechanism allows the diffusion process to be steered toward text-conformant latents while balancing visual diversity. For a detailed derivation and architectural breakdown, see Section Enrichment 20.9.3.
Empirical Results and Ablations LDMs have been evaluated across a wide range of tasks—unconditional generation, text-to-image synthesis, inpainting, and style transfer.
The authors conduct extensive ablations to identify design choices that contribute most to performance. Key insights include:
- Compression factor matters: Mild compression ratios (e.g., \( h, w \approx H/8, W/8 \)) retain sufficient perceptual detail for high-quality synthesis, outperforming VQ-based methods with more aggressive bottlenecks.
- Text-conditional cross-attention is essential: Removing spatial cross-attention layers results in poor prompt alignment, confirming that token-level attention is critical for semantic fidelity.
- Guidance scale tuning is nontrivial: Higher CFG values increase prompt adherence but reduce diversity and realism. For text-to-image synthesis, guidance scales in the range \( \lambda \in [4, 7] \) are often optimal.
- Decoder quality sets an upper bound: Even perfect latent alignment cannot recover prompt-relevant visual details if the decoder fails to reconstruct fine structure. Thus, VAE capacity indirectly limits generation fidelity.
- Task-specific fine-tuning improves quality: Inpainting, depth conditioning, and style transfer models trained on tailored objectives yield noticeably sharper and more controllable outputs than generic text-to-image models.
Limitations and Transition to Newer Works Like Imagen Latent Diffusion Models (LDMs) achieve a compelling trade-off between semantic guidance and computational efficiency by shifting diffusion to a compressed latent space. However, two key architectural limitations motivate newer designs:
- 1.
- Frozen CLIP Text Encoder: LDMs rely on a fixed CLIP encoder (e.g., ViT-B/32) for text conditioning, which was pretrained for contrastive image–text alignment, not generation. As such, it cannot adapt its embeddings to better serve the generative model. This limits the handling of nuanced prompts, rare entities, or abstract relationships, and its relatively small size constrains linguistic expressivity compared to large language models like T5-XXL.
- 2.
- Unconditional VAE Decoder: The decoder \( \mathcal {D}_\theta \) reconstructs images from latent vectors \( \vec {z}_0 \) without access to the guiding text prompt. While the denoising U-Net integrates semantic content into the latent, the decoder performs unconditional reconstruction. This design assumes the latent fully captures all prompt-relevant details—an assumption that may falter in complex or fine-grained prompts.
To address these issues, Imagen [540] introduces two key innovations:
- Richer Language Understanding: Instead of CLIP, Imagen uses a large frozen language model (T5-XXL) to encode prompts. This yields semantically richer and more flexible embeddings, better aligned with generation needs—even without end-to-end finetuning.
- Pixel-Space Diffusion: Imagen avoids latent compression during generation, performing denoising directly in pixel space or using minimal downsampling. This preserves visual detail and semantic fidelity more reliably than VAE-based reconstruction.
These improvements come at a cost: Imagen demands significantly higher computational resources during training and inference, due to both its larger backbone and pixel-level denoising. As explored next, the field continues to navigate the trade-off between efficiency and expressivity—balancing lightweight modularity with prompt-faithful generation quality.
Enrichment 20.11.5: Imagen: Scaling Language Fidelity in Text2Img Models
Motivation and Context Latent Diffusion Models (LDMs) [531] showed that pushing diffusion into a compressed VAE space slashes compute while preserving visual quality. Yet their design leaves all text conditioning to the UNet denoiser, because the VAE decoder itself is unconditional. For complex, compositional prompts, that separation can introduce subtle mismatches between what the caption asks for and what the pixels finally depict.
Imagen [540] turns this observation on its head. Through a careful ablation study the authors argue that text fidelity is limited more by the language encoder than by the image decoder. Scaling the caption encoder (T5 [501]) from Base to XXL delivers larger alignment gains than adding channels or layers to the diffusion UNets.
What is new in Imagen? The system freezes a 4.6-B-parameter T5-XXL to embed the prompt, then feeds that embedding into a three-stage diffusion cascade that progressively upsamples 64→256→1024 px. This coarse-to-fine recipe is familiar, but three engineering insights make Imagen unusually faithful to the text:
- Bigger language encoder \(>\) bigger image decoder. Ablations show that scaling the text backbone (e.g. T5-Large \(\rightarrow \) T5-XXL, \( \approx 4.6 \) B parameters) yields much larger improvements in prompt–image alignment than enlarging the diffusion UNets. Richer linguistic representations, not extra pixel capacity, are the main bottleneck.
- Dynamic-threshold CFG. Imagen applies classifier-free guidance but clips each predicted image to the adaptive \(p\)-th percentile before the next denoising step. This dynamic thresholding lets the sampler use higher guidance weights for sharper, more on-prompt images without colour wash-out or blown highlights.
- DrawBench. The authors curate a 200-prompt suite covering objects, spatial relations, counting, style, and abstract descriptions. In pairwise human studies on DrawBench, Imagen is preferred over both DALL·E 2 and Parti1.
In what follows we examine Imagen from four complementary angles:
- 1.
- Text \(\rightarrow \) Latent Coupling. We detail how the frozen T5-XXL encoder feeds its 4 096-dimensional embeddings into every UNet block, and why this cross-attention scheme is decisive for tight prompt grounding.
- 2.
- Three-Stage Diffusion Cascade. We walk through the \(64 \!\to \! 256 \!\to \! 1024\)-pixel pipeline and explain the dynamic-threshold variant of classifier-free guidance that stabilises high guidance weights without introducing blow-outs.
- 3.
- Ablation Take-aways. Side-by-side experiments reveal that scaling the language encoder delivers larger alignment gains than scaling the image UNets, and that guidance tuning outweighs most architectural tweaks.
- 4.
- Implications for Later Work. We point out how Imagen’s design choices foreshadow prompt-editing methods such as Prompt-to-Prompt and other text-controlled diffusion advances.
Cascaded Diffusion Pipeline
Imagen generates high-resolution images from text using a three-stage cascaded diffusion pipeline. A base model first synthesizes a coarse \( 64 \times 64 \) image conditioned on a text embedding. Two subsequent super-resolution (SR) diffusion models then refine this output to \( 256 \times 256 \) and finally to \( 1024 \times 1024 \), each conditioned on both the original text and the lower-resolution image. Noise conditioning augmentation is applied during SR training to improve robustness. This stage-wise design progressively enhances fidelity and detail while maintaining strong semantic alignment with the prompt.
Classifier-Free Guidance and Dynamic Thresholding
As outlined in Section Enrichment 20.9.3, classifier-free guidance (CFG) improves text-image alignment by combining predictions from a conditional and an unconditional denoising model. In particular, given a noisy sample \( \vec {z}_t \) at timestep \( t \), the denoised prediction is adjusted as
\[ \hat {{x}}_0^{\,(\mbox{CFG})} = (1 + \lambda ) \, \hat {\epsilon }_\theta (\vec {z}_t, t, y) - \lambda \, \hat {\epsilon }_\theta (\vec {z}_t, t, \varnothing ), \]
where \( \lambda \geq 0 \) is the guidance weight. Larger \( \lambda \) values push samples closer to the conditional manifold, increasing semantic fidelity—but they also amplify sharp transitions, outliers, and pixel intensities. This may lead to unnatural results, especially in high-resolution stages like \( 1024 \times 1024 \).
Problem: Oversaturation from Large Guidance Without any correction, high CFG weights cause the predicted clean image \( \hat {{x}}_0 \) to exhibit pixel values far outside the dynamic range of natural images (e.g., \([-1, 1]\) in normalized space). This leads to:
- Oversaturated colors, especially in backgrounds or small object regions.
- Loss of contrast and detail due to hard clipping of extreme values.
- Reduced diversity across samples due to overly confident predictions.
Naïve Solution: Static Thresholding One straightforward way to ensure that the final image remains in the valid pixel range (e.g., \([-1, 1]\)) is to apply static thresholding—that is, clipping the predicted clean image \( \hat {x}_0 \) to lie within this range:
\[ \hat {x}_0^{\,(\mbox{clipped})} = \mbox{clip}(\hat {x}_0, -1, 1). \]
While simple, this solution can degrade image quality when applied at every denoising step. During the iterative reverse process, the model may temporarily predict pixel values outside the target range to represent subtle visual cues—such as specular highlights, sharp edges, or deep shadows. These out-of-range values often reflect meaningful structure that will eventually be pulled into range by the final denoising steps. If we aggressively clip at each step, we risk:
- Flattening high-contrast regions: Highlights or shadows may be prematurely truncated, reducing the image’s perceived depth and richness.
- Introducing artifacts: Hard cutoffs can produce unnatural boundaries or saturation plateaus, especially in smooth gradients or textured areas.
- Destroying predictive consistency: The model’s learned denoising trajectory may rely on temporarily overshooting the target range before converging. Clipping interferes with this path, leading to less coherent results.
Because of these issues, it is more effective to defer clipping until the final step of the denoising process—once \( \hat {x}_0 \) is fully predicted. However, even this final-step clipping can still be problematic if the distribution of predictions varies across samples. This limitation motivates more adaptive solutions such as dynamic thresholding, which adjusts the clipping range based on the specific prediction statistics of each sample.
Dynamic Thresholding: an Adaptive Alternative to Static Clipping Method. Dynamic thresholding [540] rescales each denoised prediction \( \hat {{x}}_0 \in \mathbb {R}^{H \times W \times 3} \) by a sample-specific scale before clipping to \([-1, 1]\). This scale \( s \) is set to the \( p \)-th percentile (typically \( p = 99.5 \)) of the absolute pixel magnitudes:
\[ s = \mbox{percentile}(|\hat {{x}}_0|,\; p), \quad \hat {{x}}_0^{\,(\mbox{dyn})} = \mbox{clip}\left ( \frac {\hat {{x}}_0}{s},\; -1,\, 1 \right ). \]
This adaptive rescaling ensures that only the top \( (100 - p)\% \) of pixel values—those with the most extreme magnitudes—are affected, while the bulk of the image retains its original brightness and contrast. By adapting the clipping threshold to each image individually, dynamic thresholding avoids global overcorrection and better preserves subtle visual detail.
Why it works (with examples and reasoning).
During denoising—especially under strong classifier-free guidance or at high resolutions—the model often predicts pixel values slightly outside the legal image range \([-1, 1]\). These excursions may encode meaningful high-frequency details (like glints, reflections, or fine textures), but they can also include spurious outliers (e.g., sharp halos, single-pixel spikes).
Static clipping flattens all values beyond this range, indiscriminately truncating both legitimate signal and noise. For example, if a predicted pixel value is \( \hat {x}_0 = 1.5 \) and the 99.5th percentile sets \( s = 1.4 \), then dynamic thresholding performs:
\[ \hat {x}_0 = 1.5 \longrightarrow \frac {1.5}{1.4} \approx 1.07 \longrightarrow \mbox{clipped to } 1.0, \quad \hat {x}_0 = 1.2 \longrightarrow \frac {1.2}{1.4} \approx 0.86 \quad \mbox{(preserved)}. \]
Here, even though both values exceed the legal range, only the more extreme outlier gets clipped. Crucially, rescaling does reduce the absolute intensity of all values, but it preserves their relative differences. The 1.2 pixel remains brighter than others around it, so its visual role as a highlight is maintained. This distinction would be erased by static clipping, which collapses all values above 1.0 into a hard ceiling.
Dynamic thresholding thus provides a soft-constraint mechanism that acts proportionally to the sample’s content:
- It preserves expressive range by maintaining contrast between midtones and peaks, avoiding the flattening effect of uniform truncation.
- It targets only extreme outliers—often isolated and perceptually disruptive—without globally lowering brightness or contrast.
- It protects sharp detail and texture, where small overshoots encode fine structure (like fur, edge reflections, or legible small text) rather than error.
By tailoring its response to each image’s intensity distribution, dynamic thresholding ensures semantic expressivity and local fidelity—especially important under aggressive guidance or when synthesizing high-resolution content.
Experimental Findings and DrawBench Evaluation
Scaling the Text Encoder A central insight of Imagen [540] is that text encoder quality is a dominant factor in text-to-image generation. In systematic ablations, the authors vary the underlying language model used to encode the caption—comparing T5-Base, T5-Large, T5-XL, and T5-XXL—and observe consistent improvements in both image-text alignment and visual fidelity as model size increases.
These results motivate a design shift: instead of primarily scaling the image generator (as done in prior works), Imagen prioritizes high-capacity language understanding, even when the encoder is frozen during training. This strengthens the mapping from prompt to semantic features, yielding more accurate and coherent visual generations.
DrawBench: A Diverse Prompt Evaluation Suite To evaluate generative performance beyond cherry-picked prompts, the authors introduce DrawBench, a human preference-based benchmark of 200 prompts spanning multiple semantic categories:
- Object and scene composition
- Spatial relationships and counting
- Style and texture
- Complex language grounding
Each model (e.g., Imagen, DALL\(\cdot \)E 2, GLIDE, LDM, VQGAN+CLIP) generates images for each prompt, which are then compared in a blind A/B format for:
- Alignment: Does the image accurately reflect the text prompt?
- Fidelity: Is the image visually plausible and high-quality?
Imagen significantly outperforms the baselines on both axes, demonstrating the effectiveness of its text encoder, CFG tuning, and cascading architecture.
Qualitative Samples Finally, the model produces diverse, photorealistic samples across various creative and grounded prompts:
Enrichment 20.11.5.1: Toward Fine-Grained Control and Editable Generation
From Fidelity to Controllability While models like Imagen [540] and DALL\(\cdot \)E 2 [508] have achieved remarkable success in photorealism and semantic alignment, they remain fundamentally non-interactive. Once an image is generated from a text prompt, the process is opaque: users have no control over which elements change if the prompt is revised.
This poses a major limitation in creative and iterative workflows. For example, a designer modifying the prompt from “a red car” to “a blue car” expects only the car’s color to change, while preserving the original composition, lighting, and style. In practice, however, standard diffusion pipelines—including those using classifier-free guidance (CFG)—often regenerate the image from scratch, with unpredictable changes to unrelated regions.
Why Prompt-Aware Attention Control Is Needed To address this, recent work focuses on editable generation—where models support localized updates, identity preservation, and deterministic user control. Three key goals underpin this new research direction:
- Fine-grained editability: Allow prompt-based modifications (e.g., changing “cat” to “dog”) without altering unrelated image regions.
- Semantic preservation: Maintain critical attributes such as object identity, layout, and lighting even after prompt edits.
- Interactive control: Introduce modular control signals—like segmentation masks, edge maps, or pose estimations—that act as “handles” for spatial or structural guidance.
Key Approaches and Innovations A growing ecosystem of techniques now forms the foundation for controllable diffusion-based generation—each offering distinct mechanisms for enabling user-guided synthesis:
- Prompt-to-Prompt (P2P) [217]: Introduces a novel method for prompt-driven editing by intervening in the model’s cross-attention maps during inference. Instead of retraining or re-encoding, it aligns attention weights across similar prompts to preserve spatial layout and object identity. This enables intuitive text modifications (e.g., “red shirt” to “blue shirt”) that affect only relevant regions, without disturbing the rest of the image.
- DreamBooth [537]: Targets personalization by finetuning a pretrained diffusion model on a small set of subject-specific images, anchored to a rare textual token (e.g., “sks”). This allows generation of images that retain the subject’s identity across diverse scenes and poses—crucial for creative professionals, avatars, or character preservation tasks.
- ControlNet [773]: Enables structural conditioning through auxiliary inputs like pose skeletons, depth maps, or edge detections. Crucially, it does so without modifying the base model by injecting trainable control paths that are fused with the original network. This unlocks precise spatial control and makes diffusion adaptable to external guidance from perception pipelines or user interfaces.
- IP-Adapter [733] and Transfusion [798]: Introduce modular, plug-and-play conditioning layers designed to adapt pretrained diffusion models to new visual or multimodal signals—without modifying the original weights. IP-Adapter uses a decoupled cross-attention mechanism that injects CLIP-derived image embeddings alongside frozen text features, enabling flexible image-guided generation, personalization, and cross-modal editing with only 22M trainable parameters. Transfusion builds on this adapter paradigm by unifying visual grounding with text and sketch modalities, enabling diverse zero-shot edits across tasks. Both approaches preserve the underlying text-to-image capabilities, making them well-suited for scalable, reusable, and composable image generation pipelines.
Collectively, these methods reframe diffusion models as interactive generation systems—capable of fine-grained control, identity preservation, and user-driven customization. The following sections delve into these approaches, starting with Prompt-to-Prompt, which introduced one of the first scalable solutions for semantically coherent prompt editing without sacrificing layout or visual consistency.
Enrichment 20.11.6: Prompt-to-Prompt (P2P): Cross-Attention Editing in DMs
Motivation and Core Insight Prompt-to-Prompt (P2P) [217] introduces a novel method for fine-grained, prompt-based image editing in text-to-image diffusion models. Unlike prior approaches that either operate directly in pixel space or require full model finetuning, P2P achieves precise semantic control by modifying only the prompt and reusing internal cross-attention maps of the diffusion process.
The core insight is that in text-conditioned diffusion models (e.g., Stable Diffusion), each token in the prompt corresponds to a spatial attention map over the latent image at every denoising step. These maps govern “what part of the image is controlled by which word”. By injecting stored attention maps for shared tokens between an original and edited prompt, P2P preserves image structure while applying meaningful semantic changes.
This mechanism allows users to:
- Replace entities (e.g., “a cat” \(\rightarrow \) “a dog”) while preserving the scene layout.
- Modify stylistic details (e.g., “a photo of a mountain” \(\rightarrow \) “a charcoal drawing of a mountain”).
- Tune the emphasis of individual adjectives or objects (e.g., increasing the visual weight of “snowy”).
P2P thus bridges the flexibility of prompt-based conditioning with the structural fidelity of spatial attention, enabling zero-shot edits with pixel-level consistency. In the following, we will explain how this method works, and see some usage examples.
Cross-Attention as the Mechanism for Prompt Influence In text-conditioned diffusion models such as Stable Diffusion, the U-Net backbone integrates the prompt via cross-attention layers at every denoising step \( t \in \{1, \dots , T\} \). At each step, the model maintains a latent representation \( \vec {z}_t \in \mathbb {R}^{h \times w \times d} \), where each of the \( N = h \cdot w \) spatial locations corresponds to a feature vector of dimension \( d \). This tensor is reshaped into a sequence \( \vec {z}_i \in \mathbb {R}^{N \times d} \), where each row \( \vec {z}_i[n] \) can be interpreted as encoding local information at spatial location \( n \) — similar to a pixel in a feature map, though potentially corresponding to a receptive field in the original image due to earlier convolutional layers.
Let the text prompt be tokenized into \( L \) tokens, each embedded into a vector \( \vec {e}_l \in \mathbb {R}^d \), forming an embedding matrix \( \vec {E} \in \mathbb {R}^{L \times d} \). These embeddings serve as the key-value memory bank over which the latent queries will attend. The cross-attention computation at each U-Net layer is then given by:
\[ \mbox{Attention}(\vec {z}_i, \vec {E}) = \mbox{softmax} \left ( \frac {Q K^\top }{\sqrt {d}} \right ) V, \]
where:
- \( Q = W_Q \vec {z}_i \in \mathbb {R}^{N \times d} \) are learned linear projections of the spatial feature vectors — one per location \( n \),
- \( K = W_K \vec {E}, \quad V = W_V \vec {E} \in \mathbb {R}^{L \times d} \) are the projected keys and values from the prompt token embeddings,
- \( A^t = \mbox{softmax} \left ( Q K^\top / \sqrt {d} \right ) \in \mathbb {R}^{N \times L} \) is the attention matrix at timestep \( t \).
If the original channel dimensions of \( \vec {z}_i \) or \( \vec {E} \) differ, the projections \( W_Q, W_K, W_V \) are used to map both inputs into a shared dimension \( d \), ensuring compatibility. These are learnable parameters trained end-to-end with the diffusion model.
Each entry \( A^t[n, l] \) quantifies how much the token \( w_l \) influences the generation at spatial position \( n \). This allows us to interpret the model as dynamically querying which parts of the prompt should affect which spatial regions of the latent representation.
We define the cross-attention map for token \( w_l \) at timestep \( t \) as: \[ M_l^t := A^t[:, l] \in \mathbb {R}^{N}, \] where \( A^t \in \mathbb {R}^{N \times L} \) is the cross-attention matrix at timestep \( t \), with \( N = h \times w \) denoting the number of spatial locations in the latent feature map and \( L \) the number of text tokens. The slice \( A^t[:, l] \) selects the attention weights from all spatial positions to the token \( w_l \), yielding a heatmap over image space that describes how strongly each location attends to the semantic concept expressed by \( w_l \).
This vector \( M_l^t \) can be reshaped into a 2D grid \( M_l^t \in \mathbb {R}^{h \times w} \) to match the spatial resolution of the U-Net features, allowing a visual interpretation of where token \( w_l \) is grounded at step \( t \). For example, if \( w_l = \mbox{``dog''} \), the corresponding map \( M_l^t \) will have high values in regions corresponding to the predicted dog’s body, such as its head or torso.
Concretely, if a spatial location \( i = (u, v) \) on the feature map has a high value \( M_l^t[u, v] \), it indicates that the pixel at location \( (u, v) \) in the latent representation is currently being influenced by, or aligned with, the semantics of the word “dog”. Thus, the cross-attention map captures the evolving alignment between text tokens and spatial regions throughout the diffusion process, enabling localized text-to-image control.
This attention mechanism forms the foundation for Prompt-to-Prompt’s editing capabilities: by storing the maps \( M_l^t \) from an initial prompt and reusing them selectively during generation with a modified prompt, one can tightly control how semantic concepts from the original image persist or change across edits. The next part describes how this editing mechanism is implemented.
Editing by Cross-Attention Injection Prompt-to-Prompt (P2P) [217] enables fine-grained, prompt-aware image editing by intervening in the cross-attention maps of a pre-trained text-to-image diffusion model. Given an original prompt \({p} = [w_1, \dots , w_L] \) and a revised prompt \({p}' = [w_1', \dots , w_{L'}'] \), the method aligns their token sequences and selectively manipulates attention maps \( M_l^t \) across diffusion timesteps \( t \in \{1, \dots , T\} \).
The core intuition is straightforward: each token \( w_l \) in the prompt attends to a spatial region in the image via its attention map \( M_l^t \), which evolves over time. If a token remains unchanged across prompts—e.g., “tree” in “a dog next to a tree” versus “a cat next to a tree”—then its associated spatial influence should also remain fixed. P2P enforces this consistency by injecting attention maps recorded during generation with the original prompt into the diffusion process guided by the new prompt.
By doing so, the method preserves image layout and semantic grounding for shared tokens, while allowing newly introduced or modified tokens to affect the image selectively.
This form of editing occurs at the cross-attention layers within the U-Net and can be controlled over time using a timestep threshold \( \tau \), enabling smooth interpolation between preservation and change.
The key components are:
- Attention Replacement for Matching Tokens: When a token \( w_l \in {p} \) appears identically in the edited prompt \( {p}' \), its attention map is replaced with the one recorded during generation of the original image: \[ M_l^{\prime t} \leftarrow M_l^t. \] This preserves the spatial layout and semantic grounding of the unchanged concept (e.g., “table” in both prompts “a red chair and a table” and “a blue chair and a table”).
-
Word Swapping via Timestep-Gated Attention Injection:
When a token in the prompt is replaced—for example, “car” \( \rightarrow \) “truck”—the goal is to modify the generated concept while keeping the rest of the image (e.g., layout, background, lighting) structurally intact. Prompt-to-Prompt (P2P) achieves this via a timestep-gated injection of cross-attention maps, controlled by a parameter \( \tau \), applied during the denoising process.
How it works: Diffusion models denoise a latent representation iteratively. At each timestep \( t \), cross-attention layers in the U-Net bind the current visual features (queries) to text tokens (keys and values). The resulting attention map \( M_l^t \in \mathbb {R}^{h \times w} \) for token \( w_l \) determines how strongly each spatial location should attend to that token.
Importantly, these maps encode where in the image each token is relevant—but not what the token means. The token’s semantic identity is carried through its embedding \( \vec {v}_l \), projected into the attention’s value vectors \( V \). During cross-attention, each spatial location receives a weighted sum of the values, using the attention map as weights: \[ \mbox{Output} = \hat {M}_l^t \cdot V_l^{\prime } \] In word swapping, P2P modifies the attention maps \( \hat {M}_l^t \) as follows: \[ \hat {M}_l^t = \begin {cases} M_l^{\prime t} & \mbox{if } t < \tau \quad \mbox{(use attention map from the new prompt)} \\ M_l^t & \mbox{if } t \geq \tau \quad \mbox{(inject original map from the old prompt)} \end {cases} \]
Why it works: Early in the diffusion process, the model determines the coarse structure—object layout, pose, and geometry. Using \( M_l^{\prime t} \) here ensures the new token (e.g., “truck”) can shape its own spatial identity, learning its approximate location and structure. Crucially, the values \( V_l^{\prime } \) always come from the new token embedding, so the semantic content being drawn from is never related to the original token (“car”).
Later in the process (\( t \geq \tau \)), the model begins refining texture, shading, and scene consistency. At this point, P2P injects the original attention maps \( M_l^t \) while still using the new values \( V_l^{\prime } \). This means the model is now told: “inject the semantic content of a truck, but do so in the spatial pattern where a car originally appeared.”
This is the crucial trick: the new concept (truck) inherits the spatial context of the old concept (car)—its location, size, and perspective—but none of its identity. There is no semantic leakage from the original word because the values, which carry the detailed information injected into the visual features, still come from the new prompt.
Example: When editing “a red sports car on a road” into “a red truck on a road,” early timesteps allow the attention of “truck” to shape its own geometry. After \( \tau \), the attention map of the original “car” is re-used, telling the model where in the image to continue refining. The resulting truck is structurally aligned with the original car’s pose and lighting, yet semantically distinct.
About the parameter \( \tau \): The transition point \( \tau \in [0, T] \) determines when control shifts from free composition to spatial anchoring. A smaller \( \tau \) gives more influence to the new prompt, allowing larger structural changes. A larger \( \tau \) preserves more of the original layout. In practice, intermediate values (e.g., \( \tau \approx 0.5 T \)) often strike a balance between visual fidelity and effective editing.
-
Adding New Phrases:
Suppose we augment the prompt from “a house in the snow” to “a house in the snow with a tree”. Our goal is to preserve the existing content (house, snow) while introducing the new concept (tree) in a natural and non-destructive way.
How it works: Let \( {p} \) and \( {p}' \) denote the original and edited prompts, respectively. At each timestep \( t \), Prompt-to-Prompt constructs the edited cross-attention maps \( \hat {M}_l^t \) as follows:
- For each token \( w_l \in {p} \cap {p}' \) that appears in both prompts, we inject the original attention map: \[ \hat {M}_l^t := M_l^t. \] This enforces spatial consistency for the unchanged concepts (e.g., “house”, “snow”).
- For each newly added token \( w_l \in {p}' \setminus {p} \), such as “tree”, we allow the model to compute its attention map normally: \[ \hat {M}_l^t := M_l^{\prime t}. \]
Why it usually works: This approach biases the generation toward preserving the original structure while carving out visual space for the new concept. The success of this balance depends on three factors:
- Preserved attention anchors: By freezing the attention maps for shared tokens, we ensure that their semantic influence remains fixed over the original image regions. This strongly encourages the model to reconstruct those regions similarly in the edited version.
- Limited interference by new tokens: Although new tokens can, in principle, influence any part of the image, their attention is typically focused on previously unclaimed or neutral areas—such as background space—where the frozen maps from shared tokens are weak. This is due to softmax normalization: strong attention weights from shared tokens crowd out competing influence from new ones in key regions.
- Value-weighted blending: Even when spatial attention overlaps, the injected attention maps act only as weights. The semantic content injected at each position still comes from the values—i.e., the token embeddings. Since the new token (“tree”) has distinct values from existing ones, its content will only dominate in regions where it receives sufficient attention. In most cases, this naturally confines it to appropriate areas without harming other objects.
Important caveat: This method is not foolproof. If a new token’s attention overlaps heavily with a shared token’s region, and its values inject strong or conflicting semantics, artifacts or unintended modifications can occur. However, such cases are rare in practice, especially for prompts that are incrementally edited or composed of semantically separable elements. Fine-tuning the diffusion guidance strength or manually constraining attention can further mitigate these risks.
Example: Inserting “a tree” into “a house in the snow” results in a tree appearing beside the house—often in the background or foreground—without shifting or deforming the house itself. The spatial layout and visual style of the original scene are preserved because the attention maps for “house” and “snow” remain fixed, shielding those areas from disruption.
-
Attention Re-weighting (Optional):
In prompts containing multiple concepts—such as “a cat on a chair with sunlight in the background”—we may wish to emphasize or suppress specific elements. For instance, one might want to intensify “sunlight” to brighten the scene or reduce the visual clutter associated with “background”. Prompt-to-Prompt enables this via a technique called attention re-weighting, also referred to as fader control.
How it works: Let \( j^* \) denote the index of the token to be modified, and let \( c \in [-2, 2] \) be a scaling coefficient. At each diffusion step \( t \), the cross-attention map \( M^t \in \mathbb {R}^{N \times L} \) from the original prompt’s generation is reweighted to obtain \( \hat {M}^t \), where each spatial position \( i \in \{1, \dots , N\} \) attends over the \( L \) tokens: \[ \hat {M}_{i,j}^t := \begin {cases} c \cdot M_{i,j}^t & \mbox{if } j = j^* \\ M_{i,j}^t & \mbox{otherwise} \end {cases} \] After reweighting, each row \( \hat {M}_{i,:}^t \) is typically renormalized (e.g., using softmax) to ensure the attention remains a valid distribution.
Why it works: Cross-attention determines where each token’s semantics are injected into the latent image during denoising. The weights \( M_{i,j}^t \) are used to combine the value vectors \( \vec {v}_j \) (from the token embeddings), controlling how much each token contributes at location \( i \). Increasing \( c \) boosts the pre-softmax score for token \( j^* \), which raises its relative weight after softmax: \[ \mbox{Softmax}(\hat {M}_{i,:}^t)[j^*] = \frac {e^{c M_{i,j^*}^t}}{\sum _{k=1}^{L} e^{\hat {M}_{i,k}^t}}. \] Thus, more pixels are drawn to the token’s semantic content, strengthening its influence. Conversely, reducing \( c \) weakens this effect.
Why it usually doesn’t disrupt other objects: Reweighting adjusts only a single token’s attention column. Since the attention is row-wise normalized, boosting one token proportionally reduces others—but only at spatial locations where that token already had influence. For unrelated concepts with disjoint spatial support, the impact is minimal. That said, large \( c \) values can overpower neighboring tokens in shared regions, potentially distorting their features.
Example: Increasing \( c \) for “sunlight” enhances brightness across attended regions, reinforcing highlights and atmospheric glow. Suppressing “background” with a low \( c \) reduces texture variation and visual noise, producing a cleaner, more focused composition.
These operations allow users to perform prompt-level edits—such as word substitution, phrase addition, or semantic emphasis—while preserving coherence, layout, and object identity in the image. Crucially, attention injection is not applied uniformly across the entire generation: the timestep threshold \( \tau \) allows for nuanced control over when the structure should be preserved and when it can adapt, striking a balance between faithfulness and flexibility.
This mechanism is particularly effective because it leverages the spatial grounding inherent in attention maps: regions influenced by unchanged words remain fixed, while edited words influence only localized changes. This permits high-fidelity image editing without requiring pixel-space operations or model retraining.
In the following, we demonstrate how this mechanism can modify object content, style, or structure while preserving layout.
Use Case: Content Modifications via Prompt Edits Once the Prompt-to-Prompt mechanism is in place, a natural application is controlled object substitution through prompt editing. For example, replacing “lemon cake” with “chocolate cake” or “birthday cake” should change only the appearance of the object itself while preserving the layout, lighting, and background structure.
The below figure demonstrates this use case. Starting from a baseline image generated from the prompt “lemon cake”, the prompt is modified to describe other cake types. Two editing strategies are compared:
- Top row (attention injection): P2P preserves the spatial layout of all shared words by copying their attention maps from the original generation. Only new tokens receive fresh attention maps.
- Bottom row (seed reuse only): The same random seed is reused, but no attention maps are injected — each prompt is generated independently.
In the attention-injected row, the cake’s pose, size, and plate remain stable across edits — the structure is preserved, and only semantic details (like texture and topping) change. Without attention injection, the geometry drifts significantly, resulting in inconsistent layouts.
This example highlights Prompt-to-Prompt’s ability to perform semantic transformations while preserving the geometric footprint of unchanged content — a key feature for controlled editing in image synthesis workflows.
We now turn to further use cases demonstrating Prompt-to-Prompt’s flexibility, including object preservation across scene changes, gradual injection strength for stylistic blending, and real-image editing via inversion.
Use Case: Object Preservation Across Scene Changes Prompt-to-Prompt also supports isolating and preserving a specific object from a source image while altering the rest of the scene. This is accomplished by selectively injecting the attention maps corresponding to a single token, such as “butterfly”, from the original prompt.
The below figure demonstrates how injecting only the attention maps of the word “butterfly” preserves its pose, structure, and texture across multiple edited prompts. The new contexts vary in composition and background — e.g., a room, a flowerbed, or abstract shapes — but the butterfly remains visually consistent, accurately positioned, and realistically integrated.
This type of localized control is especially useful for identity-preserving edits or compositional consistency — applications relevant to character animation, creative storytelling, and personalized image manipulation. It also sets the stage for more advanced use cases involving dynamic modulation of attention influence and real-image editing.
Use Case: Controlled Blending via Partial Attention Injection Prompt-to-Prompt enables fine-grained control over the generation process by specifying the temporal extent during which the original cross-attention maps are injected. By limiting attention replacement to only a subset of denoising timesteps \( \tau \in [0, T] \), users can navigate the trade-off between faithfulness to the edited prompt and fidelity to the original image structure.
Mechanism of control: Let \( \tau \in [0, T] \) be the timestep threshold at which attention injection transitions. For timesteps \( t < \tau \), the cross-attention maps computed from the edited prompt are used (encouraging semantic changes); for \( t \geq \tau \), the maps from the original prompt are injected (enforcing structural consistency). A small \( \tau \) means most steps rely on the original attention, preserving layout but potentially suppressing edits. A large \( \tau \) allows the new token’s semantics to dominate, which may yield better object replacement but increase spatial drift.
Why it matters: This mechanism allows users to blend the “what” (new concept) and “where” (original spatial anchors) over time, rather than committing to full replacement or preservation. For instance, replacing “car” with “bicycle” may succeed when injection occurs only after the early timesteps—letting the bicycle establish geometry, then snapping into the original scene’s pose and viewpoint.
This time-dependent attention editing proves useful in scenarios where both semantic change and structural stability are important. Applications include identity-preserving edits, fine-grained modifications to clothing or pose, and stylistic alterations that should respect background composition.
We now turn to complementary editing strategies that do not replace attention maps, but instead reweight them to modulate a token’s influence.
Use Case: Emphasizing and De-emphasizing Concepts Building on the principle of attention re-weighting, Prompt-to-Prompt enables dynamic emphasis or suppression of specific concepts directly through cross-attention manipulation. This allows users to subtly or dramatically control how visible or dominant a particular word becomes in the generated image—without changing the wording of the prompt itself.
In Figure 20.106, re-weighting is applied to highlight or downplay specific concepts. For example, increasing the attention mass on the token “fluffy” causes the entire image to exhibit more fluffiness in the texture of objects (in this example, the furry bunny doll). Conversely, reducing the attention weight on “blossom” attenuates the flower density and vibrancy of the tree canopy.
This flexible form of text-guided emphasis is useful in stylization, mood control, and semantic adjustment without prompt rewriting. The same technique can be applied for creative stylization.
Use Case: Text-Guided Stylization while Preserving Layout Prompt-to-Prompt enables text-guided stylization, allowing users to transform an image’s appearance while maintaining its spatial composition and semantic structure. This is achieved by appending stylistic descriptors (e.g., “charcoal sketch”, “futuristic illustration”) to the prompt while injecting the cross-attention maps from the original prompt. These injected maps anchor spatial localization, ensuring that stylistic changes affect only visual texture, tone, and color, not layout.
This strategy supports both sketch-to-photo and photo-to-sketch transformations, modulated entirely through text. By preserving structural attention, Prompt-to-Prompt ensures that stylistic changes remain localized to appearance, enabling faithful reinterpretations of the same scene across diverse visual domains. Such capabilities are valuable for domain adaptation, visual exploration, and iterative artistic workflows—offering a controllable, prompt-driven alternative to manual stylization or style transfer networks.
Use Case: Editing Real Images via Inversion and Prompt-to-Prompt Finally, Prompt-to-Prompt is not limited to synthetic images. By leveraging diffusion inversion techniques (e.g., DDIM inversion), real images can be mapped into latent noise vectors and edited as if they were generated samples. This extends the power of prompt-based editing to real-world inputs.
As shown in Figure 20.108, the inversion step maps a real photo (e.g., of a dog, house, or object) into a latent representation from which a faithful reconstruction can be generated. Prompt edits—such as changing the subject, adjusting appearance, or adding stylistic elements—are then applied via P2P. The result is an edited image that respects the original structure and layout but incorporates the semantic changes described in the updated prompt.
This capability opens the door to user-friendly image editing pipelines where real images can be modified through text alone, with fine-grained control over structure and content.
Limitations and Transition to Personalized Editing While Prompt-to-Prompt offers fine-grained control over textual edits through cross-attention injection, re-weighting, and temporal scheduling, it still inherits several limitations from the underlying diffusion framework:
- Vocabulary-bound concept control: P2P assumes that all visual elements in the scene are represented by prompt tokens. Consequently, it cannot edit or preserve objects that lack a direct textual grounding—such as a specific person’s face, a custom logo, or a unique product design.
-
Semantic drift with underrepresented concepts: For rare or ambiguous tokens (e.g., “blossom”, “rustic”, or abstract modifiers like “ethereal”), the associated value vectors may not fully capture the desired visual features. As a result, cross-attention editing may be inconsistent, yielding unpredictable outputs or semantic drift over time.
- Limited identity preservation: Because Prompt-to-Prompt relies purely on manipulating cross-attention weights, it cannot preserve fine-grained visual identity—such as the facial features of a specific subject—when editing real images. As demonstrated in prior sections, even when using DDIM inversion to anchor the source image in latent space, significant details may be lost or altered during generation.
These limitations motivate the need for personalized fine-tuning techniques that go beyond attention manipulation. In particular, to faithfully edit scenes involving novel or user-defined subjects—such as a specific dog, a unique sculpture, or a person’s face—we require models that can learn new visual concepts and bind them to custom textual tokens.
While Prompt-to-Prompt enables fine-grained control over structure and style through attention manipulation, it remains limited to concepts already understood by the base model. It cannot synthesize entirely new identities or visually-grounded concepts absent from the training data. This motivates the need for subject-driven generation, where the model is explicitly taught to recognize and recreate a particular instance—such as a person, object, or pet—across diverse prompts and settings.
This leads us to DreamBooth [537], a technique for high-fidelity personalization via instance-specific fine-tuning. DreamBooth introduces a unique token (e.g., “[V]”) into the model’s vocabulary and trains the model to associate it with the visual identity of a particular subject using just a handful of example images. Once embedded, this token can be flexibly composed with other text descriptors to guide generation across different poses, environments, and styles—all while preserving core identity traits.
In the following, we explore how DreamBooth achieves this level of instance control, what challenges arise in balancing identity preservation with prompt diversity, and how its innovations laid the groundwork for personalized diffusion models.
Enrichment 20.11.7: DreamBooth: Personalized Text-to-Image Generation
Motivation and Core Insight DreamBooth [537] proposes a method for customizing pretrained text-to-image diffusion models—such as Stable Diffusion or Imagen—so that they can generate realistic, context-aware, and stylistically diverse images of a specific subject, using only a handful of example images.
The key challenge addressed by DreamBooth is as follows: while large diffusion models are trained on broad distributions of internet-scale data, they cannot reliably synthesize faithful renditions of an individual subject (e.g., a specific dog or product) unless it appeared in their training data, and with a unique identifier that allows reconstruction in various settings. Simply prompting with ”a dog on a beach” might yield a generic canine, but not your dog.
To solve this, DreamBooth introduces the idea of binding a unique textual identifier—such as sks—to a novel visual subject by fine-tuning the diffusion model on a small set of subject-specific images paired with customized prompts (e.g., ”a photo of a sks dog”). This enables the model to learn the association between the identifier and the subject’s visual concept, allowing the generation of high-fidelity outputs in new poses, scenes, or styles using just prompt-based control.
This mechanism builds toward a more general idea in controllable generation: associating visual attributes with tokens in the text space and using prompt engineering to drive structured edits. In later works, we will see how ControlNet extends this idea further by conditioning on spatial inputs like edges or poses. But first, we will examine how DreamBooth establishes the foundational capability of subject-driven customization using only a few images and simple text.
Model Setup and Identifier Creation DreamBooth [537] modifies large pretrained text-to-image diffusion models—such as Stable Diffusion and Imagen—to enable personalized subject-driven generation. Given only a handful of subject reference images (typically 3–5), DreamBooth introduces a new textual identifier that serves as a symbolic stand-in for the subject. By finetuning the model on prompts like "a sks dog in the snow", the model learns to associate the rare token sks with the subject’s visual appearance. This enables prompt-driven recontextualization of the subject across new scenes, poses, and styles.
The model architecture remains intact, with only a targeted subset of parameters updated during training:
- Frozen Text Encoder: The input prompt is tokenized and embedded by a pretrained encoder—e.g., CLIP for Stable Diffusion or T5-XXL for Imagen. These components remain fixed throughout training.
- Frozen Image Encoder/Decoder: Stable Diffusion uses a pretrained VAE to map RGB images to a lower-dimensional latent space. Imagen, in contrast, operates directly in pixel space using a base model and super-resolution stages. In both cases, these modules are left untouched.
- Trainable U-Net Denoiser: The U-Net receives noisy inputs (pixels or latents), a timestep embedding, and cross-attention conditioning from the prompt. This is the only component that is finetuned during DreamBooth training, learning to associate the rare subject token with its corresponding visual appearance.
To introduce a new subject into the model’s vocabulary, DreamBooth selects a unique rare token \( \mathbf {s} \), such as sks, and uses it in prompts of the form:
\[ \texttt{"a photo of a } \underbrace {\texttt{sks}}_{\mbox{subject ID}} \underbrace {\texttt{dog}}_{\mbox{class label}} \texttt{"} \]
This prompt is paired with each training image of the subject. During finetuning, the model learns to associate the identifier sks with the subject’s unique appearance while preserving the general semantics of the class label (e.g., dog).
Identifier Token Selection Strategy
The effectiveness of DreamBooth hinges on selecting a subject token \( \mathbf {s} \) that is both learnable and semantically disentangled—meaning it has weak or no associations with existing concepts in the model’s pretraining distribution. If \( \mathbf {s} \) corresponds to a token that is already semantically rich (e.g., ”dog”, ”person”, ”red”), fine-tuning may corrupt unrelated concepts (semantic drift) or introduce identity leakage and reduced generative diversity. Conversely, if \( \mathbf {s} \) is rarely used during pretraining, the model is free to associate it entirely with the new subject.
Tokenizer Overview and Motivation
Like most modern text-to-image models, DreamBooth processes natural language prompts using a tokenizer—a component that maps raw text into a sequence of discrete token IDs. These IDs form the input to the model’s text encoder and are drawn from a fixed vocabulary that is constructed during pretraining on a large-scale corpus.
Rather than operating at the level of individual characters or entire words, modern tokenizers segment text into subword units—variable-length fragments like “red”, or “xxy5”. This subword decomposition strikes a practical balance between expressiveness and efficiency:
- It avoids the combinatorial explosion of full-word vocabularies, which would require millions of entries to cover rare terms, compound words, or typos.
- It reduces the sequence length relative to character-level tokenization, thereby improving model efficiency and allowing for longer contextual understanding.
- It ensures robustness: even unseen or rare words can still be represented using known fragments from the vocabulary.
The result is a compact, reusable, and expressive vocabulary that allows any input string—no matter how unusual—to be tokenized into a valid sequence of known token IDs. Each token ID is then mapped to a high-dimensional embedding vector via a static lookup table in the text encoder. These embeddings are passed through a Transformer-based architecture such as CLIP or T5 to produce contextualized representations used to condition the image generation process.
During image generation, particularly in diffusion-based architectures, the contextualized text embeddings influence visual outputs through dedicated cross-attention layers. These layers are embedded within the model’s U-Net architecture and act as an interface between the text encoder and the evolving image representation. Specifically, visual features derived from the noisy image (acting as attention queries) attend to the token-level embeddings (acting as keys and values), producing spatially localized responses. The result is a set of attention maps that modulate each region of the image according to its relevance to the corresponding text tokens.
This mechanism establishes a direct spatial-semantic correspondence: each region of the image learns to ”pay attention” to the appropriate linguistic concepts in the prompt. Such alignment is foundational for accurate text-to-image synthesis. In DreamBooth, this correspondence is further exploited during fine-tuning—where a rare identifier token is explicitly trained to control the appearance of a novel subject. The gradients from the cross-attention pathway reinforce the association between that token and spatial structures in the generated image, enabling the model to synthesize consistent and editable subject representations in response to prompt variations.
Rare Token Selection for Subject Identity Binding
DreamBooth performs subject personalization without altering the tokenizer or the text encoder. Instead of introducing new vocabulary, it repurposes an existing but underused token \( s_{\mbox{text}} \) from the tokenizer’s fixed vocabulary to symbolically represent a novel subject. This token’s embedding—denoted \( \vec {e}_s \in \mathbb {R}^d \)—is static, produced by the frozen text encoder, and interpreted only by the fine-tuned diffusion model (e.g., the U-Net).
The goal is to choose a token that behaves as a semantic blank slate: syntactically valid, visually neutral, and semantically unentangled. The U-Net is then trained to associate \( \vec {e}_s \) with the personalized subject appearance while leaving the text encoder entirely untouched. After training, prompts like "a sks dog in the snow" can reliably generate identity-consistent outputs in diverse contexts.
The rare-token selection strategy is general and applies to any text encoder–tokenizer pair. Below we outline a unified procedure applicable to both Imagen (using T5 with SentencePiece) and Stable Diffusion (using CLIP with Byte-Pair Encoding).
- 1.
- Enumerate the Tokenizer Vocabulary.
Each tokenizer defines a fixed mapping from token IDs to Unicode strings:- Imagen uses T5-XXL with a SentencePiece vocabulary of size 32,000.
- Stable Diffusion uses a CLIP-BPE tokenizer with approximately 49,000 tokens.
These mappings can be accessed via tokenizer APIs.
- 2.
- Identify Rare, Neutral Candidates.
The ideal token \( s_{\mbox{text}} \) is rare (low frequency) and lacks meaningful associations. For example:- In Imagen, token IDs in the range \[ \{5000, 5001, \ldots , 10000\} \] are empirically found to be infrequent in the training corpus and often decode to short, nonsensical strings like sks, qxl, or zqv.
- In Stable Diffusion, naive strings like sks may be split into multiple tokens unless formatted with brackets (e.g., [sks]) to ensure they are tokenized as a single unit.
- 3.
- Filter Structurally Valid Tokens.
Candidate tokens must satisfy the following constraints:- Decodability: The token maps to a valid, printable Unicode string.
- Length: Ideally 1–3 characters or a compact glyph.
- Token integrity: It must remain a single token after tokenization.
- Semantic neutrality: It should not resemble common words, brand names, or known entities.
Once a valid token is chosen, it is held fixed and used in all subject-specific prompts during DreamBooth finetuning. The text encoder produces a static embedding \( \vec {e}_s \), while only the U-Net learns to interpret it as the visual identity of the subject. This setup supports prompt compositionality, enabling queries like:
- "a watercolor painting of a sks vase in a spaceship"
- "a sks dog painted by Van Gogh"
- "a sks backpack on the Moon"
In summary, the reuse of rare tokens provides an elegant, encoder-compatible mechanism for subject binding. By leveraging frozen embeddings with minimal prior entanglement, DreamBooth enables high-fidelity personalization while preserving the expressive power of the original generative model.
In the following, we describe how this token selection integrates into the full DreamBooth training procedure, including loss functions that ensure both precise subject encoding and generalization to new contexts.
Training Objective and Prior Preservation Once a rare identifier token \( s_{\mbox{text}} \) has been selected and inserted into structured prompts, DreamBooth fine-tunes the pretrained text-to-image model to associate the subject with its corresponding static embedding \( \vec {e}_s \). Training follows the denoising diffusion paradigm, augmented with a regularization term that preserves the model’s generative flexibility.
Main Loss: Denoising Objective Let \( \{x_1, x_2, \dots , x_n\} \) denote a small subject dataset, and let each image \( x_i \) be paired with a prompt \( y_i = \texttt{"a photo of a } s_{\mbox{text}} \texttt{ class"} \). The fine-tuning process proceeds as follows:
- 1.
- Encode each image \( x_i \) using the frozen image encoder:
- For LDMs: obtain latent representation \( \vec {z}_i = \mbox{Enc}(x_i) \).
- For pixel-space models (e.g., Imagen): use \( \vec {z}_i = x_i \).
- 2.
- Sample a timestep \( t \sim \mathcal {U}(\{1, \dots , T\}) \) and corrupt the input: \[ \vec {z}_{i,t} = \sqrt {\bar {\alpha }_t} \vec {z}_i + \sqrt {1 - \bar {\alpha }_t} \, \vec {\epsilon }, \quad \vec {\epsilon } \sim \mathcal {N}(0, \vec {I}). \]
- 3.
- Encode the prompt \( y_i \) using the frozen text encoder to obtain embeddings \( \vec {E}_i \), where \( \vec {e}_s \in \vec {E}_i \) denotes the token embedding of \( s_{\mbox{text}} \).
- 4.
- Input \( (\vec {z}_{i,t}, t, \vec {E}_i) \) into the U-Net and predict the noise: \[ \hat {\vec {\epsilon }} = \mbox{U-Net}(\vec {z}_{i,t}, t, \vec {E}_i). \]
- 5.
- Minimize the reconstruction loss: \[ \mathcal {L}_{\mbox{recon}} = \left \| \hat {\vec {\epsilon }} - \vec {\epsilon } \right \|_2^2. \]
During this process, only the U-Net parameters (and optionally its cross-attention layers) are updated. The tokenizer, text encoder, and VAE remain frozen.
Preventing Overfitting: Prior Preservation Loss Since DreamBooth typically trains on as few as 3–5 images, it is prone to overfitting—resulting in memorized poses, lighting, or background, and catastrophic forgetting of class diversity. To mitigate this, DreamBooth introduces a prior preservation loss that encourages the model to retain generative variability across the subject’s class.
This is implemented by mixing in a batch of generic class instances:
- For each batch, sample additional images \( \{x^{\mbox{prior}}_j\} \) with prompts like "a photo of a dog", omitting the identifier token.
- Apply the same forward corruption process and compute the corresponding loss: \[ \mathcal {L}_{\mbox{prior}} = \left \| \hat {\vec {\epsilon }}_{\mbox{prior}} - \vec {\epsilon } \right \|_2^2. \]
The final training objective becomes: \[ \mathcal {L}_{\mbox{total}} = \mathcal {L}_{\mbox{recon}} + \lambda \cdot \mathcal {L}_{\mbox{prior}}, \] where \( \lambda \in \mathbb {R}_+ \) controls the strength of prior preservation (typically \( \lambda = 1.0 \)).
Effect and Interpretation The prior-preservation term acts as a semantic constraint: it encourages the model to treat the identifier \( s_{\mbox{text}} \) as a distinct instance within a broader class, rather than as a class replacement. This enables:
- Preserves the model’s ability to generate diverse class-consistent outputs (e.g., dogs in snow, with accessories, or in unusual settings).
- Enables identity-grounded generation in novel contexts—e.g., "a sks dog in the desert", "a sks dog jumping over a fence", or "a sks dog wearing sunglasses".
This balance between memorization and generalization is critical for subject-driven generation to remain flexible and compositional. In the following, we explore how DreamBooth leverages this setup to enable high-fidelity identity transfer across scenes, styles, and visual manipulations.
Subject-Driven Generation in New Contexts Once DreamBooth has successfully fine-tuned the model to bind a unique token \(\mathbf {s}\) to a subject identity, it can be used to generate photorealistic or stylized images of that subject in a wide range of scenarios. Unlike traditional overfitted fine-tuning techniques, DreamBooth supports rich recontextualization—the subject can be rendered in scenes it was never observed in, under varying lighting conditions, poses, styles, and semantic compositions.
This capability is made possible by the model’s retained understanding of the subject’s class (e.g., “teapot”, “dog”)—due to the prior preservation loss—and the flexibility to modify the subject’s expression, pose, or style through text prompts:
- \a sks dog crying", \a sks dog sleeping", \a sks dog smiling" — expression manipulation
- \a Van Gogh painting of a sks dog" — style transfer
- \a sks dog with wings", \a sks dog in the style of a sculpture" — compositional attributes
DreamBooth also supports zero-shot outfitting and attribute additions. Guided by prompt text, the model composes realistic physical interactions between the subject and newly specified objects, outfits, or environments.
By decoupling the subject embedding \(\mathbf {s}\) from specific backgrounds, poses, and lighting, DreamBooth enables flexible recombination with diverse prompts. This supports high-fidelity identity preservation across scenes, compositions, and artistic styles—unlocking broad applications in personalized content creation, from digital avatars and branded photography to stylized storytelling.
These capabilities highlight DreamBooth’s ability to interpolate both pose and rendering domain. Viewpoint shifts and stylistic alterations—unseen in the training images—are synthesized faithfully while retaining fine-grained subject detail. This extends the model’s generative capacity far beyond memorization.
Nonetheless, DreamBooth is not without limitations. Some failure modes arise in rare contexts, entangled prompts, or when the model overfits to specific image details.
While DreamBooth achieves impressive subject fidelity, it often struggles with precise compositional control. Issues such as background entanglement, pose collapse, or implausible scene generation persist—especially when attempting to render the subject in unfamiliar contexts. Prompt-to-Prompt [217] addressed some of these shortcomings by manipulating cross-attention maps to steer how specific words influence spatial regions of the image. However, its control remains fundamentally implicit—limited to prompt structure and lacking direct spatial supervision.
This motivates a shift toward explicit conditioning: instead of relying solely on text, can we guide generation using structured visual signals such as edge maps, depth fields, or pose skeletons? ControlNet provides a powerful answer to this question. By injecting auxiliary control encoders into the diffusion backbone, ControlNet enables fine-grained spatial, geometric, and semantic modulation of the generation process—dramatically improving compositional accuracy and unlocking new applications in image editing, synthesis, and personalized rendering.
In the following, we examine the architecture, training procedure, and capabilities of ControlNet, highlighting how it can be used independently or in conjunction with methods like DreamBooth to enhance controllability and visual grounding.
Enrichment 20.11.8: ControlNet – Structured Conditioning for Diffusion Models
Motivation and Background Despite the remarkable success of prompt-based diffusion models in generating photorealistic and semantically coherent images, they offer only coarse-grained control over the structure and layout of the output. Natural language prompts—such as “a person riding a bicycle near the ocean”—are inherently ambiguous in spatial and geometric terms. As a result, generated scenes may omit critical elements, produce anatomically implausible poses, or fail to match user intent in fine-grained ways.
This limitation stems from the fact that text alone cannot precisely encode spatial or visual structure. Concepts such as object pose, layout, depth, or boundaries are difficult to express in natural language and even harder for the model to ground consistently. Methods like DreamBooth [537] improve subject identity preservation, and techniques such as Prompt-to-Prompt [217] allow for localized prompt manipulation via attention maps—but both approaches rely solely on textual cues and offer no mechanism for incorporating structured visual guidance.
To address these challenges, ControlNet [773] introduces a principled architectural extension to diffusion models that enables conditioning on external visual signals. These conditioning inputs—such as edge maps, human poses, depth estimates, scribbles, or segmentation masks—serve as explicit spatial priors, providing the model with structured cues that text alone cannot supply. For example, a depth map can enforce perspective geometry in a 3D interior scene, while a pose skeleton can define limb orientation and articulation in human generation tasks.
ControlNet thus empowers users to inject high-level semantic intent through text while simultaneously guiding low-level spatial structure via visual hints—bridging the gap between language-driven generation and precise, user-defined control over image composition.
This capability is especially important in domains where spatial layout matters—such as:
- Pose-to-image generation (e.g., rendering a person performing a specific action).
- Edge-to-photo synthesis (e.g., recreating objects from sketches).
- Semantic-to-scene mapping (e.g., transforming segmentation maps into photorealistic scenes).
By introducing minimal architectural overhead and preserving the core capabilities of the base diffusion model, ControlNet bridges the gap between prompt conditioning and structured visual control. In the following, we will examine its design, training procedure, and practical benefits.
Block Injection and Architectural Motivation ControlNet augments large pretrained text-to-image diffusion models—such as Stable Diffusion—by introducing a trainable conditional branch designed to interpret external structural cues (e.g., edge maps, depth, pose, segmentation) while preserving the integrity of the base model. These external cues are encoded as condition maps \( c \in \mathbb {R}^{H \times W \times C} \), and are used in conjunction with the usual text prompt \( y \), forming a dual conditioning scheme:
- The text prompt is tokenized and encoded by a frozen text encoder (e.g., CLIP), producing embeddings that are injected into the U-Net via cross-attention layers.
- The condition map is passed through a dedicated encoder, whose outputs are injected into a trainable replica of the U-Net blocks, spatially guiding generation at each resolution.
ControlNet’s integration with large-scale pretrained diffusion models represents a significant architectural innovation. Rather than retraining a diffusion model from scratch—a process that would require massive datasets like LAION-5B [556], which are tens of thousands of times larger than typical condition-specific datasets—ControlNet employs a far more efficient strategy.
It locks the parameters of a production-ready model, such as Stable Diffusion [531], thereby preserving its high-fidelity generation capabilities acquired through training on billions of image–text pairs. Simultaneously, it introduces a trainable replica of each internal block in the U-Net backbone. These replicas allow the model to adapt to new forms of spatial or structural conditioning (e.g., edges, depth, pose) without disrupting the semantics encoded in the original weights. This approach avoids overfitting and catastrophic forgetting—common pitfalls in low-data fine-tuning scenarios [350].
A key architectural mechanism enabling this safe dual-path design is the use of zero convolutions [773]. These are \(1 \times 1\) convolution layers whose weights and biases are initialized to zero. As a result, the conditional branches contribute nothing at the beginning of training, ensuring that the pretrained activations remain untouched. Gradually, as gradients update these layers, the conditional signal is introduced in a controlled, non-disruptive manner. This guarantees a stable warm-start and protects the pretrained backbone from the destabilizing effects of random gradient noise early in training.
Enrichment 20.11.8.1: ControlNet Architecture
Injecting Spatial Conditioning into Frozen Networks Large-scale pretrained models such as the U-Net used in Stable Diffusion exhibit remarkable generative capabilities, especially when guided by text prompts. However, their reliance on linguistic conditioning alone limits their ability to follow spatial instructions—such as replicating object pose, structural contours, or depth information—especially in tasks requiring precise layout control. This gap motivates the development of ControlNet, a framework that injects spatial condition maps into the intermediate layers of a frozen pretrained diffusion model, enabling fine-grained control while preserving generative quality.
Let \( \mathcal {F}(\cdot ; \Theta ) \) denote a frozen network block, where a block refers to a modular transformation unit such as a residual block or Transformer layer. Given an input feature map \( x \in \mathbb {R}^{H \times W \times C} \), the block produces an output feature map \( y = \mathcal {F}(x; \Theta ) \). These feature maps encode semantically and spatially rich representations used progressively in denoising-based generation.
ControlNet Architectural Design To augment the network with conditioning, ControlNet associates each frozen block \( \mathcal {F}(\cdot ; \Theta ) \) with a trainable replica \( \mathcal {F}(\cdot ; \Theta _c) \). This replica processes both the original feature map \( x \) and an external condition map \( c \in \mathbb {R}^{H \times W \times C} \), such as a Canny edge image, depth map, or human pose keypoints. The condition map is transformed into a residual signal through a pair of zero-initialized \( 1 \times 1 \) convolution layers:
\begin {equation} y_c = \mathcal {F}(x; \Theta ) + \mathcal {Z} \left ( \mathcal {F}\left (x + \mathcal {Z}(c; \Theta _{z1}); \Theta _c \right ); \Theta _{z2} \right ) \end {equation}
Here, \( \mathcal {Z}(\cdot ; \Theta _{z1}) \) injects the condition into the input space of the trainable replica, while \( \mathcal {Z}(\cdot ; \Theta _{z2}) \) modulates the output. Both zero convolutions are initialized such that their weights and biases are exactly zero, ensuring that the condition path introduces no change at the start of training.
Motivation for Additive Injection: Why Not Inject \( c \) Directly? A seemingly natural idea would be to inject the condition map \( c \) directly into the layers of the frozen U-Net—via concatenation, addition, or feature fusion. However, this naive approach often results in degraded output quality. The pretrained model encodes subtle statistical priors learned from billions of image-text pairs. Tampering with these internal representations, especially with limited data and abrupt injections, may cause:
- Catastrophic Forgetting: Directly modifying the feature flow may cause the model to forget its generative priors, reducing sample diversity and fidelity.
- Semantic Drift: Uncontrolled condition injection can skew the model’s internal representations, leading to mismatches between prompts and outputs.
- Training Instability: The injection introduces mismatched signals, leading to noisy gradients and divergence during optimization.
ControlNet avoids these pitfalls by enforcing architectural separation: the condition map \( c \) flows through a parallel, trainable branch that computes residual corrections to the output of the frozen U-Net. These corrections are injected additively via zero-initialized \( 1 \times 1 \) convolutions, ensuring that pretrained knowledge remains unperturbed at the start of training. This design enables progressive alignment, where the residuals only modify the output when helpful.
- \( \mathcal {F}(x; \Theta ) \): The original U-Net block with frozen weights \( \Theta \), trained on large-scale image-text data and reused without modification.
- \( \mathcal {F}(x'; \Theta _c) \): A trainable replica of the frozen block, receiving a perturbed input \( x' = x + \mathcal {Z}(c; \Theta _{z1}) \), where \( \mathcal {Z} \) is a zero-initialized convolution.
- \( \mathcal {Z}(\cdot ; \Theta _{z1}) \), \( \mathcal {Z}(\cdot ; \Theta _{z2}) \): Zero-initialized \(1 \times 1\) convolutions used at the input and output of the trainable path, regulating the influence of the conditional signal.
How Can the Output Change If the U-Net Is Frozen? And Why Is Denoising Still Valid? Freezing the U-Net implies that its output remains unchanged—but ControlNet introduces a trainable parallel path that circumvents this limitation. At each U-Net block, a residual branch is appended and fused with the frozen output via zero-initialized \( 1 \times 1 \) convolutions:
\begin {equation} y_c = \mathcal {F}(x; \Theta ) + \mathcal {Z}_2 \left ( \mathcal {F}(x + \mathcal {Z}_1(c; \Theta _{z1}); \Theta _c); \Theta _{z2} \right ) \end {equation}
Initially, both \( \mathcal {Z}_1 \) and \( \mathcal {Z}_2 \) are zero-initialized, making \( y_c = \mathcal {F}(x; \Theta ) \)—identical to the pretrained model. This ensures a safe warm start that avoids destabilization.
Although the residual branches in ControlNet are initialized with zero convolution layers—meaning all weights \( W \) and biases \( B \) are set to zero at the beginning of training—they remain fully trainable. The forward pass of such a layer for an input feature map \( I \in \mathbb {R}^{H \times W \times C} \) is defined as:
\begin {equation} Z(I; \{W, B\})_{p,i} = B_i + \sum _j I_{p,j} W_{i,j} \end {equation}
At initialization, since \( W = 0 \) and \( B = 0 \), the output is zero. However, the gradients behave as follows (where \( \frac {\partial \mathcal {L}}{\partial Z} \) denotes the upstream gradient):
\begin {align} \frac {\partial Z(I; \{W, B\})_{p,i}}{\partial B_i} &= 1 \\ \frac {\partial Z(I; \{W, B\})_{p,i}}{\partial I_{p,i}} &= \sum _j W_{i,j} = 0 \\ \frac {\partial Z(I; \{W, B\})_{p,i}}{\partial W_{i,j}} &= I_{p,j} \end {align}
We see that while the gradient with respect to the input \( I \) is zero initially (due to \( W = 0 \)), the gradients with respect to the bias \( B \) and the weights \( W \) are non-zero as long as the input feature \( I \) itself is non-zero—which is always the case in practice, since \( I \) encodes the image or conditioning information.
This mechanism ensures that the first gradient descent step will update the weights to non-zero values. For example, assuming a non-zero learning rate \( \beta _{\mbox{lr}} \) and loss gradient \( \partial \mathcal {L} / \partial Z \neq 0 \), the weight update becomes:
\begin {equation} W^* = W - \beta _{\mbox{lr}} \cdot \left ( \frac {\partial \mathcal {L}}{\partial Z} \odot \frac {\partial Z}{\partial W} \right ) \end {equation}
where \( \odot \) denotes the Hadamard (elementwise) product. After this step, the weight matrix \( W^* \) becomes non-zero, and the layer begins to propagate gradients to its input as well:
\begin {equation} \frac {\partial Z(I; \{W^*, B\})_{p,i}}{\partial I_{p,j}} = \sum _j W^*_{i,j} \neq 0 \end {equation}
Training Objective ControlNet is fine-tuned using the standard diffusion loss, augmented to include both spatial and textual conditioning. This objective trains the model to predict the noise added to a latent image representation at a given timestep, while also respecting high-level textual and low-level spatial guidance.
Each training sample includes:
- \( z_0 \): Clean latent representation, encoded from a \(512 \times 512\) image using a frozen VQ-GAN encoder [148, 531].
- \( \epsilon \sim \mathcal {N}(0, I) \): Gaussian noise.
- \( t \in \{1, \ldots , T\} \): Diffusion timestep.
- \( z_t = \sqrt {\bar {\alpha }_t} z_0 + \sqrt {1 - \bar {\alpha }_t} \, \epsilon \): Noised latent using cumulative schedule \(\bar {\alpha }_t\).
- \( c_t \): Text embedding from a frozen encoder (e.g., CLIP) [498]. During training, 50% of prompts are replaced with empty strings to promote reliance on spatial inputs [773].
- \( c_i \): Spatial condition image (e.g., pose, depth, edges) deterministically derived from \(z_0\).
- \( c_f = \mathcal {E}_{\mbox{cond}}(c_i) \): Feature map from a shallow encoder \(\mathcal {E}_{\mbox{cond}}\), aligned to U-Net resolution.
The loss function is: \begin {equation} \mathcal {L}_{\mbox{ControlNet}} = \mathbb {E}_{z_0, t, \epsilon , c_t, c_f} \left [ \left \| \epsilon - \epsilon _\theta (z_t, t, c_t, c_f) \right \|_2^2 \right ] \label {eq:controlnet_loss} \end {equation}
Why ControlNet Preserves Denoising Capability ControlNet extends pretrained diffusion models with spatial guidance while preserving their original denoising behavior. This is achieved through a design that carefully introduces conditional influence without interfering with the U-Net’s pretrained functionality.
At the heart of the diffusion process lies a U-Net trained to predict noise across billions of images [531]. In ControlNet, this U-Net is left entirely frozen during training [773], meaning it continues to perform the same denoising task it was originally optimized for. The key innovation lies in how ControlNet introduces its new functionality: by attaching a parallel, trainable branch whose outputs are added to the internal feature maps of the frozen U-Net at each resolution [773].
Initially, this residual branch is non-functional. All connecting \(1 \times 1\) convolution layers are zero-initialized—both weights and biases—which guarantees that the trainable path contributes no signal at the beginning. Thus, the model’s forward pass and denoising predictions are initially identical to the pretrained backbone. Crucially, despite being inactive at first, these zero-initialized layers admit nonzero gradients with respect to both their weights and biases. As long as the input condition maps contain nonzero values (which they typically do), gradient descent immediately begins to train the ControlNet branch—starting from a neutral baseline and gradually learning how to steer the generation process.
This training strategy ensures that conditional guidance is introduced in a progressive and reversible way. Because the U-Net remains frozen, the core noise prediction function is never corrupted. Instead, ControlNet learns to produce residual corrections that refine the denoising trajectory in a way that respects both the diffusion objective and the spatial constraints imposed by the conditioning input. The result is a denoising model that continues to predict valid noise estimates, now informed by an auxiliary signal such as an edge map or pose skeleton.
In essence, ControlNet does not replace the original model’s logic—it learns to nudge it. The trainable branch aligns the latent noise prediction with external guidance, but the primary computation and structure of the denoising process remain governed by the fixed U-Net. This preserves the quality, stability, and generalization of the pretrained model while enabling precise spatial control.
We now continue focusing on ControlNet’s training dynamics, sudden convergence behavior, and the role of Classifier-Free Guidance (CFG):
Enrichment 20.11.8.2: Training Behavior and Sudden Convergence
A key strength of ControlNet’s architectural design lies in its training stability. Thanks to the zero-initialized convolution layers that bridge the frozen and trainable branches, the model behaves identically to the original Stable Diffusion at initialization. This ensures that the first forward passes produce coherent images, even before any optimization occurs.
As training progresses, gradients propagate through the zero convolutions and update the trainable ControlNet branches. Initially, these branches exert no influence on the output. However, within a few thousand training steps, a phenomenon referred to as sudden convergence emerges: the ControlNet rapidly learns to inject the condition map into the generation process in a semantically meaningful way.
This behavior reflects the progressive unfreezing of the control pathway: the zero-initialized convolutions learn how to linearly transform the conditioned features to guide generation, while the trainable U-Net blocks learn to interpret the condition map. Throughout this process, the frozen base model remains intact, continuing to produce high-quality visual content.
Classifier-Free Guidance and Resolution-Aware Weighting ControlNet enhances the capabilities of diffusion models by integrating Classifier-Free Guidance (CFG) [224], a technique that balances adherence to conditioning inputs (like text prompts) with the diversity and realism of generated images. Additionally, ControlNet introduces a novel refinement: Classifier-Free Guidance Resolution Weighting (CFG-RW), which dynamically adjusts guidance strength across different spatial resolutions to optimize both semantic alignment and visual fidelity.
Classifier-Free Guidance (CFG) that we’ve covered in Enrichment 20.9.3 operates by training the diffusion model to handle both conditional and unconditional scenarios. During training, the conditioning input (e.g., text prompt \( y \)) is randomly omitted in a subset of training instances (commonly 50%), compelling the model to learn representations that are robust to the absence of explicit conditions. At inference, the model combines the conditional prediction \( \epsilon _{\mbox{cond}} \) and the unconditional prediction \( \epsilon _{\mbox{uncond}} \) using a guidance scale \( \lambda \):
\[ \epsilon _{\mbox{CFG}} = \epsilon _{\mbox{uncond}} +\lambda \cdot (\epsilon _{\mbox{cond}} - \epsilon _{\mbox{uncond}}) \]
This formulation allows users to modulate the influence of the conditioning input, with higher values of \( \lambda \) enforcing stronger adherence to the condition, potentially at the cost of image diversity.
Resolution-Aware Weighting (CFG-RW) Resolution-Aware Weighting (CFG-RW) is a critical mechanism that enables effective conditioning in ControlNet by adapting the strength of the guidance signal to the spatial resolution of each layer in the U-Net. Rather than applying a uniform scale to all residual injections, CFG-RW introduces a dynamic scheme:
\[ w_i = \frac {64}{h_i} \]
where \( w_i \) is the guidance weight applied at a layer with spatial height \( h_i \). This design is grounded in the hierarchical nature of the U-Net and the dynamics of the denoising process in diffusion models. The key to preserving the base model’s generative capabilities lies in regulating the influence of these residuals according to resolution.
- Low-resolution layers (e.g., \(8 \times 8\), \(16 \times 16\)) are responsible for encoding global structure—object positions, shapes, and scene layout. These layers benefit from strong guidance, as alignment at this scale is critical for conditioning to take effect. Hence, CFG-RW assigns large weights (e.g., \(w_i = 8\) for \(h_i = 8\)) to amplify the control signal.
- High-resolution layers (e.g., \(32 \times 32\), \(64 \times 64\)) refine textures, edges, and fine detail. Here, excessive guidance can distort or overwrite the pretrained model’s realistic priors. Small weights (e.g., \(w_i = 1\) for \(h_i = 64\)) preserve freedom for the U-Net to leverage its learned generative capacity.
Why It Works Diffusion models denoise from coarse to fine: early steps shape global semantics, while later ones refine textures. ControlNet injects conditioning through residuals at every U-Net layer, but applying a uniform strength across resolutions introduces issues:
- Too weak at low resolutions: Structural guidance is underutilized, leading to semantic drift.
- Too strong at high resolutions: Fine details are over-constrained, reducing realism.
Resolution-Aware Weighting (CFG-RW) resolves this by scaling the residual strength inversely with spatial resolution. This ensures: stronger guidance for layers encoding coarse structure, and softer influence where detail synthesis must remain flexible. Because the base U-Net is frozen, this modulation gently steers the generative process without destabilizing pretrained behavior.
Training Intuition With CFG-RW ControlNet is trained on a small paired dataset \((x, y)\), where \(x\) is the conditioning input and \(y\) the target image. The denoising objective remains unchanged, and only the ControlNet branch is updated. Residuals start with zero-initialized weights, ensuring that early training mimics the original model. As gradients accumulate, residuals learn to inject useful control, progressively modulated by CFG-RW to balance structure and detail. This setup enables stable finetuning while preserving generative fidelity.
In summary, the integration of CFG and the introduction of CFG-RW in ControlNet provide a nuanced mechanism for balancing condition adherence and image realism. By dynamically adjusting guidance strength across resolutions, ControlNet achieves high-quality, semantically aligned image generation, even when conditioned on complex inputs like edge maps or depth maps. This advancement underscores ControlNet’s robustness and versatility in controllable image synthesis. In the next part, we explore the limitations of ControlNet, motivating us towards following works.
Limitations of ControlNet and the Need for Semantic Conditioning ControlNet represents a major advance in controllable image synthesis. By introducing condition maps—such as Canny edges, human poses, or depth estimates—into a frozen diffusion model, it enables users to steer image generation with fine-grained structural constraints. However, it is important to emphasize a subtle but critical limitation: although ControlNet can be trained on full images, it cannot directly accept them as conditioning inputs. Instead, the image must be converted into a structural map—such as an edge sketch or depth projection—via a separate preprocessing pipeline.
This design choice is not arbitrary. The control branch in ControlNet is injected as residual guidance into a frozen U-Net, where each layer encodes spatially aligned features at different resolutions. To avoid interfering with the pretrained backbone, the injected condition must be spatially structured and semantically simple—matching the inductive biases of the U-Net. Raw RGB images are too entangled: they mix high-level semantics with textures, lighting, and style cues that do not map cleanly onto the diffusion model’s feature hierarchy. Structural maps, by contrast, are sparse, modality-aligned inputs that can guide early-stage generation without disrupting fine detail synthesis.
As a result, even when the training dataset contains full images, ControlNet learns to rely on their preprocessed structural representations. These projections are useful but inherently limited, as they discard much of the image’s global context.
Several limitations arise from this design:
- Brittle and domain-specific. The quality of condition maps depends on external models (e.g., edge detectors or depth estimators), which may fail on atypical, occluded, or stylized inputs.
- Workflow friction. Generating these maps adds overhead to the user pipeline, breaking the simplicity of prompting with raw images.
- Information bottleneck. Much of the source image’s richness—style, mood, identity—is lost when projecting it into a sparse or low-resolution structural format.
Lack of Semantic Awareness The core limitation of ControlNet is its inability to condition on high-level visual semantics:
- It cannot preserve or replicate an individual’s identity, since structure alone is insufficient to describe fine facial or bodily characteristics.
- It does not capture or transfer artistic style, which depends on texture, color, and abstraction—not just shape or layout.
- It cannot convey emotional tone or scene context, which emerge from the global gestalt of an image rather than any explicit structural map.
Limited Compositionality and Scalability While ControlNet supports combining multiple condition maps (e.g., pose + depth), doing so often requires separate parallel branches, each tied to its own preprocessor and parameter set. This introduces:
- Architectural complexity. Adding more conditions increases VRAM usage and inference latency.
- Signal conflict. Structural conditions may provide conflicting guidance (e.g., pose suggests one layout, depth another), requiring manual resolution or custom weighting schemes.
These shortcomings underscore a key insight: ControlNet excels at where things go, but not at what they are. It anchors generation to spatial constraints, but ignores the high-level visual semantics that define identity, style, and intent.
This motivates a new class of conditioning methods—those that allow users to guide generation using images themselves as prompts. Rather than reducing an image to its skeletal structure, these approaches aim to preserve and transfer the holistic content, mood, and semantics encoded in the image. One such solution, which we present next, is the IP-Adapter framework: a modular design for injecting semantic image features into pretrained diffusion models without retraining or disrupting text conditioning.
Enrichment 20.11.9: IP-Adapter — Semantic Image Prompting for DMs
Motivation and Background Text-to-image diffusion models, such as Stable Diffusion, have revolutionized the field of generative AI by producing high-fidelity images from textual descriptions. However, guiding these models to generate images that precisely match user intent can be challenging. Crafting effective prompts often involves intricate prompt engineering, where users must carefully phrase their descriptions to elicit specific visual attributes. Moreover, text alone may fall short in conveying complex scenes, abstract concepts, or nuanced styles, limiting the creative control available to users.
To address these limitations, incorporating image prompts emerges as a compelling alternative. The adage “a picture is worth a thousand words” aptly captures the value of visual cues in conveying detailed information. Image prompts can encapsulate intricate styles, specific identities, or subtle emotional tones that might be difficult to articulate through text alone. Early methods, such as DALL·E 2, introduced image prompting capabilities but often required extensive fine-tuning of the entire model, which was computationally intensive and risked compromising the model’s original text-to-image performance. More recent approaches, like ControlNet, have provided structural control by conditioning on explicit visual features such as edges, depth maps, or poses. However, these methods rely on external preprocessing and lack inherent semantic understanding of high-level concepts, and often fine-grained features we want to retain in the generation process.
Introducing IP-Adapter: A Lightweight and Compatible Solution IP-Adapter [733] provides a plug-and-play mechanism for adding image prompt conditioning to pretrained text-to-image diffusion models—without any modification to the U-Net itself. Instead of forcing image and text information through the same cross-attention heads—heads that were originally trained exclusively on text—the adapter introduces a decoupled pathway: one cross-attention block for the text prompt (frozen), and one for the image prompt (trainable), both attending to the same latent query features.
Imagine two expert interpreters:
- The original, frozen attention module is a linguist—precisely trained to interpret prompts like “a smiling woman in a red dress.”
- The adapter is an art critic—skilled in extracting pose, style, texture, and fine-grained visual cues from a reference image.
Both receive the same Query—a partial image undergoing denoising—and offer distinct “translations” (attention outputs). The fusion of these two outputs forms a single signal that guides the next denoising step.
Why IP-Adapter Works Without Compromising the Base Model
1. Image Guidance via Decoupled Cross-Attention in U-Net Blocks The U-Net architecture used in diffusion models contains multiple cross-attention blocks distributed along its downsampling and upsampling paths. Each of these blocks incorporates text conditioning by computing attention outputs using queries \( Q = Z W_q \), keys \( K = c_t W_k \), and values \( V = c_t W_v \), where \( Z \) is the U-Net’s internal latent activation, \( c_t \) is the text embedding, and the projection matrices \( W_q, W_k, W_v \) are frozen. The resulting attention output is: \[ Z' = \mbox{Attention}(Q, c_t W_k, c_t W_v). \]
IP-Adapter introduces a separate image-guided cross-attention module at each of these blocks. It operates on the same \( Q = Z W_q \) but uses independent, trainable projections \( W'_k, W'_v \) to attend to image features \( c_i \), computing: \[ Z'' = \mbox{Attention}(Q, c_i W'_k, c_i W'_v). \] This parallel path enables the adapter to extract and inject visual information—such as identity, style, or layout—without modifying or interfering with the pretrained text-conditioning weights.
2. The Base U-Net Remains Fully Frozen All components of the pretrained U-Net remain unchanged: convolutional layers, residual connections, normalization layers, and the text-based attention weights (\( W_q, W_k, W_v \)) are frozen across all attention blocks. The only trainable components are the new image-specific projections \( W'_k, W'_v \) and the lightweight image embedding projection head. Thus, the U-Net continues to perform noise prediction exactly as learned during pretraining. IP-Adapter merely enriches the context it receives, without altering its core computation.
3. Safe Integration via Additive Fusion To preserve structural compatibility, the image-based attention output \( Z'' \) is computed to match the shape of the existing text-conditioned context \( Z' \). The two are fused through an additive mechanism: \[ Z_{\mbox{new}} = Z' + \lambda \cdot Z'', \] where \( \lambda \in [0, 1] \) is a scalar hyperparameter set by the user before inference to control the influence of image conditioning. This formulation ensures that guidance from the adapter is smoothly integrated. When \( \lambda = 0 \), the model exactly reverts to its original behavior.
4. Denoising Logic is Preserved by Construction Because the U-Net is entirely frozen, no part of its denoising logic is overwritten or re-learned. During training, the adapter’s weights \( W'_k, W'_v \) are optimized to produce \( Z'' \) that complements \( Z' \) in minimizing the standard denoising loss. If \( Z'' \) introduces irrelevant or harmful information, the resulting loss penalizes this, driving the adapter to reduce \( Z'' \)—often to near-zero. Thus, the adapter either contributes helpful signal or defaults to silence, ensuring denoising is never degraded.
5. \(\lambda \) Offers Explicit, Safe, Inference-Time Control The scalar \( \lambda \) is not a learned parameter but a user-controlled value selected at inference time. It governs the contribution of \( Z'' \) as follows:
- \( \lambda = 0 \): the adapter is disabled; only \( Z' \) is used.
- \( \lambda = 1 \): full image guidance is applied via \( Z'' \).
- \( 0 < \lambda < 1 \): image and text context are blended in proportion.
Because \( \lambda \) scales the already trained \( Z'' \), it does not affect the underlying weights or the stability of the generation. This allows users to modulate the visual influence without retraining, enabling safe and interpretable control.
6. Summary: Why This Architecture is Effective and Non-Destructive IP-Adapter succeeds by introducing guidance precisely where U-Net models expect external context—within their cross-attention layers—while preserving all pretrained weights. Its effectiveness and safety arise from:
- Structural decoupling: text and image use separate attention paths.
- Frozen base model: all U-Net operations and weights remain unchanged.
- Additive fusion: \( Z'' \) is integrated without overwriting \( Z' \).
- Controlled training: the adapter is optimized to cooperate with a fixed base.
- User governance: \( \lambda \) determines adapter influence at inference.
Together, these principles exemplify the design philosophy of parameter-efficient fine-tuning (PEFT): adding new capabilities through small, modular changes, while ensuring reversibility, compatibility, and robustness. The adapter does not interfere with the base model—it collaborates with it. As a result, IP-Adapter provides powerful image guidance without compromising the original model’s generality or denoising quality.
ControlNet vs. IP-Adapter: Structural vs. Semantic Conditioning Both ControlNet and IP-Adapter extend text-to-image diffusion models by introducing additional conditioning mechanisms. However, they differ fundamentally in the type of information they interpret, how they integrate it into the U-Net, and the nature of control they exert over image generation.
ControlNet: Explicit Structural Conditioning ControlNet is designed to enforce spatial precision by conditioning the diffusion process on externally preprocessed structural maps.
- Input Modality: ControlNet operates on preprocessed control maps—such as Canny edges, OpenPose skeletons, or monocular depth maps—which distill raw images into sparse, low-dimensional spatial blueprints. These inputs encode layout and pose explicitly, providing a geometric scaffold for the generation process.
- Mechanism: The architecture introduces a trainable replica of the U-Net’s encoder and middle blocks. This auxiliary pathway processes the control map directly, acting as a specialized feature transformer that maps the structured signal into U-Net-compatible latent modifications. Its outputs are then fused into the original, frozen U-Net via zero-initialized \( 1 \times 1 \) convolutions, ensuring stable and gradual integration of the control signal during training.
-
Using a Pretrained ControlNet with Raw Images:
A common misunderstanding is that ControlNet, since it generates full-resolution images, should also accept raw images as control inputs. This confuses the output target of the diffusion model with the conditioning input to the control branch. ControlNet’s trainable modules are explicitly trained to interpret filtered, structured control maps—not raw photographs.
These control maps are highly reduced representations that isolate spatial features: for instance, an edge map contains only high-contrast contours, and a pose map contains sparse landmark joints. ControlNet’s learned filters are attuned to these simple, low-frequency patterns. Feeding in a raw image instead—rich in color, texture, illumination, and semantics—leads to a representational mismatch. The control branch expects structured geometry but receives entangled visual information instead. As a result, its activations become incoherent, and the injected guidance to the U-Net is noisy, leading to degraded or uncontrolled outputs.
-
Finetuning ControlNet on Raw Images (Without Adding an Encoder):
One might consider finetuning the existing ControlNet architecture using raw images as input instead of preprocessed control maps. However, this approach presents serious limitations: the control branch lacks the inductive bias or capacity to disentangle structure from raw pixels. Unlike semantic guidance models like IP-Adapter, it has no image encoder (e.g., CLIP) to process raw inputs into higher-level embeddings. It would be akin to retraining an architect to extract floor plans directly from artistic photographs without specialized tools. In practice, training such a system without architectural changes would likely result in poor convergence, highly inconsistent structural alignment, and a loss of controllability.
-
Training ControlNet with an Added Encoder:
To enable ControlNet to accept raw image inputs, one could prepend a pretrained visual encoder—such as CLIP, ViT, or ResNet—to its control branch. This encoder would transform the raw reference image into a semantic or structural embedding, which the control U-Net could then learn to decode into modulation signals for the diffusion backbone. Conceptually, this setup decomposes the control task into two stages:
- 1.
- Semantic or Structural Feature Extraction: The image encoder must extract useful structural or compositional signals (e.g., pose, depth, edge cues) from high-dimensional raw pixel data.
- 2.
- Conditional Feature Injection: The control U-Net must learn to map these features into latent-space modulations that steer the frozen U-Net’s denoising trajectory in a controlled manner.
While this is theoretically feasible, it is practically inefficient and undermines the original design motivations of ControlNet. Even when using a powerful pretrained encoder (like CLIP), the downstream control branch—a full copy of the U-Net’s encoder and middle blocks—must still be trained to convert the encoder’s outputs into usable control signals. This results in several drawbacks:
- Training Complexity: Despite freezing the encoder or initializing it from a strong checkpoint, the overall learning task remains complex. The control branch must learn to interpret potentially noisy or overcomplete embeddings from the encoder—without the benefit of explicit structural supervision. This makes convergence slower and less reliable than the current ControlNet approach, which uses clean, task-specific maps as input.
-
Data Demands: If the encoder is trained from scratch, the model becomes highly data-hungry. But even with a pretrained encoder, effective end-to-end finetuning often requires significant domain-specific tuning or adapter layers, especially if the encoder is not already aligned with the generation task.
- Architectural Inefficiency: The approach reintroduces the core inefficiency that IP-Adapter was designed to avoid: duplicating large parts of the U-Net architecture for every control type. In this case, a full U-Net control branch must still be trained and retained—even though the raw image input could have been handled more efficiently via lightweight cross-attention, as done in IP-Adapter.
- Loss of Interpretability and Control: Unlike preprocessed control maps (e.g., sketches, poses), raw-image embeddings are not human-editable. By relying on implicit structure extracted from raw inputs, this design sacrifices the explicit, modular control that makes ControlNet so appealing for tasks requiring fine spatial guidance.
In summary, ControlNet delivers precise spatial control by learning from explicit structural maps and avoids the burden of interpreting raw image complexity. Attempts to bypass preprocessing either lead to poor results (when used as-is) or impose heavy learning burdens (if rearchitected). This design tradeoff reflects ControlNet’s core strength: it is a structural controller, not a semantic interpreter.
The following figure showcases the versatility of IP-Adapter in integrating image prompts into text-to-image diffusion models. The central image in each example serves as the image prompt, providing semantic guidance for the generation process.
-
Right Column: Demonstrates applications where the image prompt is combined with textual prompts to achieve:
- Image Variation: Generating stylistic or thematic variations of the image prompt.
- Multimodal Generation: Merging semantic cues from both the image and text prompts to create novel compositions.
- Inpainting: Filling in missing or altered regions of the image while preserving its overall semantics.
-
Left Column: Illustrates scenarios where the image prompt is used alongside structural conditions (e.g., pose, depth maps) to enforce spatial constraints, enabling:
- Controllable Generation: Producing images that adhere to specific structural layouts while maintaining the semantic essence of the image prompt.
Key Architectural Components and Detailed Integration
- Image Encoder and Global Embedding: The reference image is processed using a frozen vision encoder—typically OpenCLIP-ViT-H/14—which outputs a single global embedding vector \( e_{\mbox{img}} \in \mathbb {R}^D \). This vector captures high-level visual semantics such as identity, global composition, and stylistic intent. Note that \( D \) (e.g., 1024 for ViT-H/14) typically differs from the internal dimension \( d \) of the U-Net’s cross-attention layers (e.g., 768 in Stable Diffusion 1.5). Thus, a transformation is needed to bridge this dimensional gap.
-
Projection to Visual Tokens (\( \phi \)): Since the U-Net expects a sequence of \( N \) key/value tokens, each of dimension \( d \), IP-Adapter introduces a lightweight, trainable projection network: \[ \phi \colon \mathbb {R}^D \rightarrow \mathbb {R}^{N \times d} \] which maps the global image embedding \( e_{\mbox{img}} \) into a sequence of \( N \) visual tokens: \[ [c_1, \ldots , c_N] = \phi (e_{\mbox{img}}), \quad \mbox{with } c_i \in \mathbb {R}^d. \]
- Why Use \( N > 1 \): Multiple visual tokens enable the model to attend separately to different latent attributes of the reference image—such as pose, color palette, facial features, or overall scene layout. This mirrors how textual prompts are split into subword tokens, each contributing distinct semantic signals. A typical choice is \( N = 4 \), balancing diversity of representation with computational efficiency.
-
Structure of \( \phi \): The projection network consists of a single linear layer followed by Layer Normalization: \[ \phi (e_{\mbox{img}}) = \mbox{LayerNorm}(W_\phi e_{\mbox{img}}), \quad \mbox{with } W_\phi \in \mathbb {R}^{(N \cdot d) \times D} \] The result is reshaped into a matrix in \( \mathbb {R}^{N \times d} \). The LayerNorm is applied across token dimensions and serves two key purposes:
- 1.
- Statistical stability: It normalizes the projected tokens, reducing internal covariate shift and promoting smoother gradient flow during training.
- 2.
- Architectural compatibility: It aligns the statistics of the visual tokens with those of the text encoder, which are also typically normalized. This facilitates better integration into the pretrained U-Net’s attention layers, which expect normalized key/value inputs.
-
Parallel Cross-Attention Layers: Let \( Z \in \mathbb {R}^{L \times d} \) denote the input query features from an intermediate U-Net block, and let \( c_t \in \mathbb {R}^{T \times d} \) be the tokenized text embeddings from the frozen CLIP text encoder. The original cross-attention mechanism in the pretrained U-Net computes:
\[ Z' = \mathrm {Attention}(Q, K, V) = \mathrm {Softmax}\left ( \frac {QK^\top }{\sqrt {d}} \right ) V, \] where \[ Q = Z W_q, \quad K = c_t W_k, \quad V = c_t W_v, \] and \( W_q, W_k, W_v \in \mathbb {R}^{d \times d} \) are the frozen projection matrices.
To introduce visual conditioning, IP-Adapter appends a decoupled image-specific attention stream using the same queries \( Q \), but separate keys and values derived from the projected image token sequence \( c_i \in \mathbb {R}^{N \times d} \): \[ Z'' = \mathrm {Attention}(Q, K', V') = \mathrm {Softmax}\left ( \frac {Q K'^\top }{\sqrt {d}} \right ) V', \] where \[ K' = c_i W'_k, \quad V' = c_i W'_v, \] and \( W'_k, W'_v \in \mathbb {R}^{d \times d} \) are new trainable projection matrices. These are typically initialized from \( W_k \) and \( W_v \) to accelerate training convergence.
- Fusion Strategy: The outputs of the text-guided and image-guided attention modules are combined additively: \[ Z_{\mbox{new}} = Z' + \lambda \cdot Z'', \] where \( \lambda \in \mathbb {R} \) is a tunable scalar controlling the influence of the image prompt. At inference time, adjusting \( \lambda \) allows for fine-grained control over the visual guidance: \( \lambda = 1 \) yields full conditioning on the image prompt, while \( \lambda = 0 \) recovers the original text-only generation behavior.
Versatility and Generalization without Fine-Tuning A key strength of the IP-Adapter architecture lies in its remarkable generalization and composability. Once trained, the adapter can be reused across a wide variety of downstream tasks without requiring any task-specific fine-tuning. It remains compatible with community models built upon the same base U-Net backbone (e.g., Stable Diffusion v1.5) and can be combined seamlessly with structured conditioning mechanisms such as ControlNet [773].
This flexibility is enabled by IP-Adapter’s non-invasive, modular design. Its decoupled attention layers are appended orthogonally to the pretrained U-Net, and its lightweight projection network transforms the reference image into a short sequence of visual tokens. These tokens serve as semantic key–value embeddings that are injected into the added image-specific attention stream. Because the architecture avoids modifying the backbone U-Net or interfering with the frozen text encoder, it remains interoperable with other conditioning systems that operate on different modalities.
For example, when paired with ControlNet, the model can synthesize images that respect both high-level semantic intent (from the image prompt) and low-level spatial structure (from edge maps, depth, or pose). The semantic tokens from IP-Adapter modulate subject identity, style, and appearance, while the structured control map—processed through a parallel ControlNet—anchors the generation to a target layout. These influences act concurrently: one guiding what should appear, the other guiding how and where it should appear.
As illustrated in Figure 20.124, this compositional capability allows users to generate coherent, high-fidelity outputs where appearance and structure are jointly controlled. The adapter generalizes across visual styles, domains, and control inputs with no need to retrain for specific downstream tasks. This makes it a practical and powerful tool in real-world creative workflows, where flexibility, reuse, and modularity are critical.
Comparative Evaluation Across Structural Control Tasks To further validate its adaptability and effectiveness, IP-Adapter was comprehensively benchmarked against a wide range of alternative methods across multiple structural generation tasks. These competing approaches span three major categories:
- Trained-from-scratch models, such as Open unCLIP [508], Kandinsky-2.1 [531], and Versatile Diffusion [717], which are optimized end-to-end for joint image-text alignment.
- Fine-tuned models, including SD Image Variations [587] and SD unCLIP [588], which adapt pretrained diffusion models for image prompt inputs via extensive retraining.
- Adapter-based solutions, such as the Style Adapter of T2I-Adapter [442], Uni-ControlNet’s global controller [792], SeeCoder [716], and variants of ControlNet [773] (e.g., ControlNet-Reference and ControlNet-Shuffle), which inject image conditioning in a modular fashion.
Unlike methods that require task-specific retraining or rely on dedicated control structures for each condition type, IP-Adapter achieves competitive or superior results using a single, unified architecture. It supports a wide range of conditioning tasks—such as edge-to-image translation, sketch-to-style synthesis, and pose-guided generation—without retraining for each setup.
Image-to-Image Translation, Inpainting, and Multimodal Prompting IP-Adapter’s inherent strength lies in its remarkable versatility: it enables a single architecture with fixed parameters to adapt seamlessly across diverse image generation paradigms [733]. This includes high-quality image-to-image translation, image inpainting, and multimodal prompting, where both image and text jointly guide the generation process.
For image-to-image translation, diffusion pipelines often adopt strategies like SDEdit [422], which leverage stochastic differential equations to perform controlled image editing. Instead of generating an image from pure noise, SDEdit begins with a real image and adds a calibrated amount of noise to partially erase its content. The resulting noised image is then denoised under new conditions—such as a modified prompt or altered guidance signals—enabling flexible and constrained editing.
Within this framework, IP-Adapter contributes as a semantic controller. The image prompt is passed through a frozen CLIP encoder and a projection module to extract a dense embedding representing the identity, style, and global appearance of the subject. These embeddings are injected into the U-Net via dedicated cross-attention layers, enriching the denoising trajectory with semantic cues. Crucially, the structural integrity of the original input is preserved, since the spatial information is derived directly from the partially noised source image, not from external conditioning modules like ControlNet. This allows IP-Adapter to achieve high-fidelity transformations—preserving fine-grained appearance details.
For inpainting, a related mechanism is used: a portion of the input image is masked and replaced with noise, and the diffusion model fills in the missing region during the denoising process. IP-Adapter enhances this process by injecting semantic guidance from the reference image prompt, ensuring that the inpainted content remains faithful to the original subject’s identity, lighting conditions, and stylistic attributes. This is particularly useful in creative tasks such as occlusion removal, selective editing, or visual reimagination, where both consistency and controllability are paramount.
The same IP-Adapter architecture also supports multimodal prompting, where both an image and a text prompt jointly influence generation. This enables fine-grained and compositional control: the image prompt preserves visual identity, style, and structural cues, while the text prompt modulates high-level semantics—such as adding new attributes, changing scene context, or modifying object categories. Unlike fully fine-tuned image prompt models, which often lose their text-to-image capability, IP-Adapter retains both modalities and allows users to balance their influence via the inference-time weight \( \lambda \).
The synergy between image and text inputs makes IP-Adapter highly suitable for personalized and controllable generation scenarios. As we will now see, IP-Adapter also outperforms several multimodal baselines in this setting.
Figure 20.128 provides qualitative comparisons with competing methods for multimodal image generation. The results show that IP-Adapter produces images that better preserve identity, maintain high visual quality, and more faithfully follow both text and image prompts compared to BLIP-Diffusion, T2I-Adapter, and Uni-ControlNet.
In the next part, we explore ablation studies that demonstrate how IP-Adapter’s core architectural choices—including decoupled attention and feature granularity—affect the quality and controllability of generations.
Ablation: Validating Architectural Design To assess the effectiveness of its key architectural decisions, the IP-Adapter paper includes a set of controlled ablation experiments. These studies highlight the contribution of the decoupled cross-attention mechanism and investigate the trade-offs between different feature representations used in the adapter.
Baseline Comparison: Simple Adapter without Decoupling
A natural baseline is to compare IP-Adapter against a simpler variant that
injects image features using the existing text cross-attention layers—without the
decoupled attention pathway. While this approach simplifies integration, it suffers
from feature entanglement and capacity conflict between modalities.
As shown in Figure 20.129, the simple adapter baseline often struggles to preserve subject identity and generates content that deviates from the image prompt. In contrast, IP-Adapter achieves high alignment with the source image, demonstrating the necessity of modality separation for accurate multimodal fusion.
Granularity of Image Representations: Global vs. Fine-Grained Tokens
A key design decision in IP-Adapter is the choice of granularity for representing the image prompt. By default, the adapter extracts a single global CLIP embedding from the reference image and projects it into a small sequence of visual tokens (typically \( N = 4 \)). These tokens are then injected into the U-Net’s cross-attention layers to guide generation. This setup provides a lightweight and expressive way to convey high-level semantics—such as identity, style, and layout—while remaining efficient and generalizable.
To investigate whether more detailed spatial alignment could be achieved, the IP-Adapter authors explored an alternative design that uses fine-grained visual tokens. Instead of relying solely on the global embedding, this variant extracts grid features from the penultimate layer of the frozen CLIP vision encoder. These grid features retain localized spatial information and are processed by a lightweight transformer query network, which learns to distill them into a sequence of 16 learnable visual tokens. These finer-grained tokens are then used in the same cross-attention mechanism, replacing the global-token projection.
Experimental Setup and Trade-offs: This variant was trained on the same dataset and evaluated under identical generation settings to allow fair comparison with the global-token version. The results, shown in the following figure, highlight a clear trade-off. The fine-grained configuration improves consistency with the reference image, particularly in background structures and subtle textures. However, it also tends to constrain the generative process more tightly, leading to reduced diversity across output samples. In contrast, the default global-token design offers a strong balance between semantic fidelity and output variation, making it better suited for general-purpose use.
Importantly, this limitation in diversity with fine-grained tokens can often be mitigated by adding complementary conditioning—such as text prompts or ControlNet structural maps—which help guide the generative process while restoring flexibility. In practice, the global-token configuration remains the preferred choice for most applications due to its simplicity, efficiency, and broader compatibility with multimodal workflows.
These ablation studies confirm that both the decoupled architecture and the choice of token granularity play critical roles in the model’s performance. The modularity of IP-Adapter allows these components to be tailored depending on the intended use—whether for faithful recreation, stylized adaptation, or diverse sampling.
Looking Forward A core motivation behind IP-Adapter was to disentangle heterogeneous modalities—specifically, to inject visual semantics directly via image embeddings rather than forcing them through the linguistic bottleneck of text encoders. This decoupling resolved key limitations in early diffusion pipelines, where all conditioning—even image-derived information—had to pass through shared cross-attention layers, often degrading fidelity and limiting semantic expressiveness. By introducing dedicated visual pathways that operate alongside the frozen U-Net, IP-Adapter preserved both the semantic richness of image prompts and the integrity of pre-trained text-to-image capabilities [733].
While this modular design proved highly effective for visual prompting, it was never meant to support fully compositional control across multiple modalities. As use cases grow more complex—demanding joint integration of reference appearance, structural layout, and descriptive language—the limitations of modularity become increasingly evident. Combining multiple modules (e.g., IP-Adapter for visual identity, ControlNet for edges or pose, and a separate module for text) introduces architectural overhead, modality-specific constraints, and potential conflicts between independently routed guidance signals. Each modality is still handled in isolation, with no mechanism for learning their mutual interactions or resolving contradictions.
This has sparked a broader shift toward unified conditioning frameworks—architectures designed to ingest and fuse all input modalities within a single attention-driven latent space. Rather than bolting on more specialized adapters, these frameworks are trained end-to-end on mixed-modality sequences, allowing them to learn how different types of guidance interact, reinforce, or compete.
A compelling example of this conceptual leap is Transfusion [809], which we examine next. Whereas IP-Adapter introduces decoupled cross-attention to avoid modality entanglement, Transfusion instead embraces entanglement through a shared modeling framework. It trains a single transformer to jointly model discrete text tokens and continuous image patches as part of a unified sequence, using shared self-attention and feedforward layers across modalities. This enables the model to perform both language modeling and diffusion denoising within the same architecture—dissolving the boundaries that modular adapters merely isolate.
By learning to align and synthesize multimodal signals within a single generative process, Transfusion opens the door to richer, more coherent compositionality and seamless modality interaction—without the overhead of managing separate modules. It represents the natural evolution of multimodal generation: not just retrofitting existing systems with external guidance, but rethinking the generative architecture itself from the ground up.
Enrichment 20.11.10: Transfusion: Unified Multimodal Generation
Motivation and Overview Generative models have reached state-of-the-art performance in individual modalities: large language models (LLMs) like GPT excel at producing coherent and contextually rich text, while diffusion-based models such as Stable Diffusion generate highly realistic images. However, building a unified generative system capable of seamlessly reasoning across both text and image modalities remains a significant challenge.
Existing approaches to multimodal generation typically fall into one of two categories:
- Discrete Tokenization of Images: Approaches like DALL·E [509] or Chameleon [398] quantize images into discrete visual tokens (e.g., via VQ-VAEs), allowing them to be modeled autoregressively like text. While effective, this discretization introduces information loss and reduces the fidelity of visual synthesis.
- Modular Pipelines: Methods such as IP-Adapter [733] or ControlNet [773] augment existing text-to-image diffusion models with auxiliary components that inject conditioning signals. While flexible, these grafted architectures often lack global coherence, require per-modality customization, and struggle with joint, end-to-end reasoning.
Such designs are often brittle, especially when dealing with interleaved inputs (e.g., text-image-text) or outputs requiring fine cross-modal consistency.
Transfusion [809] overcomes these limitations with a clean and elegant solution: a single, modality-agnostic transformer trained end-to-end to model mixed sequences of text and image content. Rather than building separate encoders or injecting one modality into another, Transfusion unifies both within a shared token stream and a shared network backbone. It achieves this via two key design principles:
- Shared Transformer Backbone: A single transformer with shared weights processes both text tokens and continuous image patch embeddings. This facilitates uniform attention over all elements in the sequence and supports tight cross-modal interactions.
- Dual Training Objectives: The model is jointly trained with a language modeling loss (for text) and a denoising diffusion loss (for image patches). The training procedure teaches the model to predict the next text token and remove noise from corrupted image tokens—both using the same architecture.
This unified formulation enables Transfusion to support a wide range of input-output formats with a single model:
- Text \(\rightarrow \) Image: Text-to-image generation.
- Image \(\rightarrow \) Text: Image captioning and visual understanding.
-
Mixed \(\rightarrow \) Mixed: One of the most compelling strengths of Transfusion is its ability to process and generate rich interleaved sequences of text and images. These tasks involve both multimodal inputs and multimodal outputs—handled in a unified transformer pipeline. Such capabilities are essential for:
-
Visual storytelling: Given a sequence of text snippets—such as narrative sentences, scene descriptions, or story fragments—the model generates a coherent visual story by producing aligned image segments after each text block. Conversely, it can also generate interleaved text commentary or narrative lines from a sequence of input images.
For example:
"A boy opens a mysterious book." <BOI> image_1 <EOI>
"A portal begins to glow on the wall." <BOI> image_2 <EOI>
"He steps through, entering a dreamlike jungle." <BOI> image_3 <EOI>Each element is contextually grounded in prior ones, and the sequence evolves in both text and image domains, preserving temporal and semantic coherence.
- Multimodal dialog: The model supports dynamic interactions where inputs and outputs alternate between text and images. For instance, a user may submit an image followed by a question, and the model replies with a mix of visual and textual responses—such as diagrams, sketches, or annotated outputs. This enables applications in tutoring, grounded question answering, and multimodal assistants.
-
Text-guided image editing and inpainting: Given an input image and a text instruction, the model directly generates a modified image that reflects the desired edit, without requiring separate control modules or manually designed conditioning maps:
"Replace the red car with a bicycle." <BOI> edited_image <EOI>
These scenarios are challenging for traditional diffusion models, and some scenarios are challenging to even adapter-augmented architectures (e.g., ControlNet [773], IP-Adapter [733]). Such modular systems often lack the flexibility to process arbitrary multimodal sequences or to maintain cross-modal consistency across multiple alternating steps of generation.
In contrast, Transfusion achieves this by treating text tokens and continuous image tokens as part of the same autoregressive token sequence. The model does not differentiate between modalities at the architectural level—only special delimiter tokens (e.g., <BOI> (Beginning of Image), <EOI> (End of Image)) indicate modality boundaries. All tokens are processed uniformly using shared transformer layers, and multimodal coherence is learned end-to-end via joint training with language modeling and diffusion objectives.
This design enables the model to naturally reason over long multimodal contexts, propagate dependencies across modality transitions, and generate semantically aligned outputs that respect both linguistic structure and visual consistency.
-
Architecture and Training Pipeline of Transfusion To understand the unified nature of Transfusion, we now examine its complete generative pipeline—starting from raw image and text inputs, proceeding through tokenization and transformer processing, and culminating in joint modality-specific losses. This breakdown serves as the foundation for later sections covering generation and editing capabilities.
Part 1: Image Tokenization Pipeline To enable seamless multimodal generation, Transfusion converts images into continuous, transformer-compatible tokens that can be interleaved with discrete text tokens. This process preserves the spatial structure and rich visual semantics of the input while allowing joint processing by a single transformer.
-
Spatial Encoding via Convolutional VAE: The input image \( x \in \mathbb {R}^{H \times W \times 3} \) is passed through a pretrained convolutional Variational Autoencoder (VAE) [292], which encodes it into a lower-resolution latent feature map. The encoder is composed of stacked convolutional layers that downsample the image by a factor of \( s \), producing two tensors: \[ \mu (x), \log \sigma ^2(x) \in \mathbb {R}^{H' \times W' \times d}, \quad \mbox{with} \quad H' = H/s, \, W' = W/s \] Each spatial location \( (i,j) \) corresponds to a receptive field in the original image and defines a diagonal Gaussian distribution: \[ q(z_{i,j} \mid x) = \mathcal {N}(z_{i,j} \mid \mu _{i,j}, \sigma _{i,j}^2 \cdot I_d) \] During VAE training, latent samples are drawn using the reparameterization trick: \[ z_{i,j} = \mu _{i,j} + \sigma _{i,j} \cdot \epsilon _{i,j}, \quad \epsilon _{i,j} \sim \mathcal {N}(0, I_d) \] The decoder then reconstructs the original image \( \hat {x} \approx x \). The loss combines a reconstruction objective with a KL divergence regularizer to promote a smooth latent space: \[ \mathcal {L}_{\mbox{VAE}} = \mathbb {E}_{q(z \mid x)} \left [ \| \hat {x} - x \|^2 \right ] + \beta \cdot \mathrm {KL}(q(z \mid x) \,\|\, p(z)) \]
During downstream use (e.g., tokenization in Transfusion), the VAE encoder is kept frozen and the sampling step is disabled. Instead, the deterministic mean \( z := \mu (x) \in \mathbb {R}^{H' \times W' \times d} \) is used as the spatially-structured latent representation. Each vector \( z_{i,j} \in \mathbb {R}^d \) serves as a dense, localized encoding of a specific region in the input image.
-
Patching Strategy for Tokenization: The latent tensor \( z \) is then transformed into a 1D sequence of patch-level embeddings using one of two methods:
- Linear Projection: The latent map is divided into non-overlapping \( k \times k \) spatial blocks, each containing \( k^2 \) adjacent vectors \( z_{i,j} \in \mathbb {R}^d \). Each block is flattened into a vector of shape \( k^2 \cdot d \), then passed through a linear layer that compresses it back to dimension \( d \). This method provides a direct, local embedding of visual content and is easy to implement, but it lacks contextual integration beyond each patch.
- U-Net-style Downsampling (Preferred): Alternatively, Transfusion applies a shallow convolutional encoder (often derived from the U-Net stem) to the full latent tensor \( z \). This module downsamples the spatial dimensions further (e.g., \( H' \to \tilde {H} \)), enabling each resulting token to summarize information over a broader receptive field. These richer embeddings are particularly beneficial for complex generation tasks that require high-level reasoning or long-range visual consistency.
- Token Sequence Construction: The resulting patch embeddings \( \{ z_1, \ldots , z_N \} \subset \mathbb {R}^d \) form a continuous image token sequence. These are either appended to or interleaved with discrete text tokens to form a unified input stream for the transformer. Special delimiter tokens (e.g., <BOI>, <EOI>) are inserted to mark modality boundaries, but the transformer processes all tokens jointly, enabling fluent multimodal generation and reasoning.
Part 2: Text Tokenization Pipeline The text prompt \(\mathcal {T}\) is first converted into a sequence of discrete tokens using a standard tokenizer, then embedded into the same feature space as the image tokens:
-
A Byte-Pair Encoding (BPE) tokenizer transforms the input string into a token sequence:
\[ \mathcal {T} \mapsto \{ w_1, w_2, \ldots , w_M \}, \quad w_i \in \mathcal {V}_{\mbox{text}} \]
-
Each token \(w_i\) is mapped to a continuous vector \(e_i \in \mathbb {R}^d\) using a learned embedding matrix \(E_{\mbox{text}} \in \mathbb {R}^{|\mathcal {V}_{\mbox{text}}| \times d}\):
\[ e_i = E_{\mbox{text}}[w_i] \]
-
This produces the text embedding sequence:
\[ x_{\mbox{text}} = [e_1, e_2, \ldots , e_M] \in \mathbb {R}^{M \times d} \]
Part 3: Multimodal Sequence Construction After obtaining both the image token sequence \(x_{\mbox{img}} = [z_1, z_2, \ldots , z_N] \in \mathbb {R}^{N \times d}\) from Part 1 and the text token embeddings \(x_{\mbox{text}} \in \mathbb {R}^{M \times d}\) from Part 2, Transfusion constructs a unified input sequence for the transformer.
-
Two special learnable embeddings are added to delimit the image region:
\[ e_{\texttt{<BOI>}}, \quad e_{\texttt{<EOI>}} \in \mathbb {R}^d \]
-
The final multimodal input to the transformer is the concatenation:
\[ x_{\mbox{input}} = [e_1, \ldots , e_M, e_{\texttt{<BOI>}}, z_1, \ldots , z_N, e_{\texttt{<EOI>}}] \in \mathbb {R}^{(M+N+2) \times d} \]
- Optional position encodings or segment embeddings may be added to indicate token roles and preserve modality structure.
Part 4: Transformer Processing with Hybrid Attention A single transformer autoregressively processes the multimodal sequence \(x_{\mbox{input}}\). To balance generation constraints with spatial reasoning, Transfusion adopts a hybrid attention mask:
- Causal attention is applied globally, ensuring that each token can only attend to previous tokens in the sequence.
- Bidirectional attention is enabled locally within the image region delimited by <BOI> and <EOI>, allowing all image tokens to attend to one another.
This hybrid masking strategy preserves autoregressive generation for the full sequence while enabling richer spatial reasoning among image tokens—improving sample fidelity and multimodal alignment.
Part 5: Training Objectives and Loss Functions Transfusion jointly optimizes a unified transformer model over both text and image inputs. The training procedure integrates two complementary objectives—autoregressive language modeling and latent-space denoising—applied respectively to text tokens and VAE image patches. These objectives are optimized simultaneously using shared model parameters, with losses computed over the appropriate modality regions in the input sequence.
-
Text Modeling Loss \(\mathcal {L}_{\mbox{text}}\): For positions in the sequence corresponding to text tokens \(\{ w_1, \ldots , w_M \}\), the model is trained to predict each next token \(w_{i+1}\) based on the preceding context \(w_{\leq i}\), using standard autoregressive language modeling.
\[ \mathcal {L}_{\mbox{text}} = - \sum _{i=1}^{M} \log p(w_{i+1} \mid w_{\leq i}) \]
The prediction is compared against the ground truth token from the training data, and the loss is computed as cross-entropy between the predicted distribution and the true next-token index. This formulation ensures that the model learns to generate fluent, contextually appropriate text conditioned on both prior tokens and (when available) image content.
-
Image Denoising Loss \(\mathcal {L}_{\mbox{diff}}\): For image regions—i.e., the continuous sequence of tokens \(z_0 \in \mathbb {R}^{N \times d}\) obtained by encoding and optionally downsampling the image with a pretrained VAE—the model is trained using a DDPM-style denoising objective.
During training, a timestep \(t \sim \{1, \ldots , T\}\) is sampled, and Gaussian noise is added to each image token \(z_0^{(j)} \in \mathbb {R}^d\) using the forward diffusion process:
\[ z_t^{(j)} = \sqrt {\bar {\alpha }_t} \, z_0^{(j)} + \sqrt {1 - \bar {\alpha }_t} \, \epsilon ^{(j)}, \quad \epsilon ^{(j)} \sim \mathcal {N}(0, I) \]
Here, \(\bar {\alpha }_t\) is a cumulative noise schedule, and \(\epsilon ^{(j)}\) is the sampled noise used to corrupt patch \(j\). The model is trained to predict \(\epsilon ^{(j)}\) from \(z_t^{(j)}\) and the timestep \(t\), minimizing the mean squared error over all patches:
\[ \mathcal {L}_{\mbox{diff}} = \mathbb {E}_{t, z_0, \epsilon } \left [ \frac {1}{N} \sum _{j=1}^{N} \left \| \epsilon _\theta (z_t^{(j)}, t) - \epsilon ^{(j)} \right \|_2^2 \right ] \]
This loss operates entirely in latent space; no decoding to pixels is performed during training. The ground truth for each position is the actual noise added in the forward process. The use of VAE latents enables spatial preservation and compact representation, making the diffusion process more efficient than pixel-level alternatives.
-
Total Training Loss \(\mathcal {L}_{\mbox{total}}\): The overall training objective combines both modality-specific terms into a weighted sum:
\[ \mathcal {L}_{\mbox{total}} = \lambda _{\mbox{text}} \cdot \mathcal {L}_{\mbox{text}} + \lambda _{\mbox{diff}} \cdot \mathcal {L}_{\mbox{diff}} \]
where \(\lambda _{\mbox{text}}, \lambda _{\mbox{diff}} \in \mathbb {R}_{\geq 0}\) are scalar coefficients that control the relative contribution of text modeling and image denoising to the final loss. In practice, the original Transfusion paper reports using \(\lambda _{\mbox{diff}} = 5\), giving higher weight to the image denoising component due to its higher dynamic range and training complexity.
Part 6: Key Advantages of the Training Design
- Full parameter sharing: No modality-specific blocks; language and vision share all layers.
- End-to-end joint training: All gradients flow through shared transformer, improving alignment.
- No discrete quantization: Image patches remain continuous, avoiding codebook collapse or token artifacts.
- Multimodal generation in a single pass: A single forward pass can generate image and text jointly.
Empirical Results and Qualitative Examples
Showcase: High-Quality Multi-Modal Generation One of the most compelling outcomes of the Transfusion model is its ability to generate high-fidelity, semantically grounded images from a wide range of compositional text prompts. Trained with 7B parameters on a dataset of 2 trillion multimodal tokens—including both text and images—the model produces coherent and visually expressive outputs that exhibit stylistic nuance, spatial awareness, and fine-grained linguistic alignment.
These qualitative results demonstrate not only stylistic diversity but also compositional understanding—a hallmark of strong multimodal reasoning. Unlike U-NET based diffusion architectures that rely on external encoders or modality-specific adapters, Transfusion achieves this performance using a single, unified transformer trained from scratch, without separate alignment stages or handcrafted prompt tuning.
Zero-Shot Image Editing via Fine-Tuning Beyond text-to-image synthesis, Transfusion also generalizes to the task of image editing through lightweight fine-tuning. A version of the 7B model was adapted on a dataset of only 8,000 image–text pairs, each consisting of an input image and a natural-language instruction describing a desired change (e.g., “Remove the cupcake on the plate” or “Change the tomato on the right to a green olive”).
This result is notable: without requiring any architectural changes—such as inpainting masks or diffusion-specific guidance—the model learns to apply textual edit instructions directly. Training is end-to-end, and the only modification is through supervised adaptation on the editing dataset. This demonstrates the expressive capacity of the underlying sequence model and suggests extensibility to broader tasks such as viewpoint manipulation, object insertion, or multimodal storytelling.
Ablation Studies and Experimental Insights To evaluate the core design choices of Transfusion [798], the authors conduct extensive ablations over attention masking, patch size, encoder/decoder type, noise scheduling and model scale. Both vision and language benchmarks are reported with the metrics below.
Interpreting Evaluation Metrics
- PPL (Perplexity) \(\downarrow \): Measures uncertainty in language modeling. Lower values correspond to better next-token prediction performance.
- Accuracy (Acc) \(\uparrow \): Multiple-choice question answering accuracy, especially on LLaMA-style QA tasks.
- CIDEr \(\uparrow \): A captioning metric measuring consensus with human-written references, widely used in MS-COCO.
- FID (Fréchet Inception Distance) \(\downarrow \): Evaluates the visual realism of generated images. Lower is better. See Section 20.5.2.0 for a detailed explanation.
- CLIP Score \(\uparrow \): Measures semantic alignment between generated image and caption using pretrained CLIP embeddings [498].
Attention Masking: Causal vs. Bidirectional Bidirectional self-attention applied within each image notably improves FID for linear encoders (\(61.3\!\to \!20.3\)); U-Nets also benefit, though to a lesser extent.
| Encoder/Dec. | Attention | C4 PPL | Wiki PPL | Acc | CIDEr | FID | CLIP |
| Linear | Causal | 10.4 | 6.0 | 51.4 | 12.7 | 61.3 | 23.0 |
| Linear | Bidirectional | 10.4 | 6.0 | 51.7 | 16.0 | 20.3 | 24.0 |
| U-Net | Causal | 10.3 | 5.9 | 52.0 | 23.3 | 16.8 | 25.3 |
| U-Net | Bidirectional | 10.3 | 5.9 | 51.9 | 25.4 | 16.7 | 25.4 |
Patch Size Variations Larger patches reduce token length and compute, but can hurt performance. U-Nets are more robust than linear encoders.
| Encoder/Dec. | Patch | C4 PPL | Wiki PPL | Acc | CIDEr | FID | CLIP |
| Linear | \(1\times 1\) (1024) | 10.3 | 5.9 | 52.2 | 12.0 | 21.0 | 24.0 |
| Linear | \(2\times 2\) (256) | 10.4 | 6.0 | 51.7 | 16.0 | 20.3 | 24.0 |
| Linear | \(4\times 4\) (64) | 10.9 | 6.3 | 49.8 | 14.3 | 25.6 | 22.6 |
| Linear | \(8\times 8\) (16) | 11.7 | 6.9 | 47.7 | 11.3 | 43.5 | 18.9 |
| U-Net | \(2\times 2\) (256) | 10.3 | 5.9 | 51.9 | 25.4 | 16.7 | 25.4 |
| U-Net | \(4\times 4\) (64) | 10.7 | 6.2 | 50.7 | 29.9 | 16.0 | 25.7 |
| U-Net | \(8\times 8\) (16) | 11.4 | 6.6 | 49.2 | 29.5 | 16.1 | 25.2 |
Encoding Architecture: Linear vs. U-Net U-Nets outperform linear encoders across model sizes with only a modest parameter increase.
| Params | Encoder | C4 PPL | Wiki PPL | Acc | CIDEr | FID | CLIP |
| 0.76 B | Linear | 10.4 | 6.0 | 51.7 | 16.0 | 20.3 | 24.0 |
| U-Net | 10.3 | 5.9 | 51.9 | 25.4 | 16.7 | 25.4 | |
| 7.0 B | Linear | 7.7 | 4.3 | 61.5 | 27.2 | 18.6 | 25.9 |
| U-Net | 7.8 | 4.3 | 61.1 | 33.7 | 16.0 | 26.5 |
Noise Scheduling in Image-to-Text Training Capping diffusion noise to timesteps \(t\le 500\) improves CIDEr without degrading other metrics.
| Model | Cap \(t\le 500\) | C4 PPL | Wiki PPL | Acc | CIDEr | FID |
| 0.76 B | ✗ | 10.3 | 5.9 | 51.9 | 25.4 | 16.7 |
| 0.76 B | ✓ | 10.3 | 5.9 | 52.1 | 29.4 | 16.5 |
| 7.0 B | ✗ | 7.8 | 4.3 | 61.1 | 33.7 | 16.0 |
| 7.0 B | ✓ | 7.7 | 4.3 | 60.9 | 35.2 | 15.7 |
Comparison to Specialized Generative Models A single Transfusion model achieves strong performance on both image and text tasks compared with state-of-the-art specialised models.
| Model | Params | COCO FID\(\downarrow \) | GenEval\(\uparrow \) | Acc\(\uparrow \) | Modality | Notes |
| SDXL [482] | 3.4 B | 6.66 | 0.55 | – | Image | Frozen encoder |
| DeepFloyd IF [612] | 10.2 B | 6.66 | 0.61 | – | Image | Cascaded diffusion |
| SD3 [149] | 12.7 B | – | 0.68 | – | Image | Synthetic caps |
| Chameleon [810] | 7.0 B | 26.7 | 0.39 | 67.1 | Multi | Discrete fusion |
| Transfusion [798] | 7.3 B | 6.78 | 0.63 | 66.1 | Multi | Unified LM + diffusion |
Summary The ablation findings from [798] provide a clear picture of what makes Transfusion effective: bidirectional intra-image attention is key to spatial coherence; U-Net-based patch encoders contribute strong inductive biases that enhance both fidelity and alignment; and careful tuning of patch size and noise scheduling enables efficient training without compromising performance. The success of this architecture demonstrates that unifying text and image processing under a shared transformer with continuous embeddings is not only feasible but highly performant.
At the same time, the reliance on continuous image tokens and diffusion-based generation introduces additional training and sampling complexity. This raises a natural question: can we achieve the benefits of modality unification using simpler, fully discrete generation schemes? In the following section, we explore such a possibility through the lens of the VAR framework, which revisits token-level autoregressive modeling for unified image and text generation—offering a different perspective on multimodal generative design.
Enrichment 20.11.11: Visual Autoregressive Modeling (VAR)
Traditional autoregressive (AR) models, such as PixelCNN or transformer-based image generators, generate images sequentially by predicting each token (pixel, patch, or VQ code) in a predefined raster scan order—typically left to right and top to bottom. While conceptually straightforward, this strategy is fundamentally at odds with the two-dimensional nature of images and the hierarchical way humans perceive visual content.
Visual Autoregressive Modeling (VAR) [615] reconsiders how autoregression should operate in the image domain. Instead of modeling a 2D grid as a flattened 1D sequence, VAR predicts image content in a coarse-to-fine, multi-scale manner. At each scale, the model generates an entire token map in parallel, then conditions the next higher-resolution prediction on this coarser output. This process mirrors how humans often process visual inputs: first recognizing global structure, then refining local details.
This approach leads to multiple benefits:
- Improved efficiency: Tokens at a given resolution are predicted in parallel, which drastically reduces the number of autoregressive steps compared to raster-scan generation.
- Higher fidelity: Coarse-to-fine guidance encourages global coherence and fine-grained detail simultaneously.
- Scalable modeling: VAR exhibits smooth scaling behavior similar to language transformers, showing predictable gains as model and compute increase.
As we now explore, this paradigm shift from token-wise raster autoregression to scale-wise parallel prediction yields state-of-the-art results on ImageNet and opens the door to efficient, high-fidelity generation pipelines.
Multi-Scale Architecture for Coarse-to-Fine Generation: How VAR Works The core contribution of Visual Autoregressive Modeling (VAR) [615] is a paradigm shift in how autoregressive models approach image generation. Instead of predicting tokens in a strict raster-scan order—row-by-row, left to right—VAR proposes a coarse-to-fine, scale-based generation strategy that better reflects how humans compose images: beginning with global structure and refining toward detail. This section explains the architecture and training pipeline, focusing on the two foundational stages: hierarchical tokenization and scale-aware prediction.
Overview: A Two-Stage Pipeline for Image Generation The Visual AutoRegressive (VAR) model [615] tackles the problem of high-fidelity image generation using a modular, two-stage approach:
- Stage 1: Multi-Scale VQ-VAE for Hierarchical Tokenization Transforms a continuous image into a hierarchy of discrete tokens, each representing visual content at a different scale (from global layout to local texture). This compresses the image into symbolic representations that are more structured and compact than pixels or raw latent features.
- Stage 2: Scale-Aware Autoregressive Transformer Learns to model the joint distribution of token hierarchies and to autoregressively generate image tokens from coarse to fine, either unconditionally or conditioned on class/text input. This allows realistic, structured image synthesis without generating pixels directly.
These two stages are trained separately and serve complementary purposes:
- The VQ-VAE (Stage 1) learns how to discretize an image into multi-scale tokens \( R = (r_1, \dots , r_K) \) and how to reconstruct the image from them.
- The transformer (Stage 2) learns how to generate realistic sequences of these tokens, modeling \( p(r_1, \dots , r_K \mid s) \) where \( s \) is an optional conditioning signal.
This design addresses key challenges in autoregressive image modeling:
- It avoids operating over raw pixels, which are high-dimensional and redundant.
- It introduces scale-level causality, so image generation proceeds hierarchically (not raster-scan), yielding better spatial inductive structure.
- It separates representation learning (handled by the VQ-VAE) from generation (handled by the transformer), simplifying optimization and improving sample quality.
We now explain each stage in detail, beginning with the multi-scale encoding process of the VQ-VAE.
Stage 1: Multi-Scale VQ-VAE for Hierarchical Tokenization The first stage of the VAR pipeline [615] transforms a continuous image into a set of discrete token maps across multiple resolutions. This step establishes a symbolic vocabulary over images, enabling a transformer in the second stage to model image generation as autoregressive token prediction. Prior works like DALL·E 1 [509] relied on a single-scale VQ-VAE, which forced each token to simultaneously capture high-level layout and low-level texture—often leading to trade-offs in expressivity. VAR overcomes this limitation through a hierarchical decomposition: \[ \mathbf {R} = (\mathbf {r}_1, \mathbf {r}_2, \dots , \mathbf {r}_K) \] where each token map \( \mathbf {r}_k \in \{0, \dots , V{-}1\}^{h_k \times w_k} \) encodes the image at scale \( k \), from coarse to fine. The hierarchy is constructed through residual refinement, ensuring that each level captures only the visual details not already modeled by coarser layers.
Hierarchical Token Encoding via Residual Refinement Let \( \mathbf {x} \in \mathbb {R}^{H \times W \times 3} \) be the input image. A shared convolutional encoder \( \mathbf {E} \) processes \( \mathbf {x} \) into a latent feature map: \[ \mathbf {f} \in \mathbb {R}^{H' \times W' \times C} \] where \( H' \ll H \), \( W' \ll W \), and \( C \) is the channel dimension. This map retains semantic structure while reducing spatial complexity.
To tokenize this image across multiple levels, the model applies a sequence of residual refinements. For each scale \( k \in \{1, \dots , K\} \), the following steps are executed:
- 1.
- Resolution Adaptation: Interpolate the latent map \( \mathbf {f} \) to resolution \( h_k \times w_k \), yielding a coarsened view appropriate for scale \( k \).
- 2.
- Discrete Quantization: Map the interpolated features to a discrete token map \( \mathbf {r}_k \in \{0, \dots , V{-}1\}^{h_k \times w_k} \) by finding the nearest entries in a shared codebook \( \mathbf {Z} \in \mathbb {R}^{V \times d} \). Each index corresponds to the closest code vector in \( \mathbf {Z} \), representing the local content at that location.
- 3.
- Code Vector Lookup: Retrieve the continuous code vectors associated with \( \mathbf {r}_k \), forming: \[ \mathbf {z}_k = \mathbf {Z}[\mathbf {r}_k] \in \mathbb {R}^{h_k \times w_k \times d} \]
- 4.
- Residual Update: Interpolate \( \mathbf {z}_k \) to the full resolution \( H' \times W' \), apply a scale-specific 1×1 convolution \( \phi _k \), and subtract the result from the shared latent: \[ \mathbf {f} \leftarrow \mathbf {f} - \phi _k\left (\mbox{Interpolate}(\mathbf {z}_k)\right ) \] This subtraction removes the information already modeled by level \( k \), forcing subsequent levels to focus on the residual detail. The subtraction step is critical: it decorrelates token maps across scales and ensures that each scale contributes new, non-overlapping information.
After completing this procedure for all \( K \) levels, the image is represented as a hierarchy of discrete symbolic tokens \( \mathbf {r}_1, \dots , \mathbf {r}_K \), suitable for autoregressive modeling.
Token Decoding and Image Reconstruction Given a full hierarchy of token maps \( (\mathbf {r}_1, \dots , \mathbf {r}_K) \), the decoder reconstructs the image by reversing the residual refinement process:
- 1.
- Embedding Recovery: Use the codebook \( \mathbf {Z} \) to retrieve continuous embeddings: \[ \mathbf {z}_k = \mathbf {Z}[\mathbf {r}_k] \in \mathbb {R}^{h_k \times w_k \times d} \]
- 2.
- Latent Aggregation: Interpolate each \( \mathbf {z}_k \) to resolution \( H' \times W' \), apply its convolution \( \phi _k \), and sum the results to reconstruct the latent feature map: \[ \hat {\mathbf {f}} = \sum _{k=1}^{K} \phi _k\left ( \mbox{Interpolate}(\mathbf {z}_k) \right ) \]
- 3.
- Image Synthesis: A lightweight convolutional decoder \( \mathbf {D} \) maps \( \hat {\mathbf {f}} \) to a reconstructed image: \[ \hat {\mathbf {x}} = \mathbf {D}(\hat {\mathbf {f}}) \in \mathbb {R}^{H \times W \times 3} \]
This decoding path exactly mirrors the refinement steps in reverse, enabling the discrete token maps to be faithfully converted back into high-resolution images.
Training Objective for the VQ-VAE The encoder–decoder pipeline is trained independently from the transformer using a perceptually aligned loss: \[ \mathcal {L}_{\mbox{VQ-VAE}} = \|\mathbf {x} - \hat {\mathbf {x}}\|_2 + \|\mathbf {f} - \hat {\mathbf {f}}\|_2 + \lambda _P \mathcal {L}_P(\hat {\mathbf {x}}) + \lambda _G \mathcal {L}_G(\hat {\mathbf {x}}) \] where:
- \( \|\mathbf {x} - \hat {\mathbf {x}}\|_2 \): Pixel-space L2 reconstruction loss
- \( \|\mathbf {f} - \hat {\mathbf {f}}\|_2 \): Latent-space consistency loss
- \( \mathcal {L}_P(\hat {\mathbf {x}}) \): Perceptual loss (e.g., LPIPS) weighted by \( \lambda _P \)
- \( \mathcal {L}_G(\hat {\mathbf {x}}) \): Adversarial loss weighted by \( \lambda _G \)
This compound objective encourages both structural accuracy and perceptual realism in the reconstructed images. Once trained, the VQ-VAE becomes a symbolic bridge between continuous images and the transformer in Stage 2.
Stage 2: Scale-Aware Autoregressive Transformer While Stage 1 defines how to tokenize and reconstruct an image using a hierarchy of discrete visual codes, Stage 2 transforms this representation into a full generative model. The transformer introduced here is trained to model the joint probability distribution over multi-scale token maps produced by the VQ-VAE. Its objective is to generate a sequence of token maps that are semantically coherent and hierarchically consistent—ultimately producing realistic images when decoded by Stage 1.
\[ p(\mathbf {r}_1, \dots , \mathbf {r}_K \mid \mathbf {s}) \]
Here, \( \mathbf {s} \) is an optional conditioning signal such as a class label or text prompt, and \( \mathbf {r}_k \in \mathbb {Z}^{h_k \times w_k} \) denotes the token map at scale \( k \).
From Tokens to Embeddings: Transformer Inputs The transformer does not operate directly on the discrete token indices \( \mathbf {r}_k \). Instead, each token map \( \mathbf {r}_k \) is transformed into a continuous embedding map \( \mathbf {e}_k \in \mathbb {R}^{h_k \times w_k \times D_{\mbox{model}}} \) through the following procedure:
- 1.
- Codebook Lookup: Each integer token index in \( \mathbf {r}_k \) is used to retrieve its associated code vector from the shared codebook \( \mathbf {Z} \in \mathbb {R}^{V \times d} \), forming a spatial map \( \mathbf {z}_k = \mathbf {Z}[\mathbf {r}_k] \in \mathbb {R}^{h_k \times w_k \times d} \).
- 2.
- Projection to Transformer Dimension: The code vectors \( \mathbf {z}_k \) are projected to the transformer’s model dimension \( D_{\mbox{model}} \) via a learned linear layer.
- 3.
- Positional and Scale Embedding: Positional embeddings are added to encode spatial location within the grid, and a scale-specific embedding is added to indicate the resolution level \( k \). The resulting map is denoted \( \mathbf {e}_k \), and it serves as the input to the transformer for scale \( k \).
Similarly, the conditioning signal \( \mathbf {s} \) is embedded as \( \mathbf {s}_{\mbox{emb}} \in \mathbb {R}^{D_{\mbox{model}}} \). Together, the input to the transformer at training time is the sequence:
\[ \left [ \mathbf {s}_{\mbox{emb}}, \mathbf {e}_1, \dots , \mathbf {e}_{K-1} \right ] \]
Why a Second Stage is Needed This two-stage setup reflects a deliberate separation of concerns:
- Stage 1 (VQ-VAE): Encodes perceptual realism, spatial consistency, and image fidelity via hierarchical quantization and reconstruction.
- Stage 2 (Transformer): Focuses purely on symbolic generation—learning to synthesize plausible token sequences that form coherent, multi-scale image structures.
This design allows the transformer to reason over a compact, expressive, and semantically meaningful representation space, without being burdened by low-level texture synthesis.
Autoregressive Modeling Across Scales Unlike pixel-level autoregressive models (e.g., PixelRNN) that model:
\[ p(\mathbf {x}) = \prod _{i=1}^{H \cdot W} p(x_i \mid x_{<i}), \]
the VAR transformer performs next-scale prediction, modeling causality across hierarchical levels:
\[ p(\mathbf {r}_1, \dots , \mathbf {r}_K \mid \mathbf {s}) = \prod _{k=1}^{K} p(\mathbf {r}_k \mid \mathbf {s}, \mathbf {r}_{<k}). \]
That is, the model generates each token map \( \mathbf {r}_k \) in parallel across spatial locations, but strictly conditioned on previously generated scales and the conditioning input. Internally, this corresponds to processing the sequence:
\[ \left [ \mathbf {s}_{\mbox{emb}}, \mathbf {e}_1, \dots , \mathbf {e}_{K-1} \right ] \longrightarrow \mbox{predict } \mathbf {r}_K. \]
To ensure this behavior, a blockwise causal attention mask is applied within the transformer. This mask enforces the following:
-
Tokens at scale \( k \) may attend to:
- The conditioning embedding \( \mathbf {s}_{\mbox{emb}} \)
- All embedded tokens from previous scales \( \mathbf {e}_1, \dots , \mathbf {e}_{k-1} \)
-
Tokens at scale \( k \) cannot attend to:
- Other tokens within \( \mathbf {e}_k \)
- Tokens from future scales \( \mathbf {e}_{>k} \)
This yields a well-defined autoregressive ordering across resolution levels, while enabling parallel token prediction within each scale.
Training Procedure The model is trained to maximize the log-likelihood of the token maps across all scales:
\[ \mathcal {L}_{\mbox{AR}} = -\sum _{k=1}^{K} \sum _{i=1}^{h_k \cdot w_k} \log p\left (\mathbf {r}_{k,i}^{\mbox{gt}} \mid \mathbf {s}_{\mbox{emb}}, \mathbf {e}_1, \dots , \mathbf {e}_{k-1}\right ), \]
where \( \mathbf {r}_{k,i}^{\mbox{gt}} \) is the ground-truth token index at spatial position \( i \) in scale \( k \), and \( p(\cdot ) \) is the predicted probability distribution over the codebook vocabulary. The transformer outputs a distribution for each token position, and the cross-entropy loss is applied at every location.
Importantly, no teacher forcing is applied within a scale. When predicting \( \mathbf {r}_k \), the model is not conditioned on ground-truth tokens within that map—only on previously predicted scales. This enables efficient training with strong inductive bias toward scale-level compositionality.
Inference and Generation Generation proceeds autoregressively over scales using the same principle:
- 1.
- Predict \( \hat {\mathbf {r}}_1 \sim p(\cdot \mid \mathbf {s}_{\mbox{emb}}) \)
- 2.
- Embed \( \hat {\mathbf {r}}_1 \rightarrow \mathbf {e}_1 \)
- 3.
- Predict \( \hat {\mathbf {r}}_2 \sim p(\cdot \mid \mathbf {s}_{\mbox{emb}}, \mathbf {e}_1) \)
- 4.
- Embed \( \hat {\mathbf {r}}_2 \rightarrow \mathbf {e}_2 \), and so on.
Each prediction is performed in parallel across spatial locations, making inference much faster than raster-scan approaches. Key-value (KV) caching is applied to preserve and reuse the attention states of \( \mathbf {s}_{\mbox{emb}}, \mathbf {e}_1, \dots , \mathbf {e}_{k-1} \), avoiding recomputation in deep transformers.
Final Decoding and Image Reconstruction After generating the full sequence \( \hat {\mathbf {r}}_1, \dots , \hat {\mathbf {r}}_K \), the decoder reconstructs the image as in Stage 1:
- 1.
- For each \( \hat {\mathbf {r}}_k \), lookup code vectors from the codebook: \( \hat {\mathbf {z}}_k = \mathbf {Z}[\hat {\mathbf {r}}_k] \)
- 2.
- Interpolate each \( \hat {\mathbf {z}}_k \) to resolution \( h_K \times w_K \)
- 3.
- Filter with scale-specific convolution \( \phi _k \)
- 4.
- Sum to form the latent map: \[ \hat {\mathbf {f}} = \sum _{k=1}^{K} \phi _k\left ( \mbox{Interpolate}(\hat {\mathbf {z}}_k) \right ) \]
- 5.
- Decode to full-resolution image: \[ \hat {\mathbf {x}} = \mathbf {D}(\hat {\mathbf {f}}) \]
This completes the symbolic-to-visual generation pipeline. The transformer produces discrete codes that encode visual semantics and layout, while the VQ-VAE decoder renders them into photorealistic images.
Benefits of the VAR Design VAR’s architecture offers several advantages:
- 1.
- Spatial locality is preserved, avoiding the unnatural 1D flattening of images.
- 2.
- Inference is parallelized within each resolution, enabling fast generation.
- 3.
- Global structure is conditioned into finer details via multi-scale refinement.
- 4.
- Transformer capacity is efficiently used, since each level focuses on simpler sub-distributions.
Experimental Results: High-Quality Generation and Editing After training both the multi-scale VQ-VAE and the scale-aware transformer, the VAR model [615] demonstrates compelling performance across a range of image generation tasks. Notably, it achieves high visual fidelity on ImageNet [118] at resolutions up to \(512 \times 512\), and supports zero-shot editing — despite being trained with only unconditional or class-conditional supervision.
Generation Quality. VAR achieves state-of-the-art sample quality on the ImageNet-256 and ImageNet-512 benchmarks. Visually, its samples are both semantically rich and globally coherent — showcasing correct object structure, texture, and style. This is due to its coarse-to-fine generation mechanism: the transformer first predicts low-resolution structural layout via coarse token maps, then refines texture and details in subsequent finer maps, guided by the VQ-VAE decoder.
Zero-Shot Editing. The ability to modify image content without additional supervision is enabled by the discrete tokenization of the VQ-VAE and the structured generative pathway. In the bottom row of Figure 20.138, input images are embedded into VAR’s token space and selectively altered before decoding — showcasing realistic object transformations, viewpoint changes, and fine-grained edits, all without retraining the model.
Multi-Resolution Support. One key strength of VAR lies in its multi-resolution token maps, which naturally support different output scales. During inference, generation can stop at any intermediate resolution (e.g., \(64 \times 64\), \(128 \times 128\), etc.), offering flexible tradeoffs between quality and speed.
These results validate VAR’s autoregressive transformer as a strong alternative to diffusion- or GAN-based image generators. Its structured, scale-aware approach achieves both fidelity and controllability — setting the stage for broader multimodal extensions and architectural scaling.
Comparison with Other Generative Paradigms To contextualize the significance of VAR’s results, the authors benchmarked it against a wide spectrum of state-of-the-art generative models across four major paradigms: GANs, diffusion models, masked prediction models, and autoregressive (AR) transformers. The below table summarizes the comparison on the ImageNet \(256 \times 256\) class-conditional benchmark. Evaluation metrics include FID (lower is better), Inception Score (IS) (higher is better), and Precision/Recall for semantic and distributional quality, along with model size and inference cost (time).
| Type | Model | FID ↓ | IS ↑ | Pre ↑ | Rec ↑ | #Param | #Step | Time |
|---|---|---|---|---|---|---|---|---|
| GAN | BigGAN [52] | 6.95 | 224.5 | 0.89 | 0.38 | 112M | 1 | – |
| GAN | GigaGAN [273] | 3.45 | 225.5 | 0.84 | 0.61 | 569M | 1 | – |
| GAN | StyleGAN-XL [551] | 2.30 | 265.1 | 0.78 | 0.53 | 166M | 1 | 0.3 |
| Diff. | ADM [122] | 10.94 | 101.0 | 0.69 | 0.63 | 554M | 250 | 168 |
| Diff. | CDM [225] | 4.88 | 158.7 | – | – | 8100M | – | – |
| Diff. | LDM-4-G [531] | 3.60 | 247.7 | – | – | 400M | 250 | – |
| Diff. | DiT-XL/2 [478] | 2.27 | 278.2 | 0.83 | 0.57 | 675M | 250 | 45 |
| Diff. | L-DiT-3B [1] | 2.10 | 304.4 | 0.82 | 0.60 | 3.0B | 250 | >45 |
| Mask. | MaskGIT [77] | 6.18 | 182.1 | 0.80 | 0.51 | 227M | 8 | 0.5 |
| AR | VQGAN [148] | 15.78 | 74.3 | – | – | 1.4B | 256 | 24 |
| AR | ViTVQ-re [743] | 3.04 | 227.4 | – | – | 1.7B | 1024 | >24 |
| AR | RQTransformer [318] | 3.80 | 323.7 | – | – | 3.8B | 68 | 21 |
| VAR | VAR-d16 | 3.30 | 274.4 | 0.84 | 0.51 | 310M | 10 | 0.4 |
| VAR | VAR-d20 | 2.57 | 302.6 | 0.83 | 0.56 | 600M | 10 | 0.5 |
| VAR | VAR-d24 | 2.09 | 312.9 | 0.82 | 0.59 | 1.0B | 10 | 0.6 |
| VAR | VAR-d30 | 1.92 | 323.1 | 0.82 | 0.59 | 2.0B | 10 | 1.0 |
| VAR | VAR-d30-re | 1.73 | 350.2 | 0.82 | 0.60 | 2.0B | 10 | 1.0 |
Key Takeaways.
- VAR sets a new benchmark: It achieves the lowest FID (1.73) and the highest IS (350.2) of any model on ImageNet \(256 \times 256\), surpassing strong diffusion models like L-DiT [1] and GANs like StyleGAN-XL.
- Inference speed is dramatically faster: While diffusion models require hundreds of denoising steps (e.g., 250 for ADM, DiT), VAR completes generation in just 10 autoregressive steps — one per scale.
- Superior precision-recall tradeoff: VAR maintains high recall (0.60) without sacrificing precision, balancing diversity and realism in a way that standard AR models often fail to achieve.
Why VAR Outperforms Traditional VQ-VAE/VQ-GAN Autoregressive Models.
VAR demonstrates significant advantages over raster-scan VQ-based AR models such as VQ-GAN [148], ViT-VQGAN [743], and RQ-Transformer [318], by overcoming both architectural and theoretical limitations. These models typically flatten a 2D grid into a 1D token stream and predict each token sequentially—introducing inefficiencies and violating the natural spatial structure of images.
- Resolution of 2D-to-1D Flattening Issues. Flattening a 2D image into a 1D sequence for raster-order prediction introduces what the authors call a mathematical premises violation. Images are inherently 2D objects with bidirectional dependencies. Standard AR transformers, however, assume strict unidirectional causality, which conflicts with the actual structure of visual data. VAR resolves this mismatch via its next-scale prediction strategy, which operates hierarchically across scales, preserving spatial coherence and reducing unnecessary dependencies.
- Massive Reduction in Inference Cost. While traditional AR models require one autoregressive step per token (e.g., 256\(\times \)256 = 65,536 steps), VAR only needs \(K\) steps (typically \(K = 4\)–\(6\)), since each scale’s token map is generated in parallel. This reduction yields roughly \(O(N^2) \to O(K)\) sequential depth, improving inference speed by over 20\(\times \) in practice compared to VQ-GAN or ViTVQ baselines.
- Enhanced Scalability and Stability. Unlike earlier VQ-based AR models, which often suffer from training instability or limited scaling behavior, VAR exhibits smooth performance scaling with model size and compute. As shown in Table 20.12, the largest VAR variant surpasses both autoregressive and diffusion baselines at scale, demonstrating a power-law-like trend similar to that of large language models (LLMs).
Why VAR Avoids the Blurriness of Traditional VAEs
Standard VAEs often produce blurry images due to the averaging effect in continuous latent spaces and the use of simple L2 reconstruction loss. In contrast, VAR’s multi-scale VQ-VAE circumvents these issues using discrete representations and adversarial objectives:
- Quantized, Discrete Latents. The use of a discrete token space—learned via a shared codebook—eliminates interpolation-based blurriness. At each scale, the image is decomposed into a quantized map \({r}_k\), where tokens correspond to well-defined visual primitives rather than uncertain blends.
-
Residual-Style Encoder and Decoder. Each scale in the encoder captures residual detail not explained by the coarser maps, leading to a more structured and interpretable decomposition. The decoder sums contributions from all scales to reconstruct high-fidelity images with sharp contours and textures.
-
Perceptual and Adversarial Losses. VAR’s VQ-VAE is trained with a compound objective including:
- A perceptual loss \(\mathcal {L}_P\) (e.g., LPIPS) that compares image reconstructions in the feature space of a pretrained CNN like VGG, encouraging realism and sharpness over pixel-wise fidelity.
- An adversarial loss \(\mathcal {L}_G\) that penalizes visually implausible outputs via a GAN-style discriminator, pushing the generator to produce images indistinguishable from real data.
- Hierarchical Representation Enables Coherence. Unlike VQGANs that rely on a single token map, VAR’s hierarchical structure allows different scales to specialize: coarse layers ensure global layout, while fine layers refine details. This structured generation avoids both over-smoothing and oversharpening artifacts common in single-scale VAEs.
Taken together, these innovations allow VAR to combine the sharpness and semantic fidelity of GANs with the training stability and generative flexibility of VAEs—without inheriting their respective downsides.
Scaling Trends, Model Comparison, and Future Outlook VAR [615] demonstrates that coarse-to-fine autoregressive modeling is not only viable, but also highly competitive with, and in many respects superior to, both diffusion models and GANs. Its innovations in architectural design, inference efficiency, and training stability position it as a new standard for high-resolution image synthesis.
Scaling Efficiency and Sample Quality VAR exhibits favorable power-law scaling as model capacity increases. Across multiple variants (e.g., d16 to d30-re), both FID and Inception Score improve steadily, as shown in the below figure. The largest model, VAR-d30-re (2B parameters), achieves an FID of 1.73 and an IS of 350.2 on ImageNet \(256 \times 256\), outperforming L-DiT-3B and 7B, yet requiring only 10 autoregressive steps.
Comparison to Diffusion and Autoregressive Models As detailed in Table 20.12, VAR delivers best-in-class performance across fidelity, semantic consistency, and speed:
- Compared to diffusion models like ADM [122], DiT [478], and L-DiT [1], VAR matches or exceeds sample quality while reducing inference time by over 20×.
- Compared to GANs such as StyleGAN-XL [551], VAR achieves higher precision and recall, while being more stable and easier to scale.
- Most importantly, VAR outperforms previous autoregressive methods (e.g., VQGAN [148], ViT-VQGAN [743], and RQ-Transformer [318]) by resolving their core limitations — primarily the violation of spatial locality introduced by raster-scan decoding.
Qualitative Scaling Effects of VAR To further illustrate the benefits of architectural scaling, the authors created a figure that showcases qualitative samples from multiple VAR models trained under different model sizes \(N\) and compute budgets \(C\). The grid includes generations from 4 model sizes (e.g., VAR-d16, d20, d24, d30) at 3 different checkpoints during training. Each row corresponds to a specific class label from ImageNet [118], and each column highlights progression in visual quality with increasing capacity and training.
As visible in the figure, increased model scale and training compute systematically improve both semantic fidelity (correctness of object structure and attributes) and visual soundness (absence of artifacts, texture realism, and color consistency). For instance, the depiction of ”oscilloscope” and ”catamaran” transitions from ambiguous blobs in early-stage, small models to highly plausible, structurally accurate renderings in larger, well-trained variants.
These qualitative trends corroborate the quantitative findings in Figure 20.139 and Table 20.12, reinforcing that VAR inherits desirable scaling properties akin to large language models: more parameters and compute lead to predictable improvements in generative quality.
Limitations and Future Directions Despite its strengths, VAR still inherits certain limitations:
- Lack of native text conditioning: Unlike diffusion systems such as GLIDE or LDM, VAR has not yet been extended to text-to-image generation. Integrating cross-modal encoders (e.g., CLIP or T5) remains a promising avenue.
- Memory footprint: While more efficient than raster AR models, each scale in VAR still requires full-token parallel decoding, which may challenge memory limits for high-resolution outputs.
- Token discretization ceiling: The reliance on codebook-based representations may bottleneck expressiveness for fine-grained texture, unless dynamic or learned vocabularies are incorporated.
Nonetheless, VAR’s success opens up multiple promising research directions: extending the coarse-to-fine AR paradigm to multimodal transformers, integrating with prompt-based editing, and exploring learned topologies beyond rectangular grids. Its architectural clarity and empirical strength position it as a foundation for the next generation of efficient generative models.
Enrichment 20.11.12: DiT: Diffusion Transformers
Motivation and context Most high-performing diffusion models have used U-Net backbones that combine convolutional biases (locality, translation equivariance) with occasional attention for long-range interactions [122, 531]. The central question addressed by Diffusion Transformers (DiT) [478] is whether a pure Vision-Transformer denoiser operating in latent space can match or surpass U-Net diffusion when scaled. DiT answers in the affirmative: by patchifying VAE latents and processing tokens with transformer blocks modulated via adaptive LayerNorm (adaLN / adaLN-Zero), DiT exhibits clean scaling laws and achieves state-of-the-art ImageNet sample quality at competitive compute.
High-level overview DiT is a standard DDPM/latent-diffusion denoiser \(\epsilon _\theta \) that operates on VAE latents \(z_0=E(x)\in \mathbb {R}^{I\times I\times C}\) (e.g., \(I{=}32\), \(C{=}4\) for \(256^2\) images). With \(q(z_t\!\mid \!z_0)=\mathcal {N}\!\big (\sqrt {\bar \alpha _t}z_0,(1{-}\bar \alpha _t)I\big )\) and \(z_t=\sqrt {\bar \alpha _t}z_0+\sqrt {1{-}\bar \alpha _t}\,\epsilon \), the denoiser predicts \(\epsilon _\theta (z_t,t,c)\) (and a diagonal covariance) by minimizing the usual noise MSE. Class-conditional training uses classifier-free guidance at sampling time.
Why transformers? Intuition. Transformers have appeared repeatedly in earlier parts of this chapter: as attention submodules inside U-Nets, as text encoders, and even as full transformer U-Nets. What distinguishes DiT is the decision to use a pure ViT backbone directly on latent patch tokens, removing convolutional pyramids and skip connections entirely.
This shift yields several concrete benefits that are hard to obtain with U-Nets:
- Global-first context at every depth. Self-attention connects all tokens in all layers, coordinating layout and long-range dependencies continuously, rather than bottlenecking global context at specific resolutions as in U-Nets.
- Simpler, predictable scaling. DiT exposes two orthogonal knobs—backbone size (S/B/L/XL) and token count via patch size \(p\)—so quality tracks forward Gflops in a near-linear fashion. This clarity is difficult with U-Nets whose compute varies non-trivially with resolution and pyramid design.
- Uniform conditioning via normalization. Instead of injecting conditions via cross-attention at a few scales, DiT uses adaLN-style modulation in every block, giving cheap, global, step-aware control without the sequence-length overhead of cross-attention.
- Latent-space efficiency. Operating on VAE latents keeps sequence lengths manageable while retaining semantics. Convolutional U-Nets still pay per-pixel costs that grow with resolution, even in latent space.
In short, transformers are not merely “also used” here; the pure transformer backbone plus compute-centric scaling and adaLN-based conditioning together produce a qualitatively different, more scalable denoiser than a U-Net.
Method: architecture and components
Tokenization (patchify) of the latent. The noised latent \(z_t\in \mathbb {R}^{I\times I\times C}\) is split into non-overlapping \(p{\times }p{\times }C\) patches, each linearly projected to \(d\)-dim tokens with sine–cos positional embeddings. The sequence length is \(T=(I/p)^2\). Reducing \(p\) increases tokens (and Gflops) without changing parameters, acting as a clean compute knob.
High-level overview: DiT as a transformer backbone for diffusion After tokenization, the task is to predict the additive noise on latent patches at diffusion timestep \(t\) (and, optionally, class/text label \(y\)). Diffusion Transformers (DiT) [478] replace the U-Net with a stack of transformer blocks that operate on the patch-token sequence: (i) patchify latents into tokens; (ii) transform them with \(N\) conditional blocks that inject \((t,y)\) at every depth; (iii) project tokens back to per-patch predictions (noise and optionally variance). The motivation is simple: self-attention offers global receptive fields and scales cleanly with depth/width; conditioning via adaptive normalization is cheap and pervasive.
From AdaIN to adaLN: motivation and adaptation Adaptive normalization offers cheap, global control by modulating normalized activations with per-channel scale/shift. StyleGAN’s AdaIN Enrichment 20.6.1 applies \((\gamma ,\beta )\) (from a style code) after InstanceNorm in convnets, broadcasting “style” through every layer with negligible overhead. DiT carries this idea to transformers and diffusion by:
- Swapping InstanceNorm on feature maps for LayerNorm on token embeddings.
- Replacing style latents with diffusion timestep \(t\) and label/text \(y\) as the condition.
- Adding zero-initialized residual gates so very deep stacks start near identity and “open” gradually (stability under heavy noise).
This preserves AdaIN’s low-cost, layer-wise control while fitting the sequence setting and the iterative denoising objective.
DiT block: adaLN and the adaLN-Zero variant The DiT backbone is a sequential stack of \(N\) standard Pre-LN transformer blocks. Each block consumes a token sequence \(X\in \mathbb {R}^{L\times d}\) and applies \[ \mbox{(i) LN} \rightarrow \mbox{MHSA} \rightarrow \mbox{residual},\qquad \mbox{(ii) LN} \rightarrow \mbox{MLP} \rightarrow \mbox{residual}. \] Why this works. MHSA lets every latent patch-token attend to all others, building global spatial coherence; the MLP adds channel-wise capacity after attention has mixed information. Conditioning the LayerNorms lets \(t,y\) shape what MHSA/MLP see—cheaply and pervasively—so early steps favor coarse denoising and later steps focus on fine details.
How conditioning is produced (per-block MLPs, as in DiT). Embed the diffusion timestep and label/text and concatenate to form \(c=\mathrm {Embed}(t,y)\in \mathbb {R}^e\) (sinusoidal \(t\)-embed + learned \(y\)-embed). Each transformer block \(i\) owns a tiny modulation MLP \(g_i:\mathbb {R}^e\!\to \!\mathbb {R}^{6d}\) that outputs six \(d\)-vectors \[ (\gamma _{1,i},\beta _{1,i},\alpha _{1,i},\gamma _{2,i},\beta _{2,i},\alpha _{2,i}) \;=\; g_i(c), \] one triplet for the attention branch (\(k{=}1\)) and one for the MLP branch (\(k{=}2\)). This gives shallow and deep layers different “views” of \((t,y)\) with negligible parameter cost.2
adaLN (adaptive LayerNorm). At each Pre-LN site (before self-attention and before the MLP), replace vanilla LayerNorm by a condition-dependent affine transform: \[ \mathrm {adaLN}_k(X;c)\;=\;\gamma _{k,i}(c)\odot \mathrm {LN}(X)\;+\;\beta _{k,i}(c),\qquad k\in \{1,2\}. \] This injects \((t,y)\) everywhere using only elementwise operations, so the subsequent computations see features already bent toward the current diffusion step and class.
adaLN-Zero (the variant used in practice). DiT’s best-performing blocks add gates on the two residual branches via \(\alpha _{1,i}(c),\alpha _{2,i}(c)\) that are zero-initialized. With \(X\!\in \!\mathbb {R}^{L\times d}\), a full block computes \[ \begin {aligned} Z_1 &= \mathrm {adaLN}_1(X;c), \qquad H \;=\; \mathrm {SelfAttn}(Z_1), \qquad U \;=\; X \;+\; \alpha _{1,i}(c)\odot H,\\ Z_2 &= \mathrm {adaLN}_2(U;c), \qquad M \;=\; \mathrm {MLP}(Z_2), \qquad Y \;=\; U \;+\; \alpha _{2,i}(c)\odot M. \end {aligned} \] Here \(\mathrm {SelfAttn}\) is the standard multi-head scaled dot-product self-attention (MHSA); some figures abbreviate it as “self-attn”. Self-attention lets every token attend to every other (global communication); the multi-head factorization runs several attentions in parallel so different heads can specialize (e.g., shape vs. texture), then concatenates and projects them back to \(d\). Zero-initialized gates make the whole stack start near identity (\(Y\!\approx \!X\)), preventing early instabilities on very noisy inputs; during training the model learns where to “open” attention/MLP paths. Empirically, adaLN-Zero is the variant used for final models; plain adaLN appears mainly in ablations.
Head and parameterization After the final LayerNorm, a linear head maps each token to \(p{\times }p{\times }(2C)\) values (per patch; commonly \(p{=}1\)), then reshapes to the latent grid. The first \(C\) channels parameterize the predicted noise; the remaining \(C\) optionally parameterize a diagonal variance. Across \(T\) denoising steps, DiT iteratively predicts and removes noise to recover a clean latent \(x_0\); a pretrained VAE decoder then converts \(x_0\) to pixels (e.g., \(256{\times }256\) RGB). Intuitively: MHSA builds global structure across patches, the MLP refines channel-wise details, adaLN/Zero injects timestep/class signals at every depth, and the head “de-tokenizes” back to a spatial latent that the VAE upsamples to the final image.
Conditioning and guidance The condition \(c\) is the concatenation of timestep and class/text embeddings. Classifier-free guidance is enabled by randomly replacing the label with a learned “null” embedding during training. At inference, combine unconditional and conditional predictions as \[ \tilde {\epsilon }\;=\;\epsilon _{\emptyset }\;+\;s\,(\epsilon _{y}-\epsilon _{\emptyset }),\qquad s>1, \] steering samples toward the target class/text. Among conditioning routes (in-context tokens, cross-attention, adaLN, adaLN-Zero), adaLN-Zero consistently converges fastest and achieves the best FID with negligible overhead; cross-attention is more flexible for long text but typically adds \(\sim 15\%\) compute.
Training objective and setup DiT trains end-to-end in latent space with the standard denoising objective. For VAE-encoded images \(x_0\), noise \(\epsilon \!\sim \!\mathcal {N}(0,I)\), timestep \(t\), and condition \(y\), \[ \mathcal {L} \;=\; \mathbb {E}_{x_0,\epsilon ,t,y}\Big [\;\big \|\epsilon \;-\; \hat {\epsilon }_\theta (x_t,t,y)\big \|_2^2\;\Big ], \quad x_t \;=\; \sqrt {\bar {\alpha }_t}\,x_0 \;+\; \sqrt {1-\bar {\alpha }_t}\,\epsilon . \] Classifier-free guidance is enabled by dropping \(y\) with some probability during training and learning a null embedding. In practice, AdamW with cosine LR decay and a brief warm-up are used; adaLN-Zero’s identity start helps avoid early instabilities in deep attention stacks while maintaining the capacity benefits of transformers.
Experiments and ablations
Scaling and SOTA comparisons. Compute-centric scaling is the core story. DiT exposes two orthogonal axes: backbone size (S/B/L/XL) and token count via patch size (\(p\!\in \!\{8,4,2\}\)). Increasing either axis improves FID at fixed training steps; the best results combine large backbones and small patches.
Training-time scaling trends. Holding \(p\) fixed and increasing backbone (S\(\rightarrow \)XL) lowers FID throughout training; holding backbone fixed and decreasing \(p\) (more tokens) also lowers FID. The separation between curves indicates robust compute-to-quality scaling across 12 configurations.
Qualitative scaling: more flops \(\rightarrow \) better images. A large grid sampled at 400K steps from the same noise and label shows that increasing transformer Gflops—either via larger backbones or more tokens—improves visual fidelity. Left-to-right increases backbone size; top-to-bottom decreases patch size (more tokens).
Gflops predict FID. Across all 12 DiTs at 400K steps, transformer forward Gflops strongly correlates with FID (reported correlation \(\approx \!-0.93\)). This metric predicts quality better than parameter count and makes design trade-offs explicit.
Total training compute vs. FID. Plotting FID against total training compute shows smooth, near power-law improvements. Larger models form a lower envelope: for the same train compute, bigger models reach better FID than smaller ones trained longer.
Sampling compute cannot replace model compute. Increasing denoising steps improves quality for each model, but small models cannot catch large ones even with more sampling steps (higher inference Gflops). For a fixed sampling budget, it is typically better to deploy a larger DiT at fewer steps than a smaller DiT at many steps.
Benchmark summary (ImageNet 256/512). On ImageNet-256, DiT-XL/2 with classifier-free guidance (scale \(\approx \)1.5) attains FID \(\approx \) 2.27, sFID \(\approx \) 4.60, and IS \(\approx \) 278, exceeding LDM and ADM variants. At 512, DiT maintains strong results with FID \(\approx \) 3.04. Precision/Recall indicate balanced fidelity/diversity relative to GAN and diffusion baselines. (Exact tables are in [478]; summarized here for brevity.)
What changed vs. Stable Diffusion and why it matters
- Backbone. U-Net (ResNet blocks + spatial attention at select scales) \(\Rightarrow \) pure ViT over patch tokens. DiT’s global-first attention coordinates layout at all depths; no hand-crafted multi-scale pyramid or skip connections are required.
- Conditioning. Cross-attention to text (costly, sequence-length dependent) \(\Rightarrow \) adaLN / adaLN-Zero (cheap, global, step-aware). This adapts AdaIN-style modulation (Enrichment 20.6.1) to LayerNorm, distributing conditioning throughout the network with near-zero overhead and superior FID (see Figure 20.144).
- Scaling lens. Params and resolution-dependent conv costs \(\Rightarrow \) forward Gflops as the primary metric. As shown in Figure 20.148, Gflops strongly predicts FID and guides trade-offs between model size and token count.
-
Compute knobs. Channel/width heuristics and UNet depth \(\Rightarrow \) orthogonal knobs (backbone size S/B/L/XL and patch size \(p\)). Figures 20.145–20.147 demonstrate monotonic quality gains along both axes.
- Variance head. DiT’s head predicts noise and a diagonal covariance per spatial location, enabling variance-aware denoising in latent space.
Outcome. At similar or lower compute, DiT matches or surpasses U-Net diffusion on ImageNet, and scales predictably (quantitatively in Figure 20.148, Figure 20.149; qualitatively in Figure 20.147).
Relation to prior and follow-ups AdaIN-based control in StyleGAN1 (Enrichment 20.6.1) motivated normalization-as-conditioning; DiT shows a transformer-native realization (adaLN-Zero). Subsequent work such as L-DiT [1] scales DiT further in latent space, reporting even stronger ImageNet results. DiT complements latent U-Nets [531]: both benefit from classifier-free guidance and VAE latents, but DiT offers LLM-like scaling and a simpler global-context story.
Limitations and future work
- Memory/latency at small \(p\). Reducing \(p\) increases tokens \(T\) and attention memory quadratically in \(I\); efficient attention, sparse routing, or hierarchical tokenization are promising.
- Inductive bias. Removing convolutions removes explicit translation equivariance and pyramids; hybrid conv–transformer blocks or relative position biases may improve data efficiency.
- Long-sequence conditioning. Cross-attention for long text is flexible but adds compute; extending adaLN-style modulation to long sequences or hybridizing with lightweight cross-attention is an open avenue.
Practical recipe Train in latent space with a strong VAE. Pick DiT-B/L/XL by budget. Start at \(p{=}4\), drop to \(p{=}2\) if memory allows. Expect monotonic FID gains by increasing backbone size and tokens (Figure 20.146, Figure 20.148). Prefer a larger DiT with fewer steps over a smaller DiT with many steps for a fixed sampling budget (Figure 20.150).
1Parti [110] is a proprietary Google model that produces images autoregressively from discrete tokens. Because its code and training details are not public, and its autoregressive design differs from the diffusion focus of this chapter, we do not discuss Parti further.
2An equivalent implementation shares a trunk MLP across blocks and uses per-block linear heads to project into \((\gamma ,\beta ,\alpha )\); the official DiT code uses per-block modulation MLPs.